n1

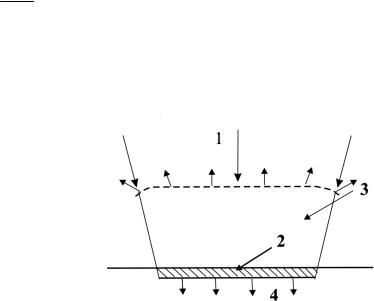
21

что жидкость не нагревается выше критической температуры, можно оценить из соотношения:

p mvи ,и2 rv

где m — испаренная масса, и , — время установления процесса испарения, v

— скорость движения волны сжатия, r — расстояние от поверхности, vи — скорость истечения пара.

Рис. 1.5. Схема процесса возбуждения звука в жидкости при ее испарении с поверхности за счет поглощения лазерного излучения: 1 —лазерный пучок; 2 — испаряемый объем; 3 — разлетающийся пар: 4 — волна сжатия в жидкости

Очевидно, энергия световой волны, перешедшая в энергию звуковой волны, растет при увеличении поглощения световой волны в среде. Поэтому коэффициент трансформации максимален при оптическом пробое.

Другой механизм возбуждения звуковых волн в среде основан на вынужденном рассеянии Мандельштама-Бриллюэна (ВРМБ), т.е. явлении рассеяния световых волн на тепловых упругих волнах (см. раздел 3).

При любом механизме генерация акустических волн, как за счет локального нагревания и испарения, так и за счет вынужденного рассеяния на неоднородностях показателя преломления, звуковая волна может сама по себе приводить либо к разрушению среды, если амплитуда звуковой волны больше предела упругости материала, либо к уменьшению интенсивности поглощенного лазерного потока вследствие перекачки его энергии в звуковые колебания среды.

К появлению механических напряжений в материале может привести его неравномерное нагревание. Это обусловлено свойством тел увеличивать свой объем при нагревании. Напряжения тем больше, чем больше перепад температур, возникающий при локальном нагревании материала, чем больше его коэффициент термического расширения.

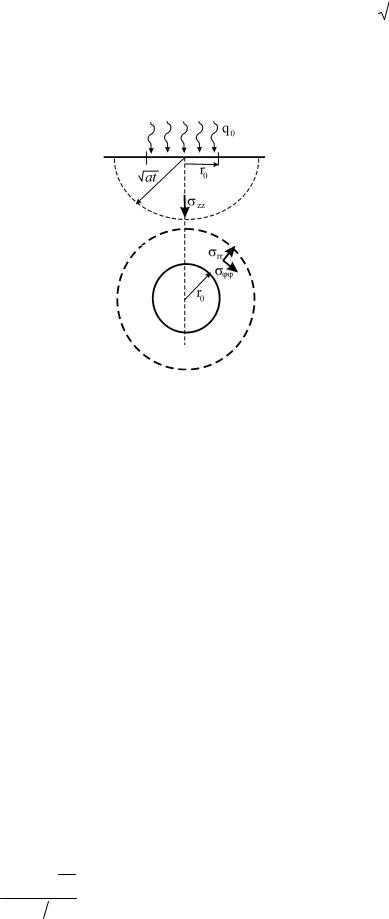
Напряжения, возникающие при локальном лазерном нагревании можно характеризовать тензором напряжений. В цилиндрической системе координат (см. рис. 1.6) его нормальные компоненты - zz . rr и . Сжимающие напря-

жения отрицательны, растягивающие – положительны. В первом приближении можно считать, что при локальном нагревании напряжения zz сжимающие

предел прочности обычно для растягивающих напряжений меньше, то наиболее опасными являются напряжения , которые вне области воздействия поло-

жительны.

Рис. 1.6. Напряжения, возникающие при локальном нагреве.

При локальном разогреве за счет теплового расширения поверхность внутри области воздействия радиуса r0 представляет собой выпуклую сферу с радиусом:

0,2?0,5 – коэффициент Пуассона. Оценка радиуса кривизны деформированной поверхности показывает, что при r0 ~0,1 см, 0,5 15см.

Такая локальная деформация поверхности может приводить к изменению индикатрисы отражения зеркал при наличии неоднородностей отражения.

Пусть на поверхности зеркала с поглощательной способностью A0 есть неоднородность радиуса r0 с поглощательной способностью A1 A0 . Температуру поверхности зеркала внутри неоднородности можно оценить как температуру, до которой нагреется полупространство с поглощательной способностью поверхности A0 при действии равномерно распределенного лазерного потока с плотностью мощности q0 (см. раздел 1.3.2) плюс температура локального перегрева неоднородности Tлок :

T( x 0 ) 2q0 A0 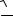at Tлок

S

23

Перегрев неоднородности можно оценить как температуру, до которой нагреется малая область радиуса r0 при действии поглощенного потока

(A1 A0 )q0

Tлок q0 A1 A0 r0

S

Относительный перегрев неоднородности составит

T A1 A0 r0 ,

при A1 1 относительный перегрев будет:

При малых значениях A0 , что характерно для зеркал, перегрев может достигать значительных величин (десятки раз).

1.2.2. Фазовые переходы в твердом состоянии (лазерное упрочнение)

Известно, что при нагревании твердых тел, в них могут происходить различные изменения структуры, так называемые структурно-фазовые переходы. Поскольку воздействие световых потоков большой мощности сопровождается ростом температуры материала, очевидно, что лазерный разогрев вещества при определенных условиях также может привести к инициации структурнофазовых изменений. При быстром охлаждении, которое характерно для лазерного воздействия, обратный переход, как правило, успевает произойти не полностью, происходит «замораживание» (закалка) высокотемпературных состояний. Кроме того, могут быть реализованы: кристаллизация аморфизированных при ионной имплантации полупроводников, аморфизация поверхности металлов (образование металлических стекол) при сверхбыстром охлаждении расплава при лазерном воздействии, упрочнение металлов за счет ударной волны, возникающей при наличии импульса отдачи.

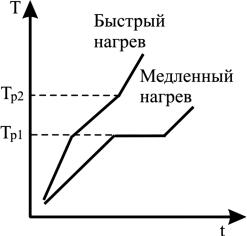
При медленном нагреве структурно-фазовый переход происходит при определенной температуре Tp . При быстром лазерном нагревании такой переход

происходит в некотором диапазоне температур Tp1 T Tp2 (см. рис. 1.7).

Как известно из теории структурно-фазовых переходов, они проходят в две стадии: образование зародышей новой фазы с размером большим критического, когда они становятся устойчивыми, и рост этих зародышей за счет диффузионного присоединения атомов к новой фазе.

Скорость образования зародышей критического размера определяется выражением

Vb V0b exp Fb Gb .kT

24

Fb - энергия перехода молекулы из исходной фазы на поверхность зародыша новой фазы, V0b - постоянная, Gb - энергия Гиббса образования зародыша критического размера, k - постоянная Больцмана.

Рис. 1.7. Смещение критической точки Tp при быстром нагреве.

Скорость роста кристаллов новой фазы, которая определяется диффузионным переходом молекул из исходной фазы в новую, подчиняется закону:

Fk - энергия активации диффузии молекулы из исходной фазы в зародыш, V0k

- постоянная, Gp - энергия Гиббса роста кристаллов.

Скорости образования и роста зародышей имеют максимумы при различных температурах (температура, при которой скорость образования зародышей максимальна, меньше температуры максимальной скорости роста зародышей).

При закалке сплавов (сталей, латуней, бронз и т.п.), когда высокотемпературные фазы отличаются от низкотемпературных главным образом соотношением компонентов, определяющей стадией перехода является диффузионный рост образовавшихся на предварительном этапе или уже существовавших зародышей новой фазы.

Обычно анализ структурно-фазовых переходов проводят по изотерме температуры перехода, отвечающей переходу при стационарном нагревании или изотерме Tp2 . Рассматривают температурное поле, возникающее в мате-

риале при лазерном нагревании. При этом считают, что термоупрочнение происходит в той области термического влияния, где температура окажется выше температуры Tp1 или Tp2 . При этом считается, что скорость остывания доста-

точно велика для того, чтобы образовавшиеся высокотемпературные структуры не успели разрушиться.

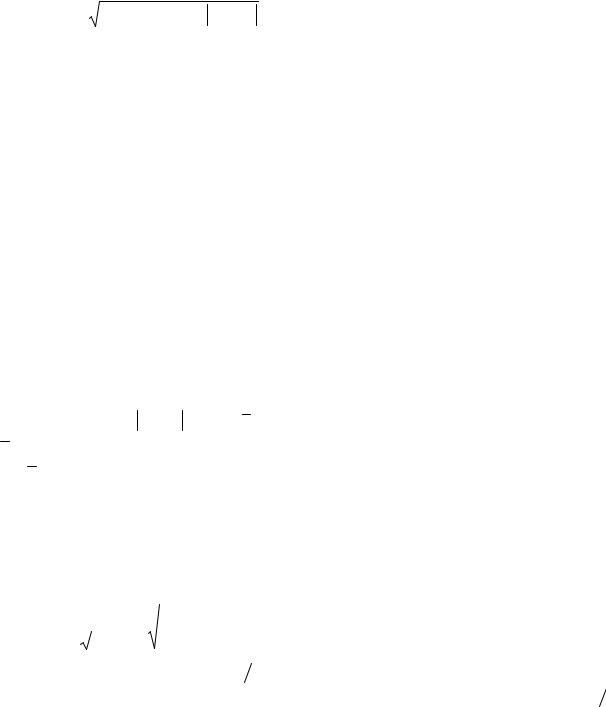
26

щадка с распределением температуры f (r / r0 ). Из (1.17) получаем следующее выражение для reff :

Из выражения (1.18) следует, что лишь малая часть освещенного пятна вносит заметный вклад в термоэлектронную эмиссию, причем площадь этой «рабочей» части изменяется со временем пропорционально Te (0,t) . Сложная форма реальных импульсов требует обычно использования численного интегрирования для расчета Te (0,t) .

Следует отметить обстоятельство, которое может оказаться существенным при изучении термоэлектронной эмиссии под действием лазерного излучения. Формула (1.16), используемая обычно для расчета тока эмиссии, выведена в предположении, что электронный газ однородно нагрет до температуры Te . В рассматриваемых условиях это предположение неточно, поскольку в металле, поглощающем мощное излучение, возникает вблизи поверхности значительный градиент температуры, который вызывает в свою очередь возникновение электронного тока. Расчет, уточняющий выражение (1.16) показывает, что добавка к току, связанная с градиентом температуры, мала. Уменьшение тока термоэлектронной эмиссии определяется наличием градиента температуры, направленного к поверхности металла. Так например, относительная величина поправки к току для меди составляет примерно

J / J ~ 3 10 8 T / x 3 10 8 q / e

(q среднее за импульс значение плотности потока лазерного излучения), что при q ~ 107 Вт/см2 дает около 10%.

Особенность фотоэлектрического эффекта под действием лазерного излучения состоит в том, что в практически важных случаях энергия кванта оказывается меньше потенциала ионизации, так что выход электрона из металла происходит при поглощении нескольких квантов.

Для этого случая плотность тока j равна

Как уже отмечалось, ток, обусловленный многофотонным фотоэффектом, сравнительно трудно наблюдать, поскольку он маскируется термоэлектронной эмиссией. Один из способов преодоления этой трудности состоит в уменьшении длительности лазерного импульса. Поскольку ток термоэлектронной эмиссии несколько запаздывает относительно потока излучения, а фотоэффект является практически безынерционным, возможно раздельное наблюдение этих эффектов. Для наблюдения фотоэффекта следует выбирать режимы облучения,

27

когда температура поверхности мала, например, для серебра температура поверхности за время импульса должна повысится приблизительно на 250 °С, что исключает разрушение поверхности и обусловливает очень малую величину термоэмиссионного тока.

1.2.4. Основные особенности лазерной активации процессов аррениусовского типа

При лазерном нагреве материалов на их поверхности могут инициироваться различные реакции, скорость которых растет с температурой по активационному закону (закону Аррениуса), например реакции окисления, разложения, нитрирования, карбидизации др. Большие скорости изменения температуры, реализуемые при лазерном воздействии, определяют особенности протекания этих процессов по сравнению с изотермическими условиями. Рассмотрим их на примере лазерного окисления металлов и полупроводников.

При построении физических моделей и теории лазерного окисления исходят из представлений, сформированных в результате исследований обычного, изотермического гетерогенного окисления поверхности с образованием твердых окисных пленок.

Процесс окисления включает в себя несколько стадий: адсорбцию кислорода на поверхности, связывание свободных электронов металла или растущего окисла, диффузию и электроперенос ионов металла и кислорода по вакансиям, междоузлиям и другим дефектам сквозь слой продукта реакции к межфазным границам и собственно химическую реакцию с образованием нового слоя окисла. В тонких окисных слоях (b 50 500 A; здесь b — толщина окисла) сильное влияние на кинетику окисления может оказывать электрическое поле, возникающее вследствие появления контактной разности потенциалов между окислом и металлом, и локализации электронов на границе окисел–газ на поверхностных энергетических уровнях хемосорбированного кислорода. Для окислов толщиной до 100 A, в которых можно пренебречь объемным зарядом, это поле существенным образом снижает энергию активации диффузии ионов, если энергия, приобретенная ионом от поля на пути в одну постоянную решетки окисла, оказывается гораздо больше тепловой. В результате скорость окисления металла заметно возрастает. По мере увеличения толщины окисла электрическое поле, связанное с разделением зарядов вблизи контактных границ с металлом и газовой фазой, постепенно экранируется объемным зарядом. Критериальным параметром здесь выступает дебаевская длина экранирования ld , со-

ставляющая ~ 0.1 мкм при температуре 1000 К и концентрации заряда n0 ~ 1015 см–3 или 0,01 мкм при n0 1017 см–3. Для окислов толщиной b ld основным механизмом переноса ионов становится диффузия.

Законы окисления могут существенно отличаться как для различных металлов, так и для конкретного металла в зависимости от толщины окисла, температуры, давления кислорода. При этом, как и вообще в химической кинетике, скорость окисления в каждой ситуации определяется скоростью его самой медленной (лимитирующей) стадии. В большом числе случаев кинетику изотерми-

28

ческого окисления металла можно описать обобщенным активационным законом вида

где t – время; Bm – некоторая константа; Ta – выраженная в Кельвинах энергия активации лимитирующей стадии реакции (обычно Ta 1 5 104 К), m и n – параметры. При различных m и n из уравнения (1.20) следуют известные законы окисления. В частности, при m 0, n 0 выражение (1.20) соответствует линейному окислению, лимитируемому процессом перехода ионов металла через контактную границу с окислом; при этом Ta V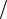k0 , где V — высота граничного потенциального барьера. При m 0, n 2 выражение (1.20) описывает линейный закон окисления, которому подчиняется первоначальный рост окисла, лимитируемый термоэлектронной эмиссией из металла; в этом случае Ta e 01 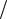k0 , где e — работа выхода электрона из металла, 01 — энергия электронного сродства окисла. При m 1 обобщенный закон окисления переходит в уравнение Мотта, если n 1, и Вагнера, если n 0, которые соответствуют параболическим законам изотермического окисления, контролируемого диффузионными процессами. При m 2 уравнение дает кубический закон окисления, когда лимитирующей стадией реакции является диффузия ионов сквозь слой объемного заряда в окисле. Таким образом, уравнение (1.20) формально обобщает многие конкретные законы окисления. Исключение составляют случаи, когда скорость реакции определяется туннелированием электронов из металла к кислороду сквозь слой растущего окисла или притоком кислорода из газовой фазы.

Наиболее общей особенностью лазерного окисления, независимо от длины волны используемого излучения и длительности воздействия, является неизотермичность реакции. Если окисная пленка не влияет на оптические свойства металла, то для построения простейшей феноменологической теории лазерного окисления необходимо найти временной закон, по которому изменяется температура окисляющейся поверхности T t , и ввести его в общее решение уравнения (1.20):

bm 1 Bm m 1 In t b0m 1 ,

где b0 — начальная толщина окисной пленки. Такой подход фактически означает, что микрокинетика лазерного и изотермического окисления идентичны.

При вычислении In t следует учесть, что во всех представляющих интерес случаях реальная температура металла T t остается значительно меньше температуры активации Ta , T TH TH2 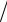Ta ~ 100 (где TH — начальная температура). Поскольку при T t Ta активационная экспонента резко растет с температурой, основной вклад в In t вносят лишь те моменты времени, когда

29

температура близка к максимальной. Поэтому процесс неизотермического окисления по своему результату эквивалентен изотермическому окислению при максимальной (на данном временном интервале) температуре, которая поддерживается в течение некоторого «эквивалентного» времени te . При этом te определяется поведением функции T t вблизи ее максимального значения TM .

Если внутрь промежутка (0,t ) попадает максимум температуры TM , достигаемый в некоторый момент t0 , причем скорость изменения температуры в этот момент претерпевает разрыв, то

В этом случае формулы (1.23) и (1.24) описывают полную толщину окисной пленки за весь цикл нагрев–остывание. Как видно из уравнений (1.22–1.24), в рассмотренном приближении время te не зависит от параметра n .

При наличии на кривой T t нескольких максимумов температуры (например, когда металл нагревается серией световых импульсов) как следует из (1.21), полное эквивалентное время изотермической реакции равно сумме этих времен, вычисленных для каждого из максимумов.

Одним из следствий, вытекающих из рассмотренных закономерностей лазерного окисления, является зависимость скорости неизотермической реакции ( S ) от темпа нагрева металла при m 0. В этом нетрудно убедиться, если подставить в исходное уравнение (1.20) его решение

с учетом зависимости te от температуры и скорости ее изменения (1.22). В итоге для наиболее типичного случая (m 1, n 0) получим:

30

Видно, что скорость окисления при температуре T тем больше, чем выше скорость нагрева металла T t . Такая особенность представляет интерес потому, что от скорости окисления зависит его экзотермичность, обусловленная выделением теплоты образования окисла G . Оценки и эксперимент показывают, что при нагреве термически тонких пластин из металлов с большим тепловым эффектом реакции окисления до некоторой граничной температуры, плотности потока, выделяемого при реакции qr Gs , может оказаться достаточно для продолжения разогрева после окончания импульса. Например, при нагреве ти-

Быстрый разогрев может служить также причиной структурных отличий окисных пленок, получаемых при лазерном воздействии. Это связано как с возникновением заметных термонапряжений в системе окисел–металл, так и с тем, что на поверхности металла не успевает образоваться промежуточный подслой низкотемпературных окислов.

Наряду с быстрым нагревом, при лазерном воздействии происходит быстрое остывание материала. Это характерно, в первую очередь, для массивных металлов, температура поверхности которых после окончания импульса заметно уменьшается за время порядка tи . В таких условиях на поверхности могут сохраниться высокотемпературные (как правило, неустойчивые) высшие окислы, которые при медленном охлаждении распадаются. Так, при исследовании методом электронной спектроскопии состава окисла на пленке хрома, нагретой на воздухе импульсами излучения длительностью 10 нс, одновременно с обычной двуокисью хрома Cr2O3 обнаруживается высший окисел CrO3.

1.2.5. Диффузионно-химические явления

При нагреве многих металлов в кислороде или на воздухе, наряду с окислением, происходит частичная диффузия и растворение кислорода в приповерхностных слоях металла. Поскольку диффундирующие атомы представляют собой дополнительные центры рассеяния для электронов проводимости, а растворение кислорода сопровождается перестройкой электронной структуры металла, то в результате изменяются как частота столкновений , так и плазмен-

ная частота p свободных электронов, и, следовательно, поглощательная спо-

собность металла.

Существенно, что активация процесса диффузии происходит при более низких температурах, чем окисление, а для проявления его влияния требуется сравнительно малое время. Это связано с тем, что для возникновения изменений поглощательной способности достаточно, чтобы диффузия и растворение кислорода произошли в скин–слое, толщина которого для видимого и ИК– излучения не превышает 10–6 –10–5 см. В изотермических условиях время td ,

необходимое для этого, определяется большим из времен - 2 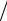D T (характер-