
n1
.pdf
121
- ионизация нейтральных атомов ускоренными электронами, т. е. реакция A e A e e , в результате которой происходит размножение свободных электронов;
- развитие электронной лавины.
Эти явления не происходят строго последовательно, наоборот, как будет видно в дальнейшем, в значительной мере они происходят одновременно. Однако целесообразно рассмотреть эти явления независимо, указав также и на их взаимосвязь во времени. Обратимся к рассмотрению основных свойств этих явлений.
Следует отметить, что начальное число свободных электронов в области фокусировки излучения в газе может быть весьма мало.
В принципе, для развития электронной лавины достаточно одного начального свободного электрона. Поэтому речь идет о единицах свободных электронов в области фокусировки, то есть о начальной плотности свободных электронов порядка ne0 ~ 108 см-3. Эта величина гораздо больше естественной плотности свободных электронов в газе из-за ионизации газа космическими частицами и естественной радиоактивностью. Однако это число гораздо меньше концентрации примесей с малым потенциалом ионизации (в первую очередь
– углеводородных молекул). Свободные электроны образуются в результате многофотонной ионизации атомов этих примесей. Ввиду малого потенциала ионизации (5 – 6 эВ) степень нелинейности при этом не велика и ионизация происходит с большой вероятностью в относительно слабых полях.
3.1.1.1. Многофотонная ионизация
Многофотонное возбуждение представляет собой процесс, в котором электрон в квантовой системе (в атоме, молекуле) переходит из одного (начального) связанного состояния в другое (конечное) связанное состояние в результате поглощения нескольких фотонов действующего излучения. Многофотонное возбуждение противоположно ступенчатому или каскадному возбуждению, когда поглощение каждого последующего фотона переводит квантовую систему из одного связанного состояния в другое (более высокое) связанное состояние. Принципиальная возможность многофотонного перехода электрона из одного связанного состояния в другое (связанно-связанный переход) обусловлена соотношением неопределенности энергия — время. Согласно этому соотношению закон сохранения энергии для промежуточных (виртуальных) состояний может не выполняться; он выполняется лишь для начального и конечного состояний.
При однофотонной фотоионизации атом или молекула вещества ионизуется при столкновении с фотоном. При этом процесс прямой ионизации возможен при выполнении законов сохранения энергии и импульса
|
1 |
m 2 |
1 |
M |
0u2 |
1 |
mu2 |
|
|
||
|
|
2 |
|
|
|
||||||
2 |
|
|
|
2 |
|
, |
(3.1) |
||||
|
|
|
|
|
|
|
|
||||
|
|
i mv M0u |
|
|
|||||||
|
|
c |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||

122
где i единичный вектор, определяющий начальное направление распространения лазерного излучения (направление движения фотонов), m, v – масса и скорость электрона, M0 , u - масса и скорость иона. Из-за выполнения условия M0 m, , и практически вся энергия фотона передается электрону. Про-
цесс фотоионизации может происходить непосредственно (прямой механизм) h M M e
или через промежуточное состояние (косвенная фотоионизация) h M M*
M* h M e ,
где M , M *, M — обозначает нейтральный, возбужденный, ионизированный атом.
Вероятность p многофотонной ионизации в единицу времени зависит как от эффективного поперечного сечения многофотонной ионизации k , так и от интенсивности лазерного излучения (плотности фотонов) J
p ,J k J k |
(3.2) |
|
( k – степень нелинейности, k |
||
I h 1 , I – потенциал ионизации). |
Процессы многофотонной ионизации не являются пороговыми процессами по интенсивности (3.2) поскольку вероятность многофотонного возбуждения имеет конечную величину при сколь угодно малой интенсивности излучения, однако, образование плазмы критической плотности за счет многофотонной ионизации атомов газа является пороговым процессом по интенсивности излучения. Действительно, для того, чтобы процесс ионизации вещества стал развиваться, необходимо достичь определенной критической nкр степени иони-
зации, при которой возникает положительная обратная связь по поглощению. При фиксированной плотности газа n для достижения значения nкр необ-
ходима определенная степень ионизации Ne |
Na , т. е. определенная полная ве- |
||||
роятность ионизации W, определяемая как |
|
||||
|
Ne |
p ,J л |
ne |
, |
(3.3) |
|
Na |
|
|||
|
|
n |
|
||
где Na , Ne – полное число атомов и электронов в облучаемой зоне, л – время действия лазерного излучения на вещество, ne – плотность свободных электронов.
Из соотношения (3.3) видно, что при фиксированных л , плотности вещества и заданной плотности свободных электронов ne соответствует определенная пороговая интенсивность J . Следует отметить, что соотношения (3.2) и (3.3) позволяют оценить пороговую интенсивность возникновения оптического пробоя лишь с учетом многофотонной ионизации. Величины, рассчитанные по (3.3), приблизительно на порядок превышают экспериментально полученные значения. Это означает, что нелинейная ионизация не является основной причиной образования плотной плазмы.
123
В тех случаях, когда плотность газа или длительность лазерного импульса малы, за счет ионизации образуется малое число свободных электронов. Если мала область фокусировки лазерного излучения, то образовавшиеся свободные электроны успевают покинуть область воздействия – их концентрация не достигает критического значения. Для этих условий должен существовать другой механизм ионизации газа.
3.1.1.2. Лавинная ударная ионизация
Кроме нелинейной ионизации нейтральных атомов в поле излучения происходит процесс ионизации атомов при их столкновении с электронами, ускоренными в поле излучения. Образование плазмы за счет электронной ионизации при фиксированной напряженности поля излучения может произойти с большей вероятностью, чем процесс нелинейной ионизации. Лавинная ионизация приведет к оптическому пробою только в том случае, когда результирующая скорость размножения электронов настолько велика, что превышает пороговое значение, необходимое для образования плазмы в течение лазерного импульса. Так как скорость набора энергии электронами пропорциональна интенсивности лазерного излучения, а скорость потерь практически не зависит от поля, то при заданной длительности лазерного импульса должно существовать пороговое значение интенсивности лазерного излучения, по достижении которого возникает лавинная ионизация.
Электронная ионизация, ведущая к образованию плазмы, происходит при соударении свободных электронов с нейтральными атомами. Она доминирует при больших значениях N, л и значительных размерах области фокусировки лазерного пучка.
Кинетическая энергия подавляющего большинства свободных электронов, образующихся при многофотонной ионизации атомов и молекул,кин K I , где K – число фотонов, поглощение которых необходимо для выполнения закона сохранения энергии. Таким образом, в видимом диапазоне частот кин 1 эВ. Поэтому свободные электроны, образованные в газе, не могут ионизовать атомы газа, потенциалы ионизации которых на порядок величины больше.
Количественное описание рассмотренных процессов, приводящих к оптическому пробою, затруднено, особенно если необходимо учесть квантовую природу лавинной ионизации. Мы ограничимся простой классической моделью.
Предположим, что возникновение первичных электронов и их лавинное размножение это два последовательных независимых процесса. Если первичные электроны создаются в процессе n-фотонной ионизации, то их плотность
(3.4)
где I интенсивность излучения лазера, а параметр G пропорционален длительности лазерного импульса.
Предположим также, что процесс умножения числа электронов начинается со значения электронной плотности 0 . Пусть скорость ионизации, a g
124
скорость потерь, тогда результирующая скорость размножения электронов равна
|
dρ |
(η g)ρ , |
(3.5) |
|
|
||
|
dt |
0 |
|
|
|
|
|
откуда |
|
|
|
ρ(t) ρ0exp[(η g)t]. |
(3.6) |
||
Для наступления оптического пробоя величина должна достичь крити- |
|||
ческого значения кр (порядка |
108 см 3), соответствующего начальной стадии |
||
образования плазмы в течение лазерного импульса. Если длительность лазерного импульса равна i , то порог оптического пробоя характеризуется пороговой скоростью ионизации . Заметим, что величина пропорциональна I , а скорость потерь g от интенсивности I не зависит. Следовательно, наличие кр оз-
начает, что существует пороговое значение интенсивности |
Iкр , при которой |
||
возникает пробой. Из (3.6) получаем |
|
||
ηкр g τi 1 ln |
ρкр |
. |
(3.7) |
|
|||
|
ρ0 |
|
|
Чтобы теперь найти соотношение между кр и Iкр , воспользуемся класси-
ческой моделью свободного электрона.
Увеличение энергии электрона может происходить при столкновениях свободного электрона с атомами газа. Двигаясь в поле силового центра (ядро атома) в отсутствие внешнего поля, свободный электрон теряет кинетическую энергию на излучение (тормозное излучение, тормозной эффект). В присутствии сильного внешнего поля тормозной эффект носит вынужденный характер, это так называемый вынужденный тормозной эффект. В присутствии внешнего поля электрон может увеличивать свою кинетическую энергию за счет внешнего поля (антитормозной или обратный тормозной эффект). В обоих случаях законы сохранения энергии и импульса могут быть выполнены за счет взаимодействия электрона с третьим телом – атомом. Отметим, что речь идет об упругих столкновениях, то есть о столкновениях, в которых внутренняя структура атома не изменяется.
Используя принцип детального равновесия Эйнштейна для излучения, можно показать, что в данном случае имеет место равенство
(3.8)
в котором B12 и B21 – коэффициенты Эйнштейна для поглощения и испускания излучения. В соотношении (3.8) кин , v — кинетическая энергия и скорость электрона до соударения с атомом, кин , v — после соударения. Положим, что при соударении электрон поглощает квант внешнего поля так, что E E . а v E 1 2 . Тогда, согласно (3.8), можно записать соотношение между коэффициентами поглощения и вынужденного испускания излучения:
2 . Тогда, согласно (3.8), можно записать соотношение между коэффициентами поглощения и вынужденного испускания излучения:

|
|
|
|
|
|
|
125 |
|
B12 |
(E) |
|
v |
|
E 1 2 |
|
||
|
|
|
|
|
|
. |
(3.9) |
|
B21(E ) |
v |
E |
||||||
|
|
|
|
|||||
Из (3.9) видно, что преобладает вынужденное поглощение, причем тем сильнее, чем меньше энергия электрона E . Таким образом, процесс изменения энергии электрона в большом числе последовательных столкновений с атомами представляет собой ряд последовательных актов поглощения-излучения энергии, в результате которых энергия электрона постепенно увеличивается.
Скорость набора энергии электроном определяется уравнением
|
dW |
qe2 |
|
E |
|
2 τ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
m ( 1 2 τ2 |
|
|
|
|
||||||
|
dt |
) |
|
|
|
|||||||
|
|
|
e |
|
|
|
|
|
||||
где E амплитуда электромагнитной волны с частотой |
, |
|
характерное |
|||||||||
время между столкновениями, сопровождающимися передачей импульса, qe и me заряд и масса электрона соответственно. Если энергия ионизации атомов или молекул равна WI , то скорость ионизации определяется соотношением
η |
|
|
q2 |
|
E |
|
2 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
e |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
m W ( 1 |
|
2 τ2 |
) |
|
|
|
|||||||
|
|
e |
I |
|
|
|
|
|
|
||||
Из (3.7) (3.10) получим |
|
|
|
||||||||||
|
|
me cWI( 1 2 τ2 ) |
1 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Iкр |
|
|
2πq2 τ |
|
|
τ |
|
ln |
|||||
|
|
|
|
g |
i |
||||||||
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
(3.10)
ρ |
кр |
|
|
|
|
|
(3.11) |
||
ρ |
||||
. |
||||
|
0 |
|
|
|
Последнее соотношение позволяет в явной форме установить, как порог пробоя зависит от различных физических параметров.
Как мы уже отмечали, при заданной плотности вещества оптический пробой наступает при определенном пороговом значении плотности потока лазерного излучения (см. 3.2). Однако это связано не с процессами, приводящими к ионизации, так как вероятность многофотонной ионизации в единицу времени (3.2) не зависит от интенсивности излучения, а с процессами возбуждения атомов.
Основное уравнение, описывающее развитие электронной лавины, можно представить в виде
Ne N0 2m N0 2 л / |
(3.12) |
где N0 – начальное число электронов, |
m — число шагов развития лавины, – |
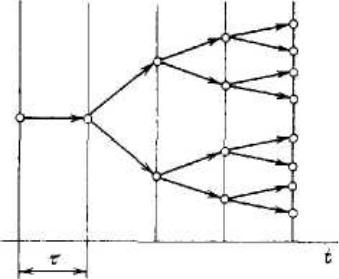
характерное время, необходимое для ускорения электрона до кинетической энергии n ведущей к ионизации, л – длительность лазерного импульса. Из (3.12) следует, что число электронов в лавине слабо зависит от числа "затравочных" электронов N0 , так как основное число свободных электронов образуется на последних шагах лавины (рис.3.1).
126
Рис. 3.1. Схема лавинного размножения электронов во времени
 52
52
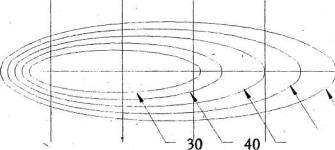
Рис. 3.2. Схема эволюции фронта плазмы в оптическом пробое в воздухе.
Цифры на кривых — время от начала пробоя в нс.
Область, охваченная ионизацией, расширяется навстречу излучению (рис.3.2). Расширение плазмы обусловлено гидродинамическим механизмом: нагреваемый газ, давление в котором велико, порождает ударную волну. Распространяясь навстречу лазерному пучку, ударная волна также ионизирует вещество, облегчая условия оптического пробоя. Новые порции вещества, ионизированные и прогретые ударной волной, становятся непрозрачными для излучения, которое сильно поглощается, и таким образом, поддерживает движение волны. Расширение может определяться также радиационным механизмом, в основе которого лежит прогрев вещества тепловым излучением, испускаемым горячей плазмой из области максимальной фокусировки лазерного излучения.
Условия для пробоя могут возникнуть в течение лазерного импульса во многих точках по пути луча. Отметим, что объем фокусировки V0 определяется поперечным размером лазерного пучка 2r0 , начальной расходимостью пучка перед фокусировкой, а также фокусным расстоянием линзы f
V |
f 4 3 |
. |
(3.13) |
|
|||
0 |
2r0 |
|
|
|
|
||
Оптический пробой в случае малых значений объема фокусировки наступает при более высоких значениях интенсивности световых пучков, т.к. элек-
127
троны очень быстро выводятся из области ионизации и лавины электронов не образуется.
В заключение надо отметить, что проведенное выше описание процесса ускорения свободного электрона в процессе ряда последовательных столкновений с нейтральными атомами и ионами является упрощенным. При этом были опущены различные явления, которые необходимо принимать во внимание в различных частных случаях. Одно из этих явлений — прилипание электронов к нейтральным атомам и молекулам с образованием отрицательных ионов; явление прилипания необходимо учитывать в средах, содержащих электроотрицательные атомы (молекулы) — кислород, органические соединения, галогены. Другое явление — рекомбинация электронов с положительными ионами; рекомбинацию необходимо учитывать в тех случаях, когда на конечной стадии достигается высокая степень ионизации нейтральных атомов, то есть когда высока концентрация ионов. Наконец, надо иметь в виду потери (диффузию) электронов из области пространства, в котором локализовано сильное световое поле, то есть из области фокусировки излучения; диффузию необходимо учитывать при малых размерах области фокусировки (например, при фокусировке одномодового излучения короткофокусными линзами) и при малой плотности газа, когда длина свободного пробега электрона сравнима с размерами области фокусировки излучения.
3.1.2. Оптический пробой идеально чистых твердых тел
Переходя к анализу процесса разрушения прозрачных твердых тел, сначала рассмотрим процесс разрушения идеально чистых сред, а потом обратимся к средам с локальными примесями. Разрушение прозрачных твердых тел описываются различными физическими процессами для идеально чистых сред и для сред, в которых имеются посторонние включения или примеси.
Первое, что надо иметь в виду, – идеально чистые твердые прозрачные среды практически не существуют. В любом кристалле, стекле всегда имеются макроскопические локальные примеси, представляющие собой локальные области, имеющие иной показатель преломления и коэффициент поглощения, чем сама среда. Типичным примером являются непрозрачные примеси. Эти примеси, как правило, носят технологический характер, они обусловлены методикой изготовления кристалла или стекла. Это могут бытьь частички платины, из которой изготавливаются тигли, в которых варят стекло. При среднем (по объему) коэффициенте поглощения прозрачных кристаллов и стекол порядка 10-3—10-5 см-1 локальный коэффициент поглощения таких примесей может достигать значений порядка 102—103 см-1, т. е. превышать среднее значение на много порядков величины. Однако некоторые кристаллы удается выращивать в таких условиях, когда количество примесей минимально. В качестве примера можно привести кристаллы NaCl и КС1. Результаты экспериментов с такими, почти совершенно однородными средами, могут с достаточным основанием сопоставляться с теорией пробоя идеально чистых сред.
В случае идеально чистых материалов механизм разрушения во многом похож на механизм оптического пробоя, рассмотренный выше. Лазерное излу-

128
чение за счет многостадийных взаимосвязанных процессов генерирует свободные носители зарядов. На свободных носителях происходит дополнительное поглощение лазерного излучения, при этом в облучаемом объеме выделяется тепло, повышается температура и показатель преломления среды, происходит самофокусировка пучка и повышается интенсивность излучения, что приводит к ускорению перечисленных процессов.
Прежде чем обратиться к описанию пробоя, сопоставим типичные характеристики кристаллов и стекол с характеристиками газов. Будем при этом исходить из основных черт процесса пробоя, возникающего за счет развития электронной лавины. Кратко напомним, что процесс пробоя заключается в создании свободных электронов, в увеличении энергии свободных электронов при столкновениях с третьим телом (в данном случае с решеткой) до значения, при котором ускоренный электрон может вырвать связанный электрон из третьего тела (в данном случае из валентной зоны); в развитии электронной лавины, приводящей к образованию критической плотности электронов для излучения заданной частоты; в эффективном, поглощении энергии излучения электронами, быстром локальном нагреве среды, повышении давления и разрушении твердого тела.
В процессе возникновения пробоя, обусловленного развитием электронной лавины, определяющее значение имеют плотность свободных электронов в среде, энергия, которую свободный электрон должен набрать за счет столкновений, частота столкновений электрона с третьим телом и наличие (или отсутствие) потерь энергии за счет конкурирующих процессов. В первых трех пунктах условия в кристаллах и стеклах значительно более благоприятны для развития лавинного пробоя, чем в газах.
Действительно, концентрация электронов в зоне проводимости (определяемая «хвостом» максвелловского распределения электронов по энергиям в валентной зоне) на много порядков превышает концентрацию свободных электронов в газе. Энергия, которую необходимо набрать электрону в зоне проводимости, равна ширине запрещенной зоны, которая меньше потенциала ионизации свободного атома или молекулы. Наконец, время свободного пробега электрона в зове проводимости (время до столкновения с решеткой) гораздо меньше времени свободного пробега в газе. Таким образом, все эти условия более благоприятны для развития пробоя, чем в газе.
С другой стороны, потери энергии при столкновениях электрона с решеткой существеннее, чем в случае столкновений с атомами. В результате столкновений с решеткой энергия теряется электроном на образование фононов. В интересующей нас области энергий электронов (0,1 - 10 эВ) частота столкновений с решеткой является резко убывающей функцией энергии. Соответственно резко убывает с ростом энергии электронов и скорость увеличения их энергии в
процессе столкновений dE dt . В этой же области энергий потери энергии на
образование фононов практически не зависят от энергии электронов,
dE dt const . Суммарный эффект зависит от напряженности поля лазерного
излучения, так как dE dt E2 . Очевидно, что всегда можно найти столь вы-
129
сокую напряженность поля E , когда суммарный эффект за время действия л лазерного импульса
л
dE dt dE
dt dE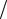 dt dt
dt dt
0
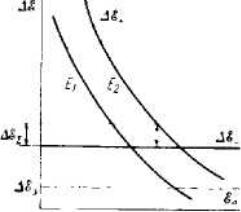
будет больше ширины запрещенной зоны Eз (рис. 3.3). Это и есть пороговое условие, необходимое для размножения свободных электронов.
Рис. 3.3. Изменении энергии электрона E в результате увеличения энергии электрона из-за антитормозного поглощения ( E ) и уменьшения энергии из-за возбуждения фононов ( E ) в зависимости от кинетической энергии электронов Ee
при различной напряженности поля E лазерного излучения; Ez — суммарный эффект изменения энергии электрона; Eз — ширина запрещенной зоны
Строгое количественное описание этого процесса проводится путем решения квантового кинетического уравнения для электронов, позволяющего получить зависимость напряженности поля, при которой возникает пробой, от параметров, характеризующих излучение ( , л ) и среду. Сопоставление результатов расчетов с экспериментальными данными, полученными для особо чистых кристаллов (NaCI, KC1) и лазерного излучения с энергией кванта примерно от 0,1 до 2 эВ, показало хорошее согласие для средних значений частот (1,2 эВ; 1,7 эВ) (рис. 3.4). Данные расчета и эксперимента для больших (2,36 эВ) и меньших (0,1—0,3 эВ) частот существенно различались. Было выяснено, что при малых частотах излучения развитие лавины сдерживалось недостатком начальных электронов, так как их образование за счет фотоионизации примесей или многофотонной ионизации атомов решетки при таких частотах происходит с меньшей эффективностью, чем при больших частотах. Этот вывод следовал из экспериментов с подсветкой кристалла ультрафиолетовым излучением, увеличивающим фотопроводимость. Наличие ультрафиолетового излучения понижало порог пробоя при основном длинноволновом излучении в несколько раз и не влияло на порог при основном коротковолновом излучении. В тех случаях, когда определяющим является образование начальных электронов в зоне проводимости, возникает зависимость порога пробоя от размера облучаемого объекта. В случае большой частоты излучения (2,30 эВ) следует предполагать,

130
что пробой обусловлен не возникновением электронной лавины, а процессом двухфотонной ионизации, который эффективно конкурирует с развитием лавины.
Рис. 3.4. Зависимость пороговой мощности q разрушения кристалла NaCI от его температуры при различных энергиях кванта лазерного излучения
3.1.2.1. Туннельное поглощение; переход Мотта диэлектрик-металл.
Ионизация квантовой системы может возникать и под действием постоянного внешнего электрического поля. В этом случае ионизация обусловлена возникновением потенциального барьера для электрона, связанного в атоме (рис. 3.5). При возникновении такого потенциального барьера к переходу связанного электрона в свободное состояние приводят два различных эффекта — надбарьерный распад связанной системы и туннельный эффект.
Рис. 3.5. Схема образования потенцнального барьера в постоянном внешнем
поле Econst ; u(r) – потенциал квантовой системы в отсутствие внешнего поля.
Если действие внешнего поля приводит к тому, что вершина барьера оказывается ниже энергии связи электрона, то связанная система перестает быть связанной – это процесс надбарьерного распада связанной системы.
