Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный университет Львовская политехника

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

matanaliz

.pdf

Скачиваний:

Добавлен:

12.02.2016

Размер:

1.22 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1312 13 > Следующая >>>

111

16.6. Замiна змiнно¨ та iнтегрування частинами у визначених iнтегра-

ëàõ

Теорема 16.4. Нехай функцiя f неперервна на [a; b], ' неперервна i ма¹ неперервну похiдну на [®; ¯], '(®) = a, '(¯) = b. Òîäi

Zb Z¯

f(x) dx = f('(t)) ¢ '0(t) dt:

a ®

Приклад.

0 = 0;

cos3 x dx =

sin2 x cos x dx =

t = sin x;

t1 = sin

dt = cos t dt;

t2 = sin

= 1

1 ¡ t2

dt = µt ¡ t3 ¶¯0 = 1 ¡ 3 ¡ (0 ¡ 0) = 3 :

Теорема 16.5. Нехай функцi¨

òà

неперервнi на

i мають неперервнi

[a; b]

ïîõiäíi. Òîäi

Zb u(x)v0(x) dx = u(x)v(x) ab

¡ Zb v(x)u0(x) dx

Приклад.

ln x dx

=	2	u = ln x	du = dxx

	4	dv = dx	v = x

5 = x ln xje1 ¡ dx = e ¡ e + 1 = 1:

112

ÐÎÇÄIË 17

ЗАСТОСУВАННЯ IНТЕГРАЛIВ

17.1. Обчислення площ

6y = f(x)

1. Нехай область G обмежена графiком функцi¨ y = f(x), x 2 [a; b], причому

f(x) ¸ 0, та прямими y = 0, x = a, x = b. Тодi площа цi¹¨ областi обчислю¹ться за

формулою: Z b

SG = f(x) dx: (17.1.1)

Зокрема, якщо крива, що обмежу¹ область G, задана параметрично

x = x(t); y = y(t); t 2 [®; ¯]; x(®) = a; x(¯) = b;

òî ìà¹ìî	b f(x) dx =	2
SG =			x = x(t);
	Za	4	dx = x0(t) dt

3	=	Z®	Z®
3	=	¯ f(x(t))x0(t) dt =	¯ y(t)x0(t) dt:
5

Отриму¹мо формулу:	Z®¯ y(t)x0(t) dt:
SG =	Z®¯ y(t)x0(t) dt:					(17.1.2)
Приклад. Обчислимо площу елiпса		x2	+	y2	= 1. З мiркувань симетрi¨ достатньо
Приклад. Обчислимо площу елiпса		2	+	2	= 1. З мiркувань симетрi¨ достатньо
		a		b

обчислити площу четвертинки елiпса i помножити ¨¨ на 4. В параметричнiй формi елiпс зада¹ться так: x = a cos t, y = b sin t, t 2 [0; 2¼].

	0				¼			¼
	0				2 sin2 t dt = 2ab			2 (1
S = 4		b sin t (	a sin t)dt = 4ab		2 sin2 t dt = 2ab			2 (1	cos 2t)dt =
Z	¼	¢ ¡			Z0			Z0	¡
Z	2	¢ ¡			Z0			Z0	¡
						¼
			= 2ab(t ¡	1		2	= ¼ab:
			= 2ab(t ¡	2 sin 2t)¯0			= ¼ab:
					¯
					¯
					¯

113

2. Нехай область G обмежена графiками двох функцiй y = f(x) òà y = g(x), x 2 [a; b], причому f(x) ¸ g(x), та прямими x = a i x = b. Тодi площа цi¹¨ областi обчислю¹ться за формулою:

					SG = Zab (f(x) ¡ g(x)) dx:	(17.1.3)
			-
			-		r = f(')
	--		-		©©©©
-	--			©©	©©©©
-			©©	©©
-		©	©©
¯		©
- ©
©					-
©- ®					-

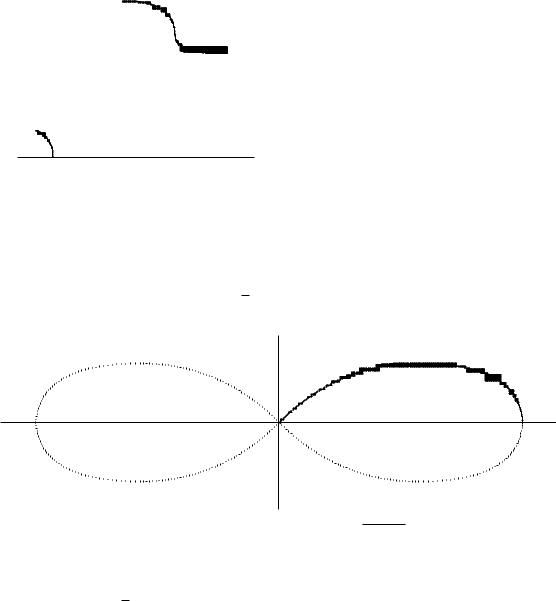
3. Нехай крива r = f('), ® · ' · ¯, задана у полярнiй системi координат. Площа сектора D, обмеженого променями ' = ® òà ' = ¯ i кривою r = f(') обчислю¹ться за формулою

				1		¯
				1	Z®		(f('))2 d':	(17.1.4)
				SD = 2	Z®		(f('))2 d':	(17.1.4)
				@			¡
				@			¡
				@			¡
				@			¡
					@¡			a-
					¡@
				¡			@
				¡			@
				¡			@
				¡			@
Приклад. Обчислимо площу лемнiскати r = apcos 2'.
	1	Z0	¼		Z0	¼
			4			4	¼
S = 4 ¢			4	r2 d' = 2a2		4	cos 2' d' = a2 sin 2'j04	= a2:
S = 4 ¢	2			r2 d' = 2a2			cos 2' d' = a2 sin 2'j04	= a2:

17.2.Обчислення довжини дуги криво¨

17.2.1.Довжина дуги криво¨ в прямокутних координатах.

114

¢yi

¢xi

Нехай крива l задана рiвнянням y = f(x), äå x 2 [a; b]. Нехай

x0 = a; x1; : : : ; xn = b

розбиття сегмента [a; b]. Позначимо 4xi = xi ¡ xi¡1, 4yi = f(xi) ¡ f(xi¡1). Позна- чимо Mi = (xi; f(xi)), i = 1; 2; : : : ; n точки криво¨ l. З'¹днавши цi точки послiдовно, ми отрима¹мо ламану M1M2 : : : Mn , вписану в криву l. Âiäðiçîê Mi¡1Mi назива¹ться

ланкою ламано¨. 4si

4si = p(4xi)2 + (4yi)2 = s1 + µ4yi ¶24xi:

4xi

Означення 17.1. Якщо iсну¹ границя довжин всiх ламаних, вписаних в криву l,

при умовi, що максимальна довжина ланок пряму¹ до нуля, то ця границя назива¹ться

довжиною криво¨ l. Крива l назива¹ться кривою скiнченно¨ довжини.

Теорема 17.1. Нехай функцiя f : [a; b] ! R неперервна разом зi сво¹ю першою похiдною. Тодi крива l = f(x; y) j y = f(x); x 2 [a; b]g ма¹ скiнченну довжину, яка обчислю¹ться за формулою

s = Zab q

dx:

1 + (f0(x))2

(17.2.1)

Приклад. Знайти довжину дуги параболи y = x2, x 2 [0; 1].

s = Z0

q1 + (2x)2dx =

4 ³2xp1 + 4x2 + ln ¯2x + p1 + 4x2¯´¯0 =

= p5 + 1 ln(2 + p5): 2 4

a2(1 + cos ')2 + a2 sin2 'd' = 2a

115

17.2.2. Довжина дуги криво¨, задано¨ параметрично. Нехай

x = x(t); y = y(t); t 2 [®; ¯]

параметрично задана крива. Припустимо, що x(t), y(t) неперервнi функцi¨, якi мають неперервнi першi похiднi. Тодi довжина криво¨ обчислю¹ться за формулою

s = Z®¯ q

dt:

(x0(t))2 + (y0(t))2

(17.2.2)

Приклад. Знайти довжину дуги криво¨ x = et cos t, y = et sin t âiä t = 0 äî t = 1.

s = Z0

1 p

dt =

(et cos t ¡ et sin t)2 + (et sin t + et cos t)2

= Z01 etp

dt = p

etj01 = p

2(e ¡ 1):

Нехай

x = x(t); y = y(t); z = z(t) t 2 [®; ¯]

просторова параметрично задана крива. Припустимо, що x(t), y(t), z(t) неперервнi

функцi¨, якi мають неперервнi першi похiднi. Тодi довжина криво¨ обчислю¹ться за формулою

	s = Z®¯ q				dt:
			(x0(t))2 + (y0(t))2 + (z0(t))2			(17.2.3)
Приклад. Знайти довжину гвинтово¨ лiнi¨
x = a cos t; y = a sin t; z = amt ïðè				t 2 [0; 2¼]:
s = Z02¼	p	a2 sin2 t + a2 cos2 t + a2m2dt = a		1 + m2		¢ 2¼:
				p

17.2.3. Довжина дуги криво¨ в полярнiй системi координат. Нехай в полярнiй системi координат крива задана рiвнянням r = r('), ' 2 ['1; '2]. Тодi довжина

дуги криво¨ обчислю¹ться за формулою:

Z '2 p

s =

r2(') + (r0('))2d':

(17.2.4)

Приклад. Знайти довжину кардiо¨ди

Z ¼ q

s = 2

r = a(1 + cos ').

Z ¼ p

2 + 2 cos 'd' =

0 0

= 4a Z0

d' = 4a Z0

cos 2 d' = 8a sin 2

= 8a:

1 + cos '

' ¼

116

17.3. Обчислення об'¹мiв тiл за площами поперечних перерiзiв

Нехай ма¹мо тiло T , проекцi¹ю якого на вiсь Ox ¹ âiäðiçîê [a; b]. Позначимо через

Q(x0) площу перерiзу тiла T площиною x = x0, x0 2 [a; b]. Òîäi

V = Zab

Q(x) dx:

(17.3.1)

Приклад. Знайдемо об'¹м елiпсо¨да

= 1:

Çàôiêñó¹ìî x0 = [2¡a; a] i розглянемо перерiз x = x0. Це елiпс, його площа дорiв-

íþ¹ S(x0) = ¼bc ³1 ¡

´. Òîìó îá'¹ì åëiïñî¨äà äîðiâíþ¹

= 3 ¼abc:

V = 2 Z0

¼bc µ1 ¡ a2

¶dx =

µa2x ¡

¶¯¯0

2¼bc

17.4. Об'¹м тiла обертання

Нехай тiло T утворене обертанням графiка неперервно¨ невiд'¹мно¨ функцi¨ f : [a; b] ! R навколо осi Ox. Очевидно, що Q(x) = ¼f2(x). Òîìó îá'¹ì òiëà îá÷è-

слю¹ться за формулою:

V = ¼ Zab f2(x)dx:

(17.4.1)

Площа боково¨ поверхнi обчислю¹ться за формулою:

P = 2¼ Zab f(x)q

dx:

1 + (f0(x))2

(17.4.2)

Приклад. Нехай тiло

T утворене обертанням y = cos x, x 2 £¡

;

¤ навколо осi

Ox. Знайдемо його об'¹м:

cos2 x dx = ¼ Z0

µx +

(1 + cos 2x) dx = ¼

;

V = 2¼ Z0

2 sin 2x¶¯¯0

P = 2 ¢ 2¼ Z0 2 cos x

1 + sin2 xdx =

¯0

sin x

1 + sin2 x + ln j sin x + 1 + sin2 xj

= 2¼

p2 + ln(1 + p2) :

= 4¼ 2

117

ÐÎÇÄIË 18

НЕВЛАСНI IНТЕГРАЛИ ТА IНТЕГРАЛИ, ЗАЛЕЖНI ВIД ПАРАМЕТРА

1.Iнтеграли по безмежному промiжку

2.Властивостi невласних iнтегралiв

3.Iнтеграли вiд необмежено¨ функцi¨

4.Iнтеграли, залежнi вiд параметра

18.1. Iнтеграли по безмежному промiжку

Нехай f : [a; +1) ! R неперервна функцiя.

Означення 18.1. Якщо iсну¹ скiнченна границя

lim f(x) dx;

b!+1

то вона назива¹ться невласним iнтегралом вiд функцi¨ f ïî ïðîìiæêó [a; +1) i познача¹ться

Za	f(x) dx =	b!+1 Za
+1		b
	def	lim f(x) dx:

При цьому говорять, що невласний iнтеграл çáiãà¹òüñÿ ÷è iñíó¹. Якщо ж границя

lim f(x) dx не iсну¹ чи безмежна, то кажуть, що невласний iнтеграл íå iñíó¹ ÷è

b +

! 1 R

ðîçáiãà¹òüñÿ.

Геометричний змiст невласного iнтеграла площа вiдповiдно¨ безмежно¨ обла-

стi. Якщо площа скiнченна iнтеграл збiга¹ться i навпаки.

Приклад 1.

lim

(arctg b

arctg 0) = ¼

1+x2

b +

! 1bR

! 1

Приклад 2.

= b

lim

lim (ln

1 + b

j ¡

ln 1) = +

1+x

! 1 R

! 1

Даний iнтеграл розбiжний.

118

Приклад 3.

x®

x® = b +

´¯

;

ïðè ® = 1;

® b®¡11

dx =

lim

(1¡®)x

1 ;

ïðè ® > 1;

®1

1 ;

ïðè ® > 1;

! 1

(ln x )

;

ïðè ® = 1

b +

ïðè

lim

® > 1

+1;

® · 1:

! 1

ln b;

ïðè ® = 1

! 1

Îòæå, ïðè

+1 dx

çáiæíèé, à ïðè

ðîçáiæíèé.

Аналогiчно визнача¹мо

def

lim

f(x) dx;

f(x) dx =

a!¡1 Z

¡1

f(x) dx def= Z

f(x) dx +

f(x) dx:

¡1

Остання рiвнiсть означа¹, що iнтеграл злiва збiга¹ться, якщо збiгаються два iнтеграли справа.

18.2. Властивостi невласних iнтегралiв

Теорема 18.1. Нехай f; g : [a; +1) ! R двi функцi¨ такi, що 0 · f(x) · g(x)

для всякого x 2 [a; +1). Òîäi

(à) ÿêùî

g(x) dx çáiæíèé, òî i

f(x) dx çáiæíèé;

(á) ÿêùî

f(x) dx ðîçáiæíèé, òî ðîçáiæíèé i

g(x) dx.

Приклад 4. Встановити, чи збiга¹ться iнтеграл

(1+ex)

1 dx

Îñêiëüêè 0 ·

, à

збiга¹ться, то збiга¹ться i наш iнтеграл.

x2(1+ex)

+1 x+1

Приклад 5. Встановити, чи збiга¹ться iнтеграл

dx.

iнтеграл.

x+1

Îñêiëüêè 0 < p

, à

dx ðîçáiãà¹òüñÿ, òî ðîçáiæíèé i íàø

Теорема 18.2. Якщо збiга¹ться iнтеграл

jf(x)j dx, то збiга¹ться також

iнтеграл

f(x) dx.

В цьому випадку iнтеграл +R1f(x) dx називають абсолютно збiжним.

119

Îñêiëüêè				+1			R
Приклад 6. Встановити, чи збiга¹ться iнтеграл							+1	sin x	dx.
Приклад 6. Встановити, чи збiга¹ться iнтеграл							a	x2	dx.
çáiæíèé.				R			a
çáiæíèé.	j sin xj		1	R	1	збiжний, то наш iнтеграл абсолютно
	j sin xj	· x2 , а iнтеграл		a x2 dx		збiжний, то наш iнтеграл абсолютно
	x2	· x2 , а iнтеграл		a x2 dx

18.3. Iнтеграли вiд необмежених функцiй

Нехай f : [a; b) ! R неперервна функцiя, а в точцi b вона або невизначена, або ма¹ розрив.

Означення 18.2. Якщо iсну¹ границя

Zc Zb

lim	f(x) dx def= f(x) dx;

c!d¡0

то вона назива¹ться невласним iнтегралом функцi¨ f ïî ïðîìiæêó [a; b).

f : (a;¯ b]

ÿêà¡

â òî÷öi a

Приклад 7. 1

lim 2p

2 = 2.

= lim

lim

1 b

1¡x

b!1¡0 0 1¡x

¡ b!1¡0

! R

¡ ¡

¡ b!1¡0

Аналогiчно визнача¹ться iнтеграл вiд функцi¨

àáî

невизначена, або ма¹ розрив.

18.4. Iнтеграли, залежнi вiд параметра

Розглянемо iнтеграл

I(®) = f(x; ®) dx;

який залежить вiд параметра ®. Нехай неперервна функцiя двох змiнних f визначена в областi f(x; y) 2 R2 j a · x · b; c · ® · dg i ма¹ неперервну похiдну по ®. Òîäi

I0(®) = f®0 (x; ®) dx:

(18.4.1)

Ця формула назива¹ться фомулою Лейбнiца. Нехай межi iнтегрування теж залежать вiд ®:

bZ(®)

I(®) =

f(x; ®) dx:

a(®)

								120
Òîäi	b(®)
	b(®)
I0(®) =	Z	f®0	(x; ®) dx + f (b(®); ®)	db	¡ f (a(®); ®)	da	:	(18.4.2)

				d®		d®
	a(®)
Приклад 8. Гама-функцiя
Розглянемо iнтеграл, який залежить вiд параметра ®
			+1
			Z
			x®¡1e¡x dx:					(18.4.3)
			0

Покажемо, що цей невласний iнтеграл iсну¹ при ® > 0. Зобразимо його у виглядi суми

+1	1	+1
Z0	x®¡1e¡x dx = Z0	x®¡1e¡x dx + Z1	x®¡1e¡x dx:

Перший iнтеграл збiга¹ться, так як

1	1
0 < Z	x®¡1e¡x dx < Z	x®¡1 dx =	1	:

			®

Другий iнтеграл теж збiжний. Нехай n 2 Z òàêå, ùî n > ® ¡ 1. Òîäi

+1		+1
0 < Z1	x®¡1e¡x dx <	Z1	xne¡x dx < +1:

Щоб обчислити останнiй iнтеграл, потрiбно взяти його n раз частинами i врахувати,

ùî lim xxn	= 0. Тобто ми означили деяку функцiю
x!1 e		Z0	xex dx:
	¡(®) =	Z0	xex dx:	(18.4.4)
		+1	®¡1

яку називають гама-функцi¹ю i часто використовують в застосуваннях математики.

+1	1			¡		¡x	¢¯¯	b
0	1			¡	¡e		¢¯¯	b
¡(1) =		dx =	lim						= 1:
Z	ex		b!+1					0

Нехай цiле число ® > 1.

¡(®) =

xex

dx =

2 dv = e¡x dx

®¡1

u = x®¡1

xex

¡x®¡1e¡x 0

+ (® ¡ 1)

®¡2

du = (® ¡ 1)x®¡2 dx 5 = v = ¡e¡x

dx = (® ¡ 1)¡(® ¡ 1):

Ми отримали рекурентну формулу

¡(®) = (® ¡ 1)¡(® ¡ 1):

(18.4.5)

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1312 13 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.02.20169.3 Mб15Marcotte_E._-_Responsive_Web_Design_(A_Book_Apart_Brief_books_for_people_who_make_websites)_-_2011.pdf
#
12.02.201667.97 Кб28marketing_lektsiyi.docx
#
01.05.2025107.01 Кб0marketing_testy_zaochnoe.doc
#
12.02.2016192.61 Кб105Mary_Poppins-Travers_P.L.rtf
#
01.05.20252.16 Mб0matan2modylli.teor.2.doc
#
12.02.20161.22 Mб19matanaliz.pdf
#
12.02.2016516.28 Кб21MATAN_LECT.pdf
#
01.05.2025141.73 Кб0matbalans.docx
#
12.08.201953.32 Кб2Mater.vidpov. storin.docx
#
01.04.2025212.48 Кб0materialne_ta_procesualne_pravo.doc
#
12.02.20161.56 Mб312Material_dlya_zmistu_Praktikumu_z_psikh_kons_12shr.doc