Множини. Методичка

A U \ A

Закони теорії множин

Для роботи із множинами часто використовують закони, наведені у таблиці 4.1.

називається різниця об’єднання і перерізу даних множин та позначається

A B :

A B x | (x A B) (x A B) .

11

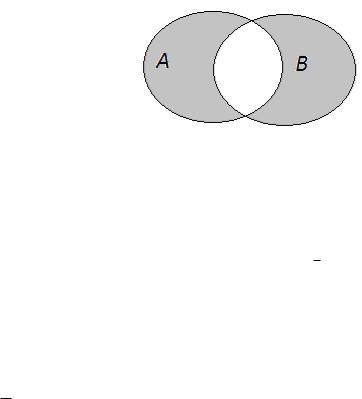
Геометрична ілюстрація:

через інші. Існує наступний пріоритет операцій: , , , \, . Для зміни цього

порядку у виразі використовують дужки.

Таким чином, множину можна задати виразом, в який входять множини, операції і можуть бути дужки. Такий спосіб задання множини називається аналітичним.

Приклад 4.5. Нехай U 1,2,3,4,5 ; A 1,3,4 ; B 2,3 ; C 1,4 . A B {1,3,4} 1,4 1,4 ;

A B 3 1,2,4,5 ;

B \ A C 2 C 1,2,4 .▲

Означення 4.6. Кортеж – це впорядкований набір елементів. Означення 4.7. Компоненти кортежу – елементи, що утворюють

кортеж.

На відміну від множини, компоненти кортежу можуть повторюватись. Кортеж записують у круглих дужках, наприклад, (a, b, c, a, d, k) – кортеж довжиною 6. Кортежі довжини два часто називають парами, а довжини 3 –

трійками.

Означення 4.8. Два кортежі називаються рівними, якщо вони мають однакову довжину та їхні відповідні компоненти рівні. Тобто, кортежі

12

n

пишуть A A A ... A і кажуть про n-й декартовий степінь множини A.

n разів

Елементами An є послідовності (набори, вектори, рядки) ( a1,a2 ,...,an )

довжиною n.

Приклад 4.6.

1.Нехай A 0,1 , B {x, y},C {0,1,2}. Тоді A B {(0, x),(0, y),(1, x),(1, y)};

B A {(x,0),( y,0),(x,1),( y,1)};

A C {(0,0),(1,2),(0,2),(1,0),(1,1),(1,2)}; A C {(0,0),(1,2),(0,2),(1,0),(1,1),(1,2)}.

2.Нехай A a,b,c,d,e, f , g,h , B {1,2,3,4,5,6,7,8} – множини символів,

які позначають горизонтальні і вертикальні поля шахівниці. Тоді A B {a1,a2,...,h7,h8}– множина всіх кодів кліток шахівниці.▲

Для скінченних множин потужність (кількість елементів) декартового добутку дорівнює добутку потужностей цих множин:

A B A B.

виключення.

Приклад 5.1. Скільки чисел серед 1,2,3,…,99,100 таких, що не діляться на жодне з чисел 2,3,5?

Підрахуємо спочатку кількість чисел, які діляться принаймні на одне з

Тому, використавши формулу обчислення потужності для об’єднання

13

трьох множин, маємо:

A1 A2 A3 50 33 20 (16 10 6) 3 74.

Отже, кількість чисел, які не діляться на жодне з чисел 2,3,5, дорівнює

100-74=26. 

ТЕОРЕМА 5.1. Для довільних множин Ak, k=1..n виконується:

Приклад 5.2. Розглядаються всі перестановки n чисел 1,2,…,n. Знайти число Dn тих перестановок, у яких принаймні одне число стоїть на місці зі своїм номером.

Позначимо через Ak множину тих перестановок, у яких на k-му місці стоїть k. Тоді

Принцип включення-виключення в альтернативній формі

Ця форма принципу включення-виключення використовується для розв’язування задач, де необхідно знайти кількість елементів заданої

множини А, які не мають жодної з n властивостей 1, 2 ,..., n. Позначимо:

Ai A – підмножина елементів, що мають властивість i ;

N(i1 , i2 ,..., in ) – кількість елементів множини А, які одночасно мають властивості i1 , i2 ,..., in ;

N (1, 2 ,..., n ) – кількість елементів множини А, що не мають жодної властивості i1 , i2 ,..., in ;

N – кількість елементів множини А.

14

Тоді

N(1, 2 ,..., n ) N | A1 A2 ... An | .

За принципом включення-виключення отримаємо:

N (i , a j , ak ) ... ( 1)n N (1, a2 ,..., an ).

1 i j k n

6. Доведення рівностей з множинами

Доводити рівності з множинами можна різними способами.

Спосіб 1. Для доведення рівності використовується теорема про те, що дві множини А та В рівні тоді й лише тоді, коли A B та B A.

Приклад 6.1. Доведемо рівність множин, яка є формулюванням закону де Моргана A B B A .

Припустимо, що x A B . Тоді x A B , звідси x Aабо x B . Отже

x B . Це означає, що x A B , тобто x A B . Отже A B A B . Cпосіб 2. Доведення рівності множин із використанням таблиць

належності. У цих таблицях розглядають усі можливі комбінації належності елементів множинам і позначають 1, якщо елемент належить множині, 0 –

Стовпчики, які в табл. 6.1 відповідають множинам A B та A B збіглися, отже A B A B .

Спосіб 3. Доведення рівності множин з використанням законів логіки.

Приклад 6.3. Доведемо попередню рівність A B A B . Доведення полягає в послідовній перевірці наступних рівностей

A B x x A B x (x A B) 15

x ((x A) (x B)) x (x A) (x B)

x (x A) (x B) x x A B A B .

Спосіб 4. Доведення рівності множин із використанням основних законів (табл. 3.1).

7. Комп’ютерне представлення множин

Зобразити множини у комп’ютері можна різними способами. Наприклад, накопичити елементи множини в невпорядкованому вигляді. Але тоді операції із множинами вимагатимуть значних ресурсів часу, адже щоразу необхідно буде здійснювати перегляд елементів. Тому є інші способи зображення множин у комп'ютері.

Одним із найпоширеніших та найпростіших способів є зображення множин за допомогою бітових рядків. Нехай універсальна множина U містить п елементів. Упорядкуємо довільним способом елементи універсальної множини. Тоді U a1,a2 ,a3 ,...an 1,an .

Множину A U зображають у комп'ютері рядком із 0 та 1 довжини п так: якщо ai A , то і-й біт дорівнює 1, якщо ai A , то і-й біт дорівнює 0.

множину В – рядком 110001100100.  Після представлення множин у вигляді бітових рядків, легко робити

операції над ними, адже це будуть порозрядні логічні операції над відповідними рядками.

Наприклад, перетин множин – це порозрядна кон'юнкція над бітовими рядками, а об'єднання множин – порозрядна диз'юнкція над бітовими рядками.

Логічні операції наведені в табл. 7.1.

Таблиця 7.1.

16

B a,b, f ,m,q . Знайдемо об'єднання множин A B . Виконаємо порозрядну

диз'юнкцію рядків, які зображають множини А та В: A = 010000110110;

B = 110001100100;

A B = 110001110110.

Отже, A B {a,b, f ,m,n,q,r}.

Якщо універсальна множина U має велику потужність, а підмножини універсальної множини не дуже потужні, то зображення за допомогою бітових рядків не є ефективним з точки зору витрат пам'яті. У такому разі для зображення множин доцільно використовувати інші структури даних – як правило, зв'язані списки, масиви або хеш-таблиці.

17

8. Приклади розв’язування завдань

Приклад 8.1. Задати двома різними способами множину А всіх парних чисел 2, 4, 6, ...., що не перевищують 1000.

Розв’язання:

1.Перерахуванням: А={2, 4, 6, 8, 10, …, 998, 1000};

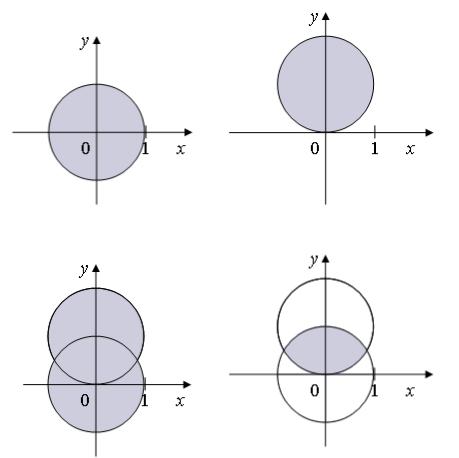
площина. Які фігури зображають множини A B, A B,R2 \ A ?

Розв’язання:

18

Множина R2 \ A

Приклад 8.3. Чи правильні рівності:

1){{1,2}, {2,3}}={1,2,3}?

2){{1,2}}={1,2}?

Розв’язання:

1)Ні, адже елементами першої множини є підмножини {1,2} та {2,3}, а другої – елементи 1,2,3.

2)Ні, тому що перша множина одноелементна, тобто складається з одного елемента – підмножини {1,2}, а друга має два елементи 1 та 2. ▲

Приклад 8.4. Перечисліть елементи наступних множин:

1)А={a|a B, B={1,2,3}};

2)A={a|a B, B={1,2,3}}.

Розв’язання:

1)Так, як а В, а В – трьохелементна множина, то існує 23=8

підмножин: А={{1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}, }. 2) Так, як а В, то А=В={1,2,3}.▲

Приклад 8.5. Довести, використовуючи закони алгебри множин, що

A (B \ A) A B.

Розв’язання:

A (B \ A) A (B A) ( A B) (A A) (A B) U A B. ▲

Приклад 8.6. Спростити вираз (A B C) (A B C) B C .

Розв’язання:

Використовуючи закони алгебри множин:

( A B C) ( A B C) B C [(A A) B C] B C ▲ U B C B C (B C) (B C) U

Приклад 8.7. Опитування 100 студентів показало, що серед них англійську мову вивчають 29 студентів, німецьку – 30, французьку – 9, лише французьку – 1, англійську та німецьку – 10, німецьку та французьку – 4, всі

19

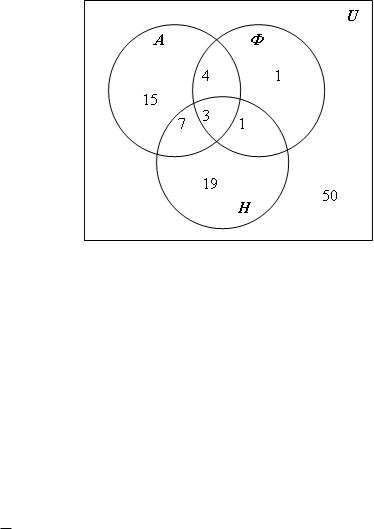
три мови – 3 студенти. Скільки студентів не вивчають жодної мови? Скільки студентів вивчають лише німецьку мову? У розв’язку використовувати діаграми Ейлера-Венна.

випадку лише німецьку мову вивчають 30-7-3-1=19 студентів.

Із умови задачі також випливає, що (А Ф) \ (А Ф Н ) 9-1-1-3=4,

тому лише англійську мову вивчають 29-4-3-7=15 студентів. Тоді число студентів, що не вивчають жодної мови, буде рівним U \ ( А Ф Н ) 100-

(1+1+3+4+7+15+19)=50 студентів.

Рис. 8.1 Діаграма Ейлера-Венна

Приклад 8.8. Довести, що для будь-яких множин А та В виконується

a (B B ) =, тобто отримали суперечність.

20