
LABORATORNIJ_PRAKTIKUM_Z_FIZIKI
.pdf
Розділ 3. Механічні коливання і хвилі
Інтерференція хвиль. Стоячі хвилі
Хвилі називаються когерентними, якщо вони мають однакову частоту і різниця їх фаз залишається постійною в часі:
ω1 = ω2 ;
φ = (φ1 – φ2).
Інтерференція – це явище перерозподілу енергії хвиль у просторі з утворенням стійких у часі областей максимуму і мінімуму енерґії, яке відбувається
в результаті накладання когерентних хвиль.
Особливим випадком інтерференції є утворення стоячих хвиль. Стоячі хвилі – це результат накладання двох біжучих
когерентних хвиль з однаковими амплітудами, які поширюються назустріч одна одній:
ω1 = ω2 ; |
φ = const ; A1 = A2 = A . |
ξ= A cos (ω t - k x) + A cos (ω t + k x) =
=A(cos ωt cos kx + sin ωt sin kx + cos ωt cos kx - sin ωt sin kx)
ξ = 2 A cos k x cos ω t . |
(3.52) |
||||||
Амплітуда стоячої хвилі залежить від координати x: |
|
||||||
Aст = |
|
2 A cos k x |
|
. |
(3.53) |
||
|
|
||||||
В точках середовища, де |
|
||||||
k x = ± m π (m = 0, 1, 2, …), |
(3.54) |
||||||
амплітуда Аст досягає максимального значення, яке дорівнює 2А. |
|||||||
Ці точки називаються пучностями стоячої хвилі. |
|
||||||
У точках середовища, де |
|
||||||
k x = ± (2 m + 1) |
π |
(m = 0, 1, 2, …), |
(3.55) |
||||
|
|||||||
2 |
|
|
|
|
|||
амплітуда Аст = 0.
Ці точки називаються вузлами стоячої хвилі.
31

Теоретична частина
З рівнянь (3.54) і (3.55) отримаємо координати пучностей та вузлів:
xп = ± m λ ; |
|
|
(3.56) |
|
2 |
|
|
|
|
xв = ± (2 m + 1) |
λ |
. |
(3.57) |
|
4 |
||||
|
|
|
||
Відстань між двома сусідніми вузлами (або пучностями) |
||||
стоячої хвилі називають довжиною стоячої хвилі λст : |
|
|||
λст = λ . |
|
|
(3.58) |
|
2 |
|
|
|
|
Всі точки стоячої хвилі між двома вузлами коливаються з різними амплітудами, але з однаковими фазами.
Стояча хвиля не переносить енерґію, тому що падаюча і відбита хвилі однакової амплітуди несуть однакову енерґію в протилежних напрямках.
Якщо середовище, від якого відбувається відбивання, менш густе, то в місці відбивання отримується пучність, якщо більш густе – вузол.
32
Розділ 4. ЕЛЕМЕНТИ ГІДРОДИНАМІКИ
4.1. Основні поняття гідродинаміки
Гідродинаміка вивчає рух нестисливих рідин і їх взаємодію з
твердими тілами. Основними поняттями гідродинаміки є: |
|
|
||||||
Течія − сукупність |
частинок |
рухомої |
рідини. |
|||||
Лінії течії – лінії, |
дотичні до |
яких у кожній точці |
||||||
збігааються |
за напрямом з векторами |
|||||||
швидкостей частинок рідини, а густина |
||||||||
проведення ліній течії (відношення числа |
||||||||
ліній |
|
N до величини перпендикулярної |
||||||
до них площі |
S, |
через |
яку вони |
|||||
проходять) пропорційна величині швид- |
||||||||
кості у даній точці. |
|
|
|
|
||||
Стаціонарна течія − течія, |
|
для |
якої |
форма |
і розміщення |
|||
ліній течії, а також |
значення |
швид- |
||||||
кості |
у |
кожній |
точці |
незмінне в |
||||
часі. |
У випадку стаціонарних течій лінії |
|||||||
течії збігаються з траєкторіями частинок |
||||||||
рухомої рідини. |
|
|
|
|
|
|||
Трубка течії − поверхня, |
утворена |
лініями |
течії, |
|||||
проведеними |
через усі |
точки малого |
||||||
замкненого контура. |
|
|
|
|
||||
Струмінь − частина |
рідини, |
обмежена |
трубкою |
|||||
течії. |
|
|
|
|
|
|
|
|
Ідеальна рідина – рідина, |
в |
якій |
повністю |
відсутнє |
||||
внутрішнє тертя. |
|
|
|
|
|
|||
33
Теоретична частина
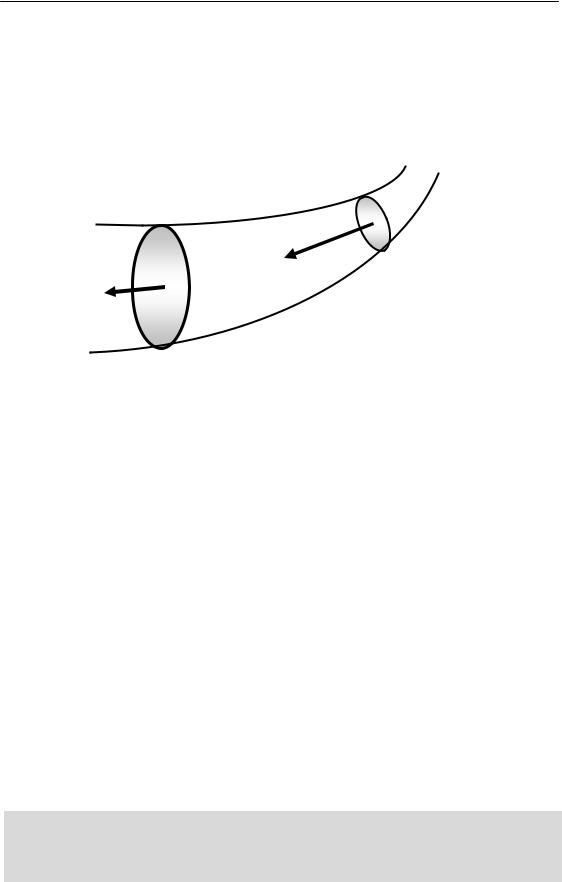
4.2. Рівняння нерозривності струменя (потоку)
Розглянемо ділянку елементарного струменя, обмеженого двома довільно вибраними нормальними перерізами, площі яких дорівнюють S1 та S2, а швидкості рідини відповідно – v1 та v2 .
S2
S2
v1
v2
Рис. 4.1
Якщо течія рідини стаціонарна, то маса рідини густиною ρ , що міститься між цими перерізами, не залежить від часу. Отже, маса рідини m = ρ v1S1 , яка надходить за одиницю часу в цей об’єм через перший переріз, повинна дорівнювати масі рідини m = ρ v2S2, яка витікає з виділеного об’єму за той самий час через
другий переріз : |
|
ρ v1S1 = ρ v2S2 . |
(4.1) |
У випадку нестисливої рідини (ρ = const) |
рівняння (1) |
набуває вигляду |
|
v1S1 = v2S2. |
(4.2) |
Оскільки перерізи S1 та S2 вибрані довільно, то |
|
vS = const. |
(4.3) |
Рівність (4.3) є виразом теореми про нерозривність струменя (потоку):
Маса рідини, що проходить за одиницю часу через кожний поперечний переріз трубки течії, для всіх перерізів однакова.
34
Розділ 4. Елементи гідродинаміки
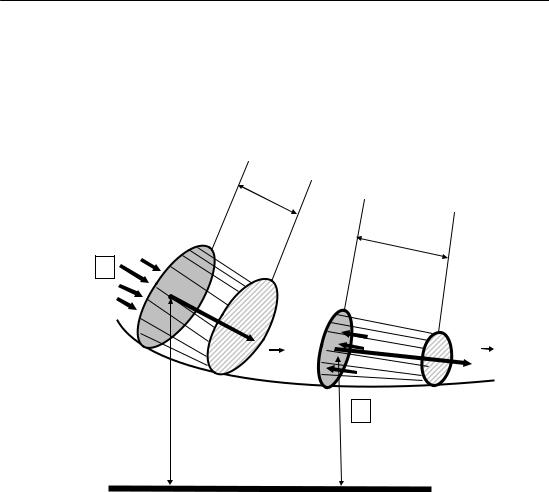
4.3. Рівняння Бернуллі
Стаціонарний рух ідеальної нестисливої рідини в полі сил тяжіння описує рівняння Бернуллі.
L1
S1 L2
p1 |
S1І |
S2
S2І
1 |
v2 |
h1 |
p2 |
|
h2 |
Рис. 4.2
Його отримують, застосувавши до руху рідини в тонкій трубці течії закон збереження енерґії. Нехай у місці перерізу S1 швидкість течії v1, тиск p1 і висота , на якій є цей переріз, h1 . Аналогічно у місці перерізу S2 швидкість течії v2, тиск p2 і висота перерізу h2. За малий проміжок часу t рідина переміщується від перерізів S1 і S2 до перерізів S1І і S2І.
Згідно з законом збереження механічної енерґії, зміна повної енерґії Е2 − Е1 ідеальної нестисливої рідини повинна дорівнювати
роботі А зовнішніх сил : |
|
Е2 − Е1 = А, |
(4.4) |
де Е1 і Е2 − повні енерґії рідини масою m у об’ємах, обмежених перерізами S1−S2 і S1І−S2І відповідно.
З іншого боку, А − це робота, яка виконується під час переміщення всієї рідини, розташованої між перерізами S1 і S2 за малий проміжок часу t. Для перенесення маси m від S1 до S1І рідина повинна переміститися на відстань L1 = v1 t і від S2 до S2І – на відстань L2 = v2 t . Зауважимо, що L1 і L2 настільки малі , що всі
35

Теоретична частина
точки виділених об’ємів мають сталі значення швидкості v, тиску p і висоти h. Отже,
A = F1L1 + F2L2, |
(4.5) |
де F1 і F2 сили тиску, що діють на рідину в місцях перерізів S1 і S2
|
|
|
F1 = p1S1 , |
|
(4.6) |
|||||||
|
|
|
F2 = – p2S2 . |
|
(4.7) |
|||||||
|
Сила F2 від’ємна, |
оскільки напрям її |
дії протилежний до |
|||||||||
напряму руху рідини. |
|
|
|
|
|
|
|
|
|
|||
|
Отже |
|
|
|
|
|
|
|
|
|
||
|
|
A = p1S1L1 – p2S2L2. |
|
(4.8) |
||||||||
|
Повні енерґії Е1 і Е2 складаються з кінетичної та потенціальної |
|||||||||||
енерґії маси m рідини: |
|
|
|
|
|
|
|
|
|
|||
|
|
|
E1 = |
1 |
mv12 +mgh1; |
|
(4.9) |
|||||
|
|
|
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
E2 = |
|
1 |
|
mv22 +mgh2. |
|
(4.10) |
|||
|
|
|
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
||||
|
Підставивши вирази (4.9), (4.10), (4.8) у формулу (4.4) та |
|||||||||||
врахувавши вирази для L1 і L2 , отримаємо |
|
|
||||||||||
|
1 |
mv12 +mgh1+p1S1v1 |
t = |
1 |
mv22 +mgh2+p2S2v2 |
t. (4.11) |
||||||
2 |
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
||||
|
Згідно з рівнянням нерозривності струменя (4.3) об’єм рідини |
|||||||||||
залишається сталим, тобто |
|
|
|
|
|
|
|
|
|
|||
|
|
V |
= S1v1 |
|
t = S2v2 |
t. |
(4.12) |
|||||
|
Розділивши вираз (4.11) |
на |
|
V і врахувавши, |
що перерізи |
|||||||
вибрані довільно, отримаємо рівняння Бернуллі |
|
|||||||||||
|
|
1ρv2 + ρgh + p = const, |
(4.13) |
|||||||||
2
де ρ − густина рідини.
Рівняння Бернуллі стверджує , що:
Для стаціонарної течії ідеальної нестисливої рідини сума динамічного 21ρv2 , гідростатичного ρgh і статичного p
тисків залишається сталою вздовж довільної лінії течії.
36

Розділ 4. Елементи гідродинаміки
Якщо трубка течії горизонтальна, то h = const і вираз (4.13) набуде вигляду:
1 |
ρv2 |
+ p = const, |
(4.14) |
|
2 |
||||
|
|
|
тобто тиск виявляється більшим у тих місцях, де швидкість течії менша. Отже, при протіканні рідини по трубі змінного перерізу згідно з (4.14) і рівнянням нерозривності струменя (4.3) тиск, а отже, і ймовірність розриву труби, вищі в місцях більшого діаметра труби.
37
Розділ 5. ТЕПЛОВЕ РОЗШИРЕННЯ ТВЕРДИХ ТІЛ
Тверді тіла при нагріванні розширюються. Це може призвести до виникнення значних механічних напруг, а тому в техніці доводиться запобігати наслідкам теплового розширення твердих тіл або враховувати їх.
Розширення твердого тіла при нагріванні пов’язане з характером теплового руху іонів і атомів, розміщених у вузлах кристалічної ґратки. Вказані частинки при Т>0 К коливаються навколо своїх положень рівноваги. Якщо припустити, що на певну частинку діє сила тільки з боку найближчих сусідніх частинок, а ті, своєю чергою, вважати умовно нерухомими, то ця сила лінійно залежить від величини зміщення x вибраної частинки з її положення рівноваги.
f = −kx , |
(5.1) |
де k – коефіцієнт пропорційності, величина якого залежить від природи твердого тіла.
Таку силу називають квазіпружною, а частинку, що коли-
вається під її дією, – гармонічним осцилятором. |
|
||
Потенціальна енерґія гармонічного осцилятора |
|
||
U = |
kx2 |
. |
(5.2) |
|
|||
2 |
|
|
|
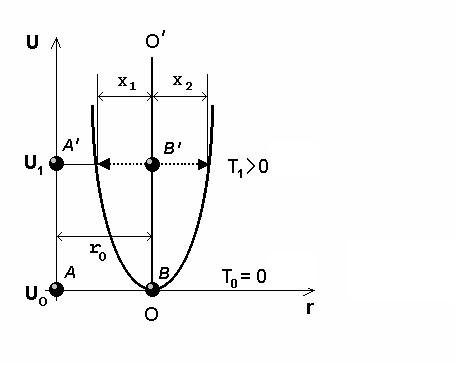
Розглянемо поведінку двох частинок твердого тіла A і B при T=0 K (Вони ж A′ і B′ при T>0 K). При T=0 К ці частинки нерухомі, відстань між ними дорівнює r0 , а потенціальна енерґія кожної з них
К
Рис. 5.1
К
38
Розділ 5. Теплове розширення твердих тіл
U0 . При T>0 K частинки починають коливатися навколо положень рівноваги; їх потенціальна енерґія U1 > U0 (рис. 5.1).
Для простоти вважатимемо, що коливання здійснює тільки частинка B′; тоді відстань r між частинками, зміщення частинки B′ від положення рівноваги x і r0 зв’язані рівнянням:
x = r − r0 |
|
|
= |
k(r − r |
)2 |
|
|
і |
U1 |
0 |
|
. |
(5.3) |
||
2 |
|
||||||
|
|
|
|
|
|
|
З огляду на симетрію кривої U(r) відносно прямої OO′, яка проходить через положення рівноваги частинки B при різних значеннях T, відхилення зазначеної частинки праворуч і ліворуч збігаються за величиною: x1 = x2 . Отже, нагрівання в такому
випадку не могло б викликати розширення тіла, тому що підвищення температури призводило б тільки до збільшення амплітуди коливань частинок, а середня відстань між ними залишалася б незмінною.
Насправді в реальних твердих тілах кожна частинка зазнає впливу як з боку сусідніх частинок, так і віддаленіших.
Тому залежність результуючої сили f , що діє на частинку, від зміщення частинки визначається співвідношенням:
f = −kx + γx2 ,
де k i γ визначається природою твердого тіла.
К
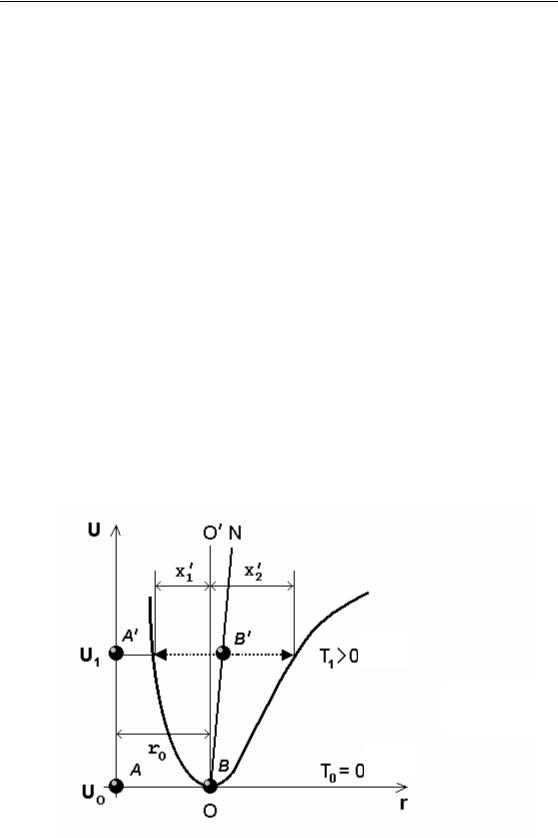
Рис. 5.2
К
Ця сила вже не є квазіпружною, а коливання частинки під її впливом не є гармонічним. Отже, у реальних твердих тілах частинки виступають як ангармонічні осцилятори.
Залежність U(r) для ангармонічного осцилятора зображена на рис. 5.2.
39

Теоретична частина
Несиметричний характер кривої ілюструє те, що при довільній T>0 K відхилення від положення рівноваги частинки B/ у
різних напрямах вздовж r виявляються неоднаковими.
Тому середнє положення такої частинки вже не збігатиметься з положенням рівноваги для гармонічного осцилятора. З підвищенням температури величина цього зміщення збільшується, середні положення частинки B/ для вищих температур будуть розташовані на прямій ON, а це означає збільшення середньої віддалі між частинками.
Отже, тверді тіла при нагріванні розширюються.
Ступінь розширення твердого тіла визначається коефіцієнтом лінійного теплового розширення.
Коефіцієнт лінійного теплового розширення α чисельно дорівнює відносній зміні лінійних розмірів тіла LL ,
зумовленій зміною його температури на 1 К.
α = |
L |
|
1 |
. |
(5.4) |
L |
|
||||
|
|
T |
|
||
Оскільки α = α(T) , формула (5.4) дає змогу визначити тільки |
|||||
середнє значення α для даного інтервалу |
T . |
||||
Коефіцієнт лінійного розширення при даній Т, визначений для безмежно малого інтервалу температури dT , називають істинним:
αi = |
dL |
|
1 |
. |
(5.5) |
|
|
||||
|
L dT |
|
|||
40
