Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный университет Львовская политехника

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

LABORATORNIJ_PRAKTIKUM_Z_FIZIKI

.pdf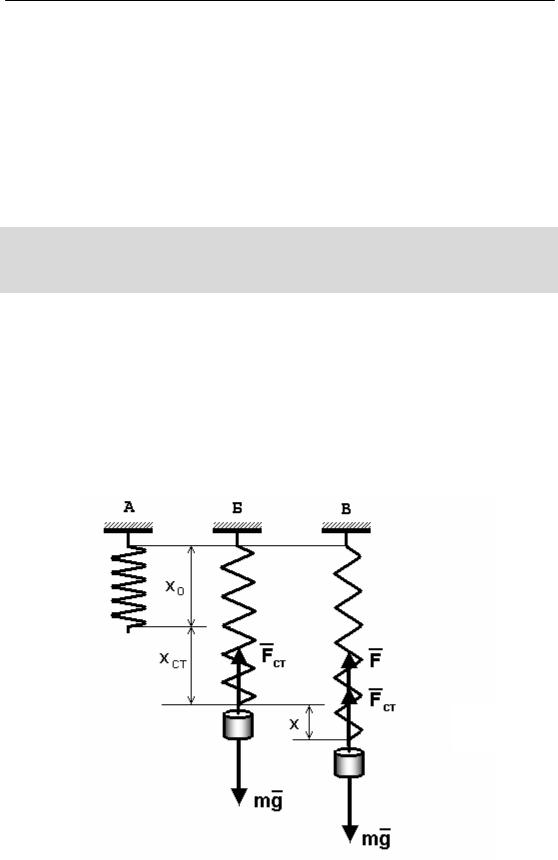

Скачиваний:

2278

Добавлен:

12.02.2016

Размер:

5.18 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 193 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 > Следующая >>>

Розділ 3. Механічні коливання і хвилі

Зв’язок між періодом і власною циклічною частотою коливань має вигляд:

ω0	=	2 π	.	(3.2)

		T

3.2. Пружинний маятник

Пружинний маятник – це тверде тіло, підвішене на абсолютно пружній невагомій пружині, яке під дією пружної сили може здійснювати гармонічні коливання.

Якщо тіло висить нерухомо (рис. 3.1Б), то пружина видовжена на xст (статичний розтяг) порівняно з ненавантаженою пружиною (рис. 3.1А), а умова рівноваги тіла запишеться у вигляді:

	m g - k xст = 0,	(3.3)
де – kxст =Fст	(k – коефіцієнт жорсткості пружини).

Рис. 3.1

Якщо тіло вивести з положення рівноваги (рис. 3.1В), то на нього буде діяти додатково сила пружності:

F = - k x

(3.4)

Теоретична частина

і другий закон Ньютона запишеться у вигляді: m g - k xст - k x = m α.

Врахувавши (3.3), рівняння (3.5) подамо у вигляді:

−	k x	=	&&	&& +	k	=	0

			m α=m x , або	x m x

mk > 0, тому можна представити

mk = ω20 .

З врахуванням (3.7) рівняння (3.6) набуде вигляду:

(3.5)

(3.6)

(3.7)

&& +	2	=		0 .		(3.8)
x	ω0 x
Розв’язок (3.8) є рівнянням гармонічних коливань:
x = A cos (ω0 t + φ0).						(3.9)
Період коливань визначається масою тіла і жорсткістю
пружини:

T = 2 π			m		.	(3.10)

			k

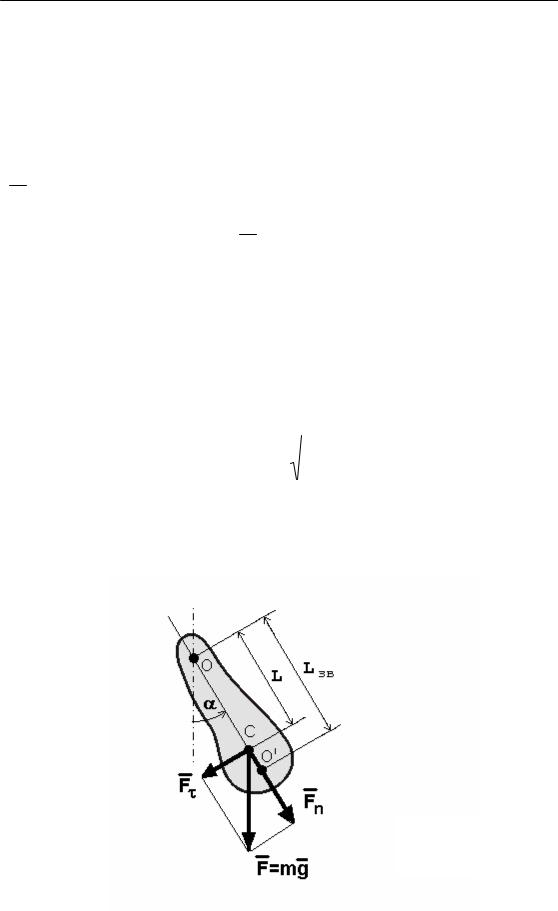
3.3. Фізичний маятник

Рис. 3.2

Розділ 3. Механічні коливання і хвилі

Фізичний маятник – це тверде тіло довільної форми, яке під дією сили тяжіння здійснює коливання навколо нерухомої горизонтальної осі, що не проходить

через центр маси тіла.

При відхиленні маятника від положення рівноваги на кут α

виникає обертальний момент (рис. 3.2):
M0 = Fτ L = - m g L sin α,	(3.11)

де Fτ = - m g sin α − складова сили тяжіння, яка повертає маятник у

положення рівноваги.

Використавши рівняння динаміки обертального руху твердого

тіла:

M0 = J0 ε,

(3.12)

де J0 – момент інерції маятника відносно осі, що проходить через точку О;

ε − кутове прискорення маятника

d2α

ε = dt2

(3.13)

одержимо:

α ,

(3.14)

J0 α = - m gL sin α ,

або

m g L

sin α = 0 .

α +

(3.15)

Позначивши:

m g L

ω02 =

(3.16)

одержуємо диференціальне рівняння коливань маятника:

sin α

(3.17)

ω0

Якщо кут відхилення α малий ( α < 60 ),

то sin α ≈ α ; рівняння

(3.17) набуде вигляду:

0 .

(3.18)

ω0 α

і його розв’язком є рівняння гармонічних коливань:

α = α0 cos (ω0 t + φ0),

(3.19)

де α0 – максимальний кут відхилення;

Теоретична частина

Період коливань фізичного маятника:

T = 2 π

Позначимо:

m g L

Lзв =

, тоді

T = 2 π

Lзв

m L

(3.20)

(3.21)

Зведена довжина фізичного маятника Lзв – це довжина такого математичного маятника,

період коливань якого збігається з періодом коливань даного фізичного маятника.

Оборотний маятник – це фізичний маятник, який має дві осі обертання, паралельні одна одній (О та О’ ). Ці осі знаходяться на віддалі Lзв. Точка О’називається центром гойдання. Точка підвісу О і центр гойдання О’ мають властивість взаємозамінності: при перенесенні точки підвісу у центр гойдання О’ попередня точка підвісу О стане новим центром гойдання. Період коливань при цьому не зміниться.

3.4. Математичний маятник

Математичний маятник – це підвішена на невагомій нерозтяжній нитці матеріальна точка, яка під дією сили

тяжіння може здійснювати періодичні коливання.

Математичний маятник можна розглядати як частинний випадок фізичного маятника, вся маса якого зосереджена в одній точці – центрі мас.

Період коливань такого маятника:

T = 2π

= 2π

mL2

(3.22)

mgL

де L – довжина нитки.

Таким чином, період коливань математичного маятника:

Т = 2π

(3.23)

Коливання математичного маятника, як і фізичного, є гармонічними лише при малих кутах відхилення.

Розділ 3. Механічні коливання і хвилі

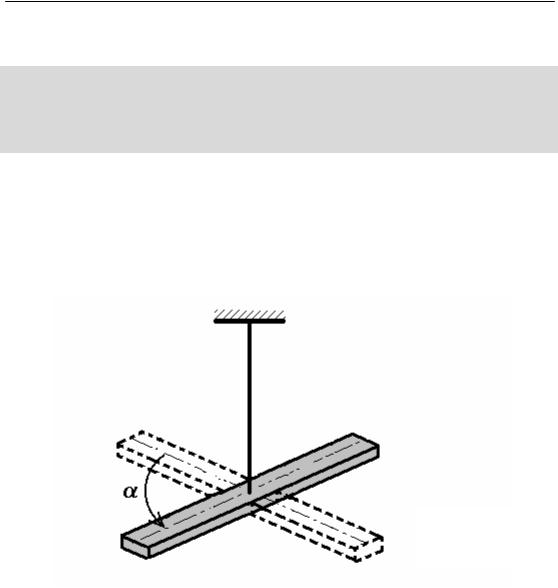
3.5. Крутильний маятник

Крутильний маятник – це тверде тіло, закріплене на жорсткій підвісці, яке може здійснювати крутильні

коливання під дією сил пружності деформації кручення підвіски.

При закручуванні маятника на кут α виникає момент пружної сили, який намагається повернути маятник у положення рівноваги

M = – fα ,

(3.24)

де f − модуль кручення дротини, який залежить від розмірів і пружних властивостей матеріалу дротини.

Рис. 3.3

Оскільки після закручування маятник буде здійснювати обертальний рух навколо своєї вертикальної осі, яка проходить через точку підвісу вздовж дротини, то:

M = Jε ,					(3.25)
де J – момент інерції маятника відносно осі закручування.
Врахувавши (3.13), (3.24), рівняння (3.25) запишемо у вигляді:
&&	+	f α	=	0,	(3.26)
J α		f α		0,	(3.26)
або
&&	+	f	= 0.
&&		J α			(3.27)
α		J α			(3.27)

Теоретична частина

Ввівши позначення :
ω02 =	f	,	(3.28)
	J

отримаємо диференціальне рівняння гармонічних коливань крутильного маятника:

&& +	2	α	=	0.			(3.29)
α	ω0	α		0.			(3.29)
Розв’язком (3.28) є рівняння гармонічних коливань:
α = α0 cos (ω0 t + φ0).							(3.30)
Період коливань крутильного маятника:

	T = 2 π				J	.	(3.31)
	T = 2 π					.	(3.31)
					f

3.6. Згасаючі коливання

Реальні механічні коливання здійснюються за наявності сил опору середовища. Тому механічна енерґія коливної системи з часом зменшується, а самі коливання згасають. Сила опору середовища переважно пропорційна швидкості руху тіла, що здійснює коливання:

Fоп = - r u ,

(3.32)

де r – коефіцієнт опору середовища, знак ( – ) вказує на протилежний напрям сили опору і швидкості руху.

Нехай тіло масою m під дією пружної сили −kx і сили опору

∙

− rux = −r x здійснює коливання

вздовж осі OX.

Рівняння руху

такого тіла:

k x

(3.33)

m x

r x

або

&& +

(3.34)

m x

Позначивши:

= ω02 ;

= 2 β ,

де β − коефіцієнт згасання,

Розділ 3. Механічні коливання і хвилі

запишемо диференціальне рівняння згасаючих коливань:

		&& +	& +	2	=	0.	(3.35)
		x	2 β x	ω0 x		0.	(3.35)
	Якщо	ω0 >β, розв’язком (3.35) є рівняння:
		x = A0e−βtcos(ωt + φ0),					(3.36)
яке	описує	гармонічні	коливання		з циклічною		частотою
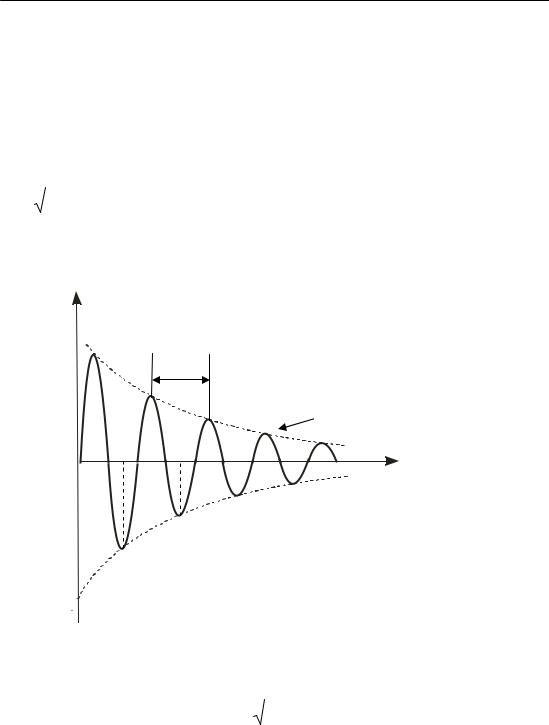
ω =		і змінною у часі амплітудою A = A0 e- β t
ω =	ω02 - β2	і змінною у часі амплітудою A = A0 e- β t					при почат-
ковій амплітуді А0 (рис. 3.4)

A = A0e−βt

		t
	An+1	Рис. 3.4
An	An+1	Рис. 3.4
An

Період згасаючих коливань:

T =	2 π	.	(3.37)

	ω02 - β2

∙Декрементом згасання D називається відношення амплітуд двох послідовних коливань:

D =	A	n	=	A	0	e- β t	= eβ T .	(3.38)
				A0 e- β(t + T)
	An+1

∙Лоґарифмічним декрементом згасання називається фізична величина:

λ = ln D = β T .

(3.39)

Теоретична частина

∙Часом релаксації коливальної системи τ називається проміжок часу, протягом якого амплітуда коливань зменшується в е разів (е – основа натурального лоґарифму). Коефіцієнтом згасання називається фізична величина, обернена до часу релаксації:

β =	1
β =	τ .	(3.40)

∙Nе – число коливань, після здійснення яких амплітуда зменшується в е разів, так що τ = NеT.

λ = βТ =	T	=	T	=		1	.	(3.41)
	τ		NeT
					Ne

Отже, лоґарифмічний декремент згасання − це фізична величина, обернена до числа коливань Ne, після здійснення яких амплітуда зменшується в е разів.

∙ Добротністю системи називається фізична величина:

Q = 2π	E	,	(3.42)
	E

де Е – енерґія системи у даний момент часу;

E – енерґія, втрачена протягом одного періоду.

Отже, добротність системи тим більша, чим менші втрати

енерґії системи E. Можна показати, що:
Q =	π	= π Ne .	(3.43)
	λ

3.7. Механічні хвилі

Хвиля – це процес поширення коливань у просторі. При поширенні хвилі частинки середовища не втягуються у поступальний рух, а лише коливаються навколо положень рівноваги. При цьому частинки обмінюються енерґією. Тому хвилі переносять енерґію без перенесення речовини.

Механічні (пружні) хвилі − це процес поширення коливань у пружному середовищі. Хвилі бувають поздовжніми і поперечними.

У випадку поперечної хвилі частинки середовища коливаються в напрямі, перпендикулярному до напряму поширення хвилі. Поперечні хвилі поширюються у середовищах, в яких виникають пружні сили при деформації зсуву, тобто в твердих тілах. Поперечна хвиля може поширюватися також на поверхні рідини.

Розділ 3. Механічні коливання і хвилі

Швидкість поширення поперечної хвилі:

u =	G	,	(3.44)
	ρ

де G – модуль зсуву,

ρ− густина середовища.

Увипадку поздовжньої хвилі частинки середовища коливаються у напрямі поширення хвилі. Поздовжні хвилі поширюються

усередовищах, де виникають пружні сили при деформаціях стиску (розтягу), тобто у твердих тілах, рідинах і газах. Швидкість поширення поздовжньої хвилі:

u =	E	,	(3.45)
	ρ

де Е – модуль Юнґа; ρ − густина середовища.

Для опису хвиль поряд з такими характеристиками, як амплітуда, період, частота, фаза використовують поняття:

∙хвильовий фронт – ґеометричне місце точок середовища, до яких доходять коливання в даний момент часу;

∙хвильова поверхня – ґеометричне місце точок, які коливаються в однаковій фазі. За формою хвильової поверхні розрізняють плоскі, сферичні й інші хвилі;

∙промінь –лінія, перпендикулярна до хвильової поверхні;

∙довжина хвилі ( λ ) – найменша відстань між двома точками середовища у напрямі, перпендикулярному до напряму поширення, які коливаються в однаковій фазі;

∙швидкість хвилі (u) – швидкість поширення постійної фази хвилі;

∙хвильове число − k = 2λπ .

Довжина хвилі, швидкість, період і частота ν зв’язані співвідношеннями:

λ = uT; u = λ ν.

Плоска біжуча хвиля

Хвилі, які переносять у просторі енерґію, називаються біжучими. Якщо плоска хвиля поширюється вздовж осі OX, то ξ –

Теоретична частина

зміщення з положення рівноваги частинок, що коливаються, залежить від їхніх координат x та часу t, тобто ξ = ξ(x, t) .

Частинка В знаходиться на відстані x від джерела коливань О (рис. 3.5). Якщо коливання частинок, які лежать в площині x=0, описуються функцією ξ(0, t) = A cos ω t, то частинка В коли-

ватиметься за таким самим законом, але її коливання запізню-

ватимуться у часі порівняно з коливаннями джерела на τ = ux

	x			u
		B		u
		B
0

					X
					X
						Рис. 3.5
			λ			Рис. 3.5
			λ

Тому рівняння біжучої хвилі має вигляд:
ξ(x, t) = A cos ω ( t -	x	) .	(3.46)

	u

Якщо плоска хвиля поширюється у протилежному напрямі, то:

ξ(x, t) = A cos ω( t +

(3.47)

У загальному випадку:

ξ(x, t) = A cos [ω(t −

) + φ0].

(3.48)

Враховуючи :

k =

2 π

u T

надамо рівнянню плоскої хвилі вигляду:

ξ(x, t) = A cos (ω t - k x + φ0).

(3.49)

<<< < Предыдущая 1 23 / 193 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.04.2025229.38 Кб0Laboratorna_robota__33_PERVINNI_ZASOBI_POZhEZhO...doc
#
01.04.20251.76 Mб0Laboratorna_robota__6_Vivchennya_umov_mikroklim...doc
#
22.11.2019177.15 Кб4Laboratorna_trubni_mlini.doc
#
15.08.201992.01 Кб5Laboratorna_z_el_tekhniki_2.docx
#
01.04.2025160.77 Кб0Laboratorni roboty_TZI_1_8.DOC
#
12.02.20165.18 Mб2278LABORATORNIJ_PRAKTIKUM_Z_FIZIKI.pdf
#
01.04.2025142.85 Кб0laboratorni_Элементы управления Windows Forms_.doc
#
02.05.2019215.04 Кб5Laboratory work №1.doc
#
21.11.2019113.15 Кб8Labor_2.doc
#
12.02.20161.61 Mб11Labor_2_KM.doc
#
12.02.20161.76 Mб16Labor_2_МОС_2012.doc