
LABORATORNIJ_PRAKTIKUM_Z_FIZIKI
.pdf
Лабораторна робота №8
Виведення розрахункової формули
Період коливань крутильного маятника визначається з формули:
T = 2π |
|
J |
, |
(1) |
|
f |
|||||
|
|
|
|
де J – момент інерції маятника.
Для визначення J за формулою (1), крім виміряного Т, необхідно знати модуль кручення дроту f. Це ускладнення можна обійти, навантажуючи крутильний маятник тілами правильної ґеометричної форми, момент інерції яких легко обчислити. У даній
роботі – це 8 металевих дисків, сумарна маса яких |
m . |
||||
Якщо диски насадити на шпильки α (по два диски на кожну |
|||||
шпильку), то період коливання одержаної системи |
|
||||
|
|
|
|
|
|
T = 2π |
J + J1 |
, |
(2) |
||
|
|||||
1 |
|
f |
|
||
|
|
|
|||
де J1 – сумарний момент інерції дисків відносно осі обертання маятника.
Якщо ж диски насадити на шпильки b (також по два на кожну шпильку), то період коливання системи
T = 2π |
J + J2 |
, |
(3) |
|
|||
2 |
f |
|
|
|
|
|
де J2 – сумарний момент інерції дисків відносно осі обертання маятника в новому положенні дисків.
З (2) і (3) у результаті нескладних перетворень одержимо:
J = |
J T2 |
− J T2 |
|
|
2 1 |
1 2 |
. |
(4) |
|
T2 |
|
|||
|
− T2 |
|
||
|
2 |
1 |
|
|
Для визначення J1 і J2 використаємо теорему Штайнера, |
||||
згідно з якою: |
|
|
|
|
J = J + md2 |
; |
J |
2 |
= J |
0 |
+ md2 |
, |
(5) |
||
1 |
0 |
1 |
|
|
|
2 |
|
|
||
де J0 – сумарний момент інерції всіх дисків відносно осі, що проходить через їх ґеометричний центр паралельно до осі обертання.
91
Інструкції до лабораторних робіт
Підставивши J1 i J2 з (5) в (4), одержимо: |
|
||||||||||||||||
J = |
m(T2d2 |
− T2d2 ) |
− J |
|
|
|
|||||||||||
|
1 |
|
2 |
2 |
1 |
|
|
0 |
. |
(6) |
|||||||
|
T2 |
− T2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Якщо сумарна маса дисків m, а діаметр диска D, то J0 |
|||||||||||||||||
визначиться як: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J0 |
= |
|
1 |
mD2 . |
|
|
|
|
|
|
|
|
|
|
(7) |
Отже |
|
8 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J = |
m(T2d2 |
− T2d2 ) |
− |
1 |
mD2 . |
|
|||||||||||
|
1 |
2 |
|
2 1 |
|
|
|
|
|
(8) |
|||||||
|
|
|
|
|
|
|
8 |
|
|||||||||
|
|
T2 |
− T2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
При підготовці до виконання роботи використати: Теоретична частина. Розділи 1.1, 1.2, 3.5.
Послідовність виконання роботи
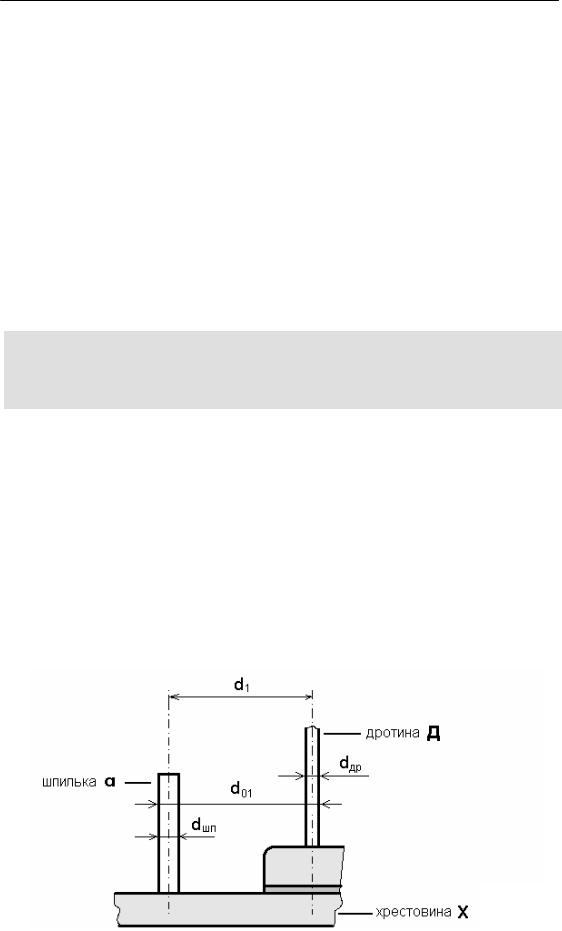
1. |
Вимірявши |
d01, |
dшп, dдр, |
(рис. |
2), |
знайти |
d1 і d1 за |
||||||
формулами: |
|
|
|
|
|
|
|
|
|
|
|
|
|
d1 |
= d01 |
− |
dдр |
− |
dшп |
; |
d1 |
= d01+ |
1 |
dдр+ |
1 |
dшп. |
|
2 |
2 |
|
2 |
2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
||||
Вимірювання провести по одному разу для кожної шпильки α.
Рис. 2
92

Лабораторна робота №8
2. Аналогічно визначити d2 і |
d2 для кожної шпильки b: |
||||||||||
d2 = d02 − |
dдр |
− |
dшп |
; |
d2 |
= d02+ |
1 |
dдр+ |
1 |
dшп. |
|
2 |
2 |
2 |
2 |
||||||||
|
|
|
|
|
|
|
|||||
(d02 – відстань між зовнішніми краями дротини Д і шпильки b).
3. Насадити диски на шпильки а (по два диски на кожну шпильку), привести систему в коливальний рух, закрутивши маятник на кут не більше 900 і виміряти час t1 десяти повних коливань. Визначити період Т1 за формулою:
T1 = 10t1 .
4. Переставивши диски на шпильки b, аналогічно визначити Т2. Вимірювання, зазначені в пунктах 3 і 4, провести по чотири
рази.
5.Виміряти діаметри D чотирьох довільно вибраних дисків.
6.Результати вимірювань записати в таблиці; за формулою (8) розрахувати J.
7.Визначити абсолютну і відносну похибки .
сумарна маса дисків m = (1,347 ± 0,006) кг.
GПри розрахунку J перевести результати вимірювань всіх величин в одиниці СІ.
Таблиці результатів вимірювань
№ |
dшп, |
dшп, |
dдр, |
dдр, |
d01, |
d01, |
d02, |
d02, |
|
мм |
мм |
мм |
мм |
мм |
мм |
мм |
мм |
||
|
|||||||||
1 |
вимір. |
розрах. |
вимір. |
розрах. |
вимір. |
розрах. |
вимір. |
розрах. |
|
2 |
вимір. |
розрах. |
вимір. |
розрах. |
вимір. |
розрах. |
вимір. |
розрах. |
|
3 |
вимір. |
розрах. |
вимір. |
розрах. |
вимір. |
розрах. |
вимір. |
розрах. |
|
4 |
вимір. |
розрах. |
вимір. |
розрах. |
вимір. |
розрах. |
вимір. |
розрах. |
|
сер. |
розрах. |
розрах. |
розрах. |
розрах. |
розрах. |
розрах. |
розрах. |
розрах. |
93

Інструкції до лабораторних робіт
№ |
d1, |
d1, |
d2, |
d2, |
T1, |
T1, |
Т2, |
ΔТ2, |
D, |
D, |
|
мм |
мм |
мм |
мм |
с |
c |
с |
с |
мм |
мм |
||
|
|||||||||||
1 |
|
|
|
|
розр. |
розр. |
розр. |
розр. |
вимір. |
розр. |
|
2 |
|
|
|
|
розр. |
розр. |
розр. |
розр. |
вимір. |
розр. |
|
3 |
|
|
|
|
розр. |
розр. |
розр. |
розр. |
вимір. |
розр. |
|
4 |
|
|
|
|
розр. |
розр. |
розр. |
розр. |
вимір. |
розр. |
|
сер. |
розр. |
розр. |
розр. |
розр. |
розр. |
розр. |
розр. |
розр. |
розр. |
розр. |
Контрольні запитання
1.Що називається моментом інерції тіла?
2.Сформулювати теорему Штайнера.
3.Вивести формулу для моменту інерції однорідного диска.
4.Вивести формулу для періоду коливань крутильного маятника.
5.Чому для експериментального визначення моменту інерції крутильного маятника необхідне додаткове навантаження його тілами правильної ґеометричної форми?
6.Вивести формулу для визначення моменту інерції крутильного маятника.
Рекомендована література
1.Курс фізики / За ред. І.Є. Лопатинського. – Львів: Вид-во “Бескид Біт”, 2002.
2.Трофимова Т.И. Курс физики. – М.: Высш. шк., 1990.
3.Савельев И.В. Курс общей физики. Т. 1. – М.: Наука, 1982.
94

Лабораторна робота № 9
ВИЗНАЧЕННЯ МОМЕНТУ ІНЕРЦІЇ ТІЛА НЕПРАВИЛЬНОЇ ГЕОМЕТРИЧНОЇ ФОРМИ
95
Інструкції до лабораторних робіт
Мета роботи
Використовуючи крутильний маятник, визначити момент інерції тіла неправильної ґеометричної форми.
Прилади та обладнання
Крутильний маятник, тіло неправильної ґеометричної форми, секундомір, штанґенциркуль.
Опис вимірювального пристрою
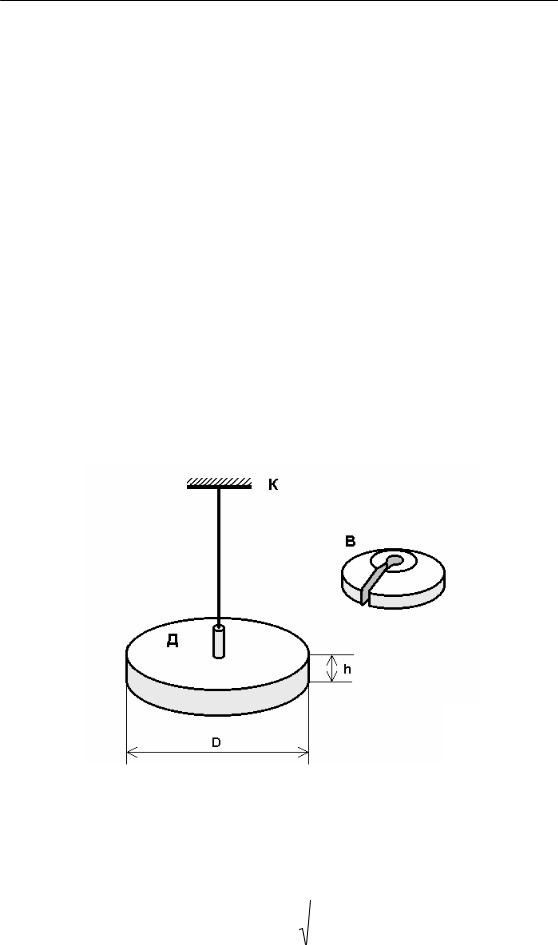
Крутильний маятник складається з вертикальної дротини, нерухомо закріпленої верхнім кінцем в кронштейні К і горизонтального однорідного суцільного диска Д, закріпленого в центрі до нижнього кінця дротини. На диск можна накладати тіло неправильної ґеометричної форми B так, що вісь маятника проходитиме через центр мас тіла (рис. 1).
Рис. 1
Виведення розрахункової формули
Період коливань ненавантаженого тілом B крутильного
маятника описує формула: |
|
|
|
|
|
|
T = 2π |
J0 |
, |
(1) |
|||
|
||||||
1 |
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
96 |
|
|
|
|
|

Лабораторна робота №9
де |
f – модуль кручення дротини, |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
J0 – момент інерції маятника. |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
J0 достатньо точно можна визначити як момент інерції |
|||||||||||||||||||
суцільного диска Д: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
æ D ö |
2 |
1 |
|
2 |
|
1 |
|
2 |
|
1 |
|
4 |
|
|
|||
|
J0 = |
|
mç |
|
÷ |
= |
|
|
mD |
|
= |
|
ρVD |
|
= |
|
πρD |
|
h, |
(2) |
|
2 |
|
8 |
|
|
8 |
|
32 |
|
|||||||||||
|
|
è |
2 ø |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
де |
m = ρ V – маса диска (ρ - густина матеріалу диска); |
|
||||||||||||||||||
V = 41 πD2h - об’єм диска (D, h – діаметр і висота диска).
Період коливань маятника, навантаженого тілом B:
T2 = |
2π |
|
J0 |
+ J |
, |
|
(3) |
||||||
|
|
f |
|
|
|
||||||||
де J – момент інерції тіла B. |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
Шляхом нескладних перетворень з (1) і (3) можна одержати: |
|
||||||||||||
|
|
|
|
T2 |
- T2 |
|
|
|
|
|
|||
J = J |
0 |
|
2 |
|
1 |
, |
|
(4) |
|||||
|
|
|
|
||||||||||
|
|
|
|
|
T2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
а врахувавши (2), – кінцевий вираз для визначення J: |
|
||||||||||||
|
1 |
πρD4h |
T2 |
|
|
- T2 |
|
||||||
J = |
|
2 |
|
|
1 |
. |
(5) |
||||||
32 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
T2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
При підготовці до виконання роботи використати: Теоретична частина. Розділи 1.1, 3.5.
Послідовність виконання роботи
1.Виміряти у трьох різних напрямах діаметр диска D.
2.Виміряти у трьох різних місцях висоту диска h.
3.Привести систему в коливальний рух, закрутивши маятник на кут не більше 90° і виміряти час t1 десяти повних
коливань.
Визначити період Т1 за формулою:
T1 = 10t1 .
97

Інструкції до лабораторних робіт
4.Навантажити маятник тілом B і аналогічно до п. 3 визна-
чити період коливаньТ2. Вимірювання періодів, зазначені в п. 3 і п. 4, провести по три рази.
5.Результати вимірювань записати в таблицю; Перевівши результати вимірювань всіх величин в одиниці СІ, за формулою (5) розрахувати J.
6.Визначити абсолютну і відносну похибки.
густина матеріалу диска ρ = ( 1,40 ± 0,005 )103 кг/м3.
Таблиця результатів вимірювань
№ |
D, |
D, |
h, |
h, |
Т1, |
ΔТ1, |
Т2, |
ΔТ2, |
|
мм |
мм |
мм |
мм |
с |
с |
с |
с |
||
|
|||||||||
1 |
вимір. |
розр. |
вимір. |
розр. |
розр. |
розр. |
розр. |
розр. |
|
2 |
вимір. |
розр. |
вимір. |
розр. |
розр. |
розр. |
розр. |
розр. |
|
3 |
вимір. |
розр. |
вимір. |
розр. |
розр. |
розр. |
розр. |
розр. |
|
сер. |
розр. |
розр. |
розр. |
розр. |
розр. |
розр. |
розр. |
розр. |
Контрольні запитання
1.Що називається моментом інерції тіла ?
2.Вивести формулу для моменту інерції однорідного диска.
4.Вивести формулу для періоду коливань крутильного маятника.
7.У чому полягає методика визначення моменту інерції тіла неправильної ґеометричної форми з застосуванням крутильного маятника?
8.Вивести формулу для визначення моменту інерції тіла неправильної ґеометричної форми.
Рекомендована література
1.Курс фізики / За ред. І.Є. Лопатинського. – Львів: Вид-во “Бескид Біт”, 2002.
2.Трофимова Т.И. Курс физики. – М.: Высш. шк., 1990.
3.Савельев И.В. Курс общей физики. Т. 1. – М.: Наука, 1982.
98

Лабораторна робота № 11
ВИЗНАЧЕННЯ МОДУЛЯ ПРУЖНОСТІ МЕТОДОМ ЗГИНУ
99
Інструкції до лабораторних робіт
Мета роботи
Визначити модуль пружності методом згину.
Прилади та обладнання
Вимірювальний пристрій, тягарці, масштабна лінійка, штанґенциркуль.
Опис вимірювального пристрою
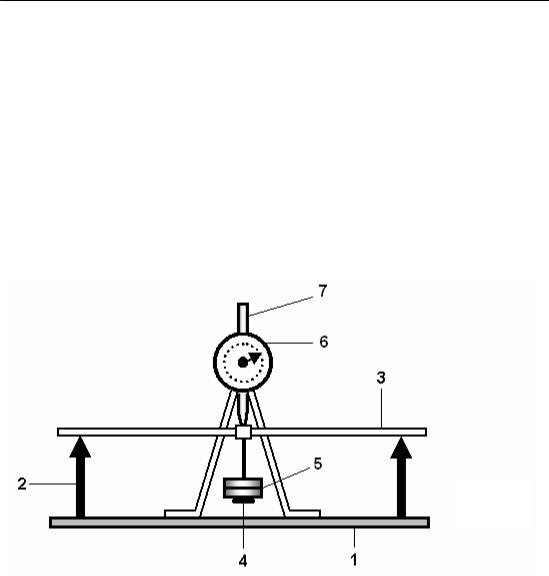
Рис. 1
До масивної основи (1) прикріплені стояки (2), верхня частина яких закінчується тригранними призмами. Горизонтальні верхні ребра призм є опорами досліджуваного стрижня (3).
На підставку (4), підвішену посередині до стрижня (3), можна накладати тягарці (5). Прогин навантаженого тягарцями стрижня вимірюється індикатором годинникового типу (6) з точністю до 0,01 мм. Індикатор фіксується у спеціальному гнізді на кронштейні (7); кронштейн прикріплений до середини основи (1).
Виведення розрахункової формули
Розглянемо стрижень прямокутного перерізу, що лежить симетрично на двох тригранних призмах, відстань між якими становить L (рис. 2). До центра стрижня прикладена вертикально вниз сила F.
Під дією цієї сили нижні шари стрижня зазнають пружної деформації розтягу, а верхні шари – деформації стиску; при цьому
100
