
DataBase_lecture2
.pdfПриклад 6.3. Групове поле може зображати таке значення як Адреса(Індекс, Місто, Вулиця, будинок, Квартира). В той же час утворення групи виду ХХХ(Прізвище, Дата покупки, Факультет) є некоректним з точки зору інтерпретації такого поєднання полів.
Тема 7. Логічні моделі баз даних. Види логічних моделей даних
A. Теоретичні відомості
Логічна модель бази даних визначає способи побудови та застосування структури даних в конкретному технологічному середовищі. Теоретично, таких способів може бути запропоновано безліч. Але, оскільки будь яка пропозиція завершується розробкою засобів
систем і технологій які її реалізують, то протягом останніх десятиріч сформувалося лише декілька напрямів вирішення цієї категорії проблем. До класичних способів побудови логічної структури відносять ієрархічну, мережеву та реляційну моделі.
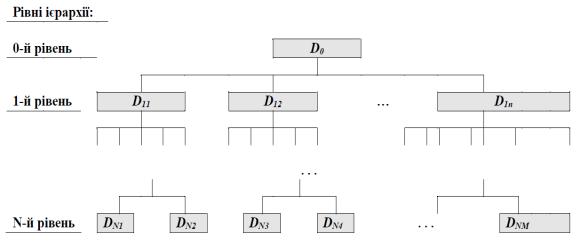
Ієрархічна модель запропонована в 1964 р. в СУБД IMS/360 фірми IBM. Модель передбачає впорядкування даних за принципом ієрархії:
всі одиниці даних класифікуються за рівнями ієрархії;
до найвищого рівня ієрархії входить лише один елемент;
зв'язки встановлюються лише між елементами сусідніх рівнів з підпорядкуванням від вищого до нижчого;
кожен елемент нижчого рівня пов'язується лише з одним елементом вищого рівня;
елемент початкового рівня ієрархії не може підпорядковуватися жодним іншим одиницям;
елементи останнього рівня ієрархії не мають підпорядкованих елементів даних.
Ієрархічна модель дозволяє використання лише зв'язків типу 1:1 та 1:N. Схема зв'язків між даними в ієрархічній моделі може бути зображена у вигляді деревовидного графу.
Рис 7.1. Ієрархічна модель даних
Мережева модель запроваджена в 1969 р. за пропозицією і концепцією Data Base Task Group (DBTG) і реалізована в однойменній СУБД. Мережеву структуру розглядають як узагальнення ієрархічної за рахунок зняття обмежень на класифікацію одиниць даних та встановлення зв'язків між ними. Ця модель розглядає всі елементи даних як рівноцінні та дозволяє визначення довільної кількості зв'язків довільного характеру. Описати схему зв'язків можна у вигляді мережевого графа.
Реляційна модель – запропонована в 1971 р. Е. Коддом (E. Codd) в якості однієї з альтернатив у розв'язанні проблем створення та опрацювання баз даних великих об'ємів. Принциповим моментом реляційної моделі є застосування табличного способу подання даних. Таблиця в свою чергу є зовнішнім зображенням відношення (relation) засобу поєднання значень з кількох множин. Перевагами реляційної моделі є:
простота та природність табличної форми зображення даних;
незалежність методів та процедур опрацювання від обсягів баз даних;
можливість визначення зв'язків між даними через самі дані;
наявність теоретичного обґрунтування методів та технологій роботи з реляційними базами даних.
На сьогодні більшість технологій та систем управління базами даних реалізовані на основі реляційної моделі.
Похідними від класичних моделей є адаптивна та нерегулярні моделі.
Адаптивна модель підтримується в сімействі СУБД ADABAS, що випускається фірмою Software AG, і поєднує в собі можливості класичних моделей, а саме:
база даних може бути побудована за принципами ієрархічної, мережевої чи реляційної моделі;
в одній базі даних можуть бути реалізовані сегменти, побудовані за різними моделями;
ті ж самі дані можуть зображатися опрацьовуватися за принципами різних моделей, в залежності від потреби.
Нерегулярні моделі не є ієрархічними, мережевими, чи реляційними але можуть використовувати їх принципи та методи. Такі моделі застосовуються для реалізації вузькоспеціалізованих, специфічних застосувань в яких неможливо достатньо адекватно відобразити особливості предметної області за допомогою класичних моделей. Розробка баз даних за нерегулярними моделями передбачає розробку засобів їх підтримки.
Перспективними моделями є моделі, які розвивають принципи реляційної – постреляційна, багатовимірна, об'єктно-реляційна.
Постреляційна модель є узагальненням реляційної, що передбачає застосування в клітинках таблиці неелементарних значень – масивів, множин, груп, таблиць, тощо.
Багатовимірна модель розширює кількість вимірів з двох (в класичній реляційній моделі) до трьох та більше. Така модель є, в першу чергу, моделлю опрацювання, а не зберігання даних.
Об'єктно-реляційна модель розвиває класичну реляційну за рахунок застосування методів об'єктно-орієнтованих технологій. Зокрема, в такій моделі таблиця розглядається як клас, рядки або стовпчики - як об'єкти, значення даних – як значення властивостей, з кожним об'єктом пов'язується множина методів, і т.д. Для елементів такої моделі характерні класичні
властивості об'єктно-орієнтованого підходу, зокрема, наслідування та інкапсуляція.
B. Приклади
Приклад 7.1. За принципами ієрархічної моделі може бути побудована база
даних , яка містить відомості про організаційну структуру університету.
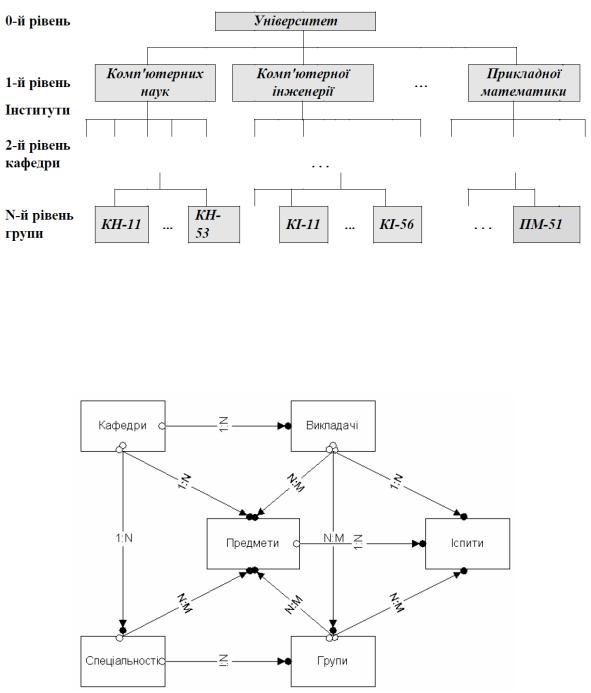
Рис 7.2. Приклад структури бази даних побудованої за ієрархічної моделлю
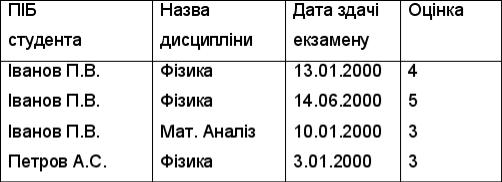
Приклад 7.2. Прикладом мережевої структури бази даних є база даних навчального процесу, в якій зберігаються відомості про такі об'єкти як Кафедри, Спеціальності, Викладачі, Предмети, Групи, Іспити. Схема зв'язків та їх типи при цьому можуть бути визначені довільно.
Рис 7.3. Приклад структури бази даних побудованої за мережною моделлю
Приклад 7.3. В реляційній моделі баз даних застосовується таблична форма зображення даних, а зв'язки між такими табличними структурами підтримуються через відповідність значень самих даних

Рис 7.4. Приклад структури бази даних побудованої за реляційною моделлю
Додаток1. Організація баз даних. КІ-3.
Основи реляційної алгебри
Реляційна модель баз даних надає можливість маніпулювати над доменами відношень. Для цих цілей існує два види апарата маніпулювання відношеннями: реляційна алгебра (алгебра відношень) і реляційне обчислення (обчислення відношень).
Алгеброю відношень називають систему операцій маніпулювання відношеннями, кожний оператор якого в якості операнда (операндів) використовує одне чи більше відношень і утворює нове відношення по попередньо обумовленому правилу.
Реляційне обчислення дозволяє шляхом використання обчислення предикатів та кванторів змінних описувати відношення та операції над ними в вигляді аналітичного виразу або формули.
В реляційній алгебрі використовують п'ять основних операцій: об'єднання, різниця, декартовий добуток, проекція і селекція.
1.Проекція .Суть цієї операції полягає в тому, що береться відношення R, видаляються деякі з його компонентів і перевпорядковуються компоненти, що залишились. Якщо в результаті проекції появляються однакові кортежі, то вони з результуючого відношення вилучаються.
Операція проекції полягає в виділенні необхідних стовпців (доменів) з відношення .
Нехай дано відношення СТУДЕНТ-УСПІШНІСТЬ.
Таблиця 1. СТУДЕНТ-УСПІШНІСТЬ
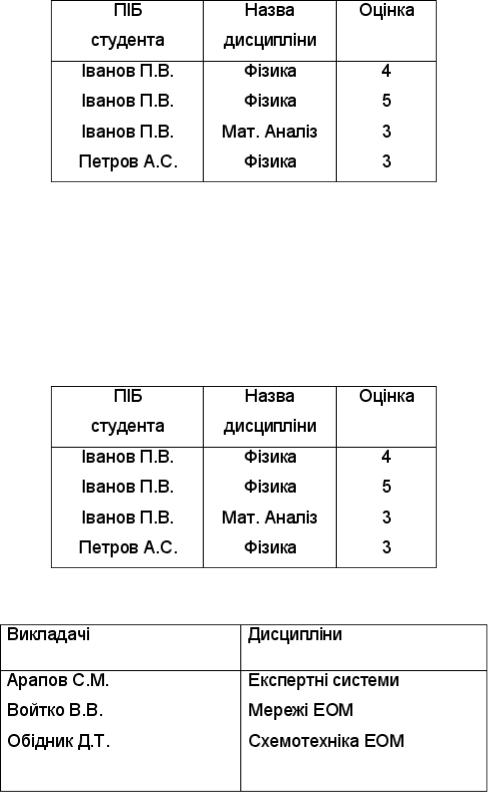
В результаті виконання операції проекції отримуємо нове відношення, яке представлено в табл. 2.
Таблиця 2. Приклад операції "проекція"
2. Об'єднання. Об'єднання відношень R і S (позначаться RИS) представляє собою множину кортежів, які належать R чи S або їм обом. Оператор об'єднання застосовується тільки до відношень однакової арності. Якщо в результаті об'єднання відношень мають місце однакові кортежі, то вони заміняються одним.
Нехай задано два відношення , представлені таблицями 3, 4. Виконаємо над ними операцію об'єднання.
Таблиця 3. ВИКЛАДАЧІ-ДИСЦИПЛІНИ
Таблиця 4. ВИКЛАДАЧІ-ДИСЦИПЛІНИ
В результаті об'єднання відношень отримуємо результуюче відношення, яке представлено в табл.5.
Таблиця 5. ВИКЛАДАЧІ-ДИСЦИПЛІНИ
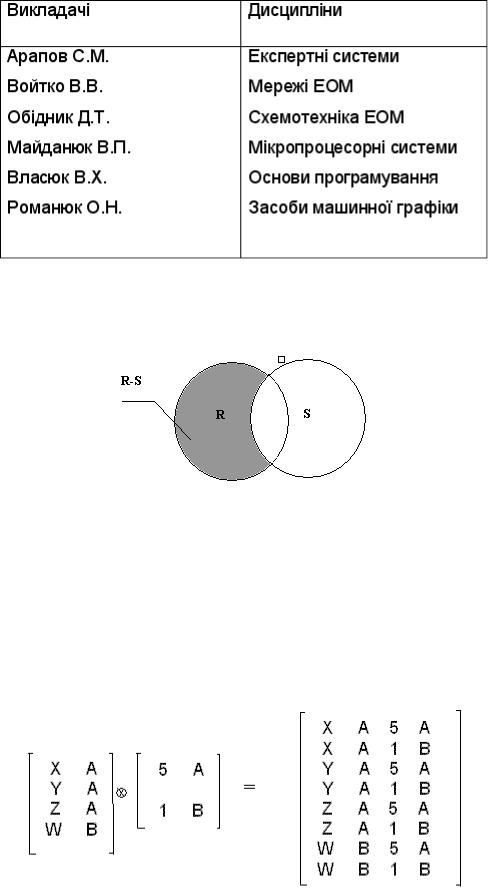
3.Різниця. Різницею відношення R і S( позначається як R-S), називається множина кортежів, які належать R, але не належать S (рис.1.). При реалізації різниці необхідно, щоб R і S мали одну і ту ж саму арність.
Рисунок 1 -Графічна ілюстрація операції віднімання відношень
Якщо А - відношення про жителів мікрорайону, В- відношення про тих, хто пройшов медичний огляд, то відношення А-В буде містити дані про тих жителів мікрорайону, хто не пройшов медичний огляд.
4. Декартовий добуток. Нехай R і S - відношення арності k1 і k2 відповідно. Тоді декартовим добутком відношень R і S називається множина кортежів довжини k1 + k2, перші k1 компонентів яких утворюють кортежі, які належать R, а останні k2 - кортежі, що належать S. Наприклад :
Результатом декартового добутку відношень СТУДЕНТИ (Табл. 6 ) та ЕКЗАМЕНИ (Табл. 7 ) буде відношення ЕКЗАМЕНАЦІЙНА ВІДОМІСТЬ (Табл. 8).
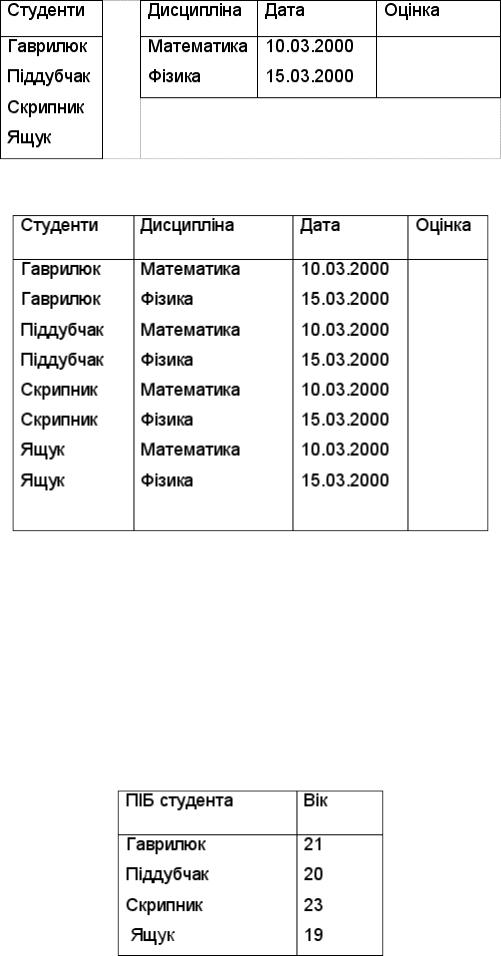
Таблиця 6---------------------- |
Таблиця 7 СТУДЕНТИ - ЕКЗАМЕНИ |
Таблиця 8. ЕКЗАМЕНАЦІЙНА ВІДОМІСТЬ
5. Селекція. Нехай F - формула, яка може бути утворена слідуючими засобами: а) операндами, які є константами чи номерами компонентів; б) арифметичними операторами порівняння <, =",">, №, і; в) логічними операторами Щ(І), Ъ(АБО), Ш(НІ).
В цьому випадку df (R) є множена кортежів t , які належать R, таких, що при підстановці i-го компонента t замість будь-якого входження номера i в формулу F для всіх i вона стане істиною.
Наприклад, d2>3 (R) означає множину кортежів, що належать R, другий компонент яких більше третього компонента.
Таблиця 9
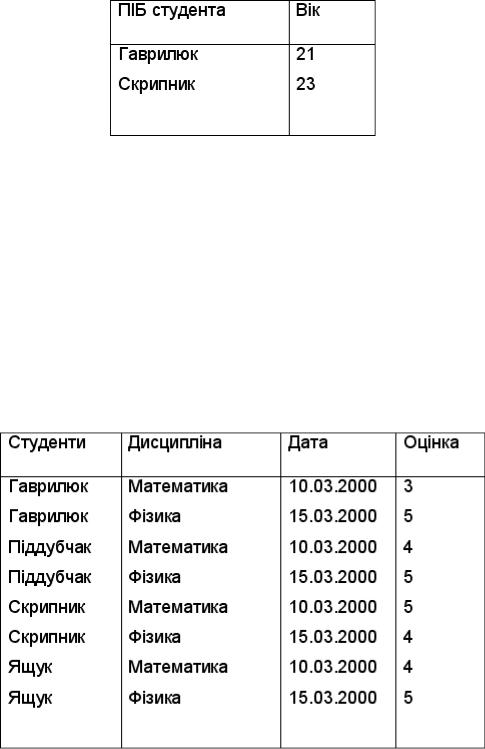
При реалізації селекції відношення, приведеного в табл.9 ,згідно ознаки ( вік>20) ,отримуємо відношення
Таблиця 10
Крім перерахованих операцій існують і інші, але всіх можна отримати з п'яти основних.
Розглянемо неосновні операції перетину та ділення.
Перетин R S двох відношень R та S знаходиться згідно формул R-(R-S).
Нехай R та S є відношення арності r і s відповідно, де r > s і S . Тоді частка R S є множина кортежів t довжини (r -s) таких, що для всіх кортежів u довжини s, які належать S, кортеж tu належить R.
Виконаємо операцію ділення над відношеннями, які представлені відповідно таблицями 11
та 12.
Таблиця 11. Екзаменаційна відомість
Таблиця 12
