53

уравнения Шредингера в прямоугольном потенциальном ящике с размерами d ×w ×L имеет вид

где n,l,m = 1,2,3... – квантовые числа, а соответствующие волновые функции представляются произведением периодической части блоховской функции u(~r) и огибающих функций для квантовых ям в направлениях x,y и z.

Кроме технологических путей создания структур с пониженной размерностью электронного газа, локализация электронов осуществляется также в магнитном поле. С помощью сильного магнитного поля моделируется лазерный режим в квантовых проволоках и ячейках. При помещении обычного лазерного диода в продольное магнитное поле реализуется структура, аналогичная квантовой проволоке. Если используется активный слой в виде квантовой ямы, а магнитное поле ориентировано перпендикулярно плоскости гетероперехода, то образуются квантовые ячейки.

В1987 г. сообщено о получении гетероструктур типа квантовых ячеек, люминесцирующих при инжекции носителей тока. Размеры ячеек составляли 150 ×1000 ×1000˚A в системе GaInAsP −InP. В импульсном режиме при 77 К в плоскости решетки квантовых ячеек наблюдалось усиление света.

Результаты последних исследований свидетельствуют о тесной связи новейших достижений полупроводниковой техники с изучением фундаментальных физических процессов в гетероструктурах. Квантоворазмерные эффекты – основа разработки новых уникальных приборов полупроводниковой электроники.

2.2.Уровни энергии подзон и частота генерации

Влазерном режиме усиление в активной области компенсирует потери излучения, связанные с его выходом из резонатора, с рассеянием и дифракцией в оптическом волноводе. Генерация развивается на частотах, соответствующих максимуму усиления. В квантоворазмерных лазерах частота генерации определяется прежде всего положением уровней подзон, между которыми осуществляются оптические переходы.

Впростейшем случае квантование движения носителей тока в квантовой яме рассматривается как поведение электрона в прямоугольной потенциальной яме. Энергетический спектр усложняется в сверхрешетках, когда ширина потенциальных барьеров сравнима с размерами квантовых ям и надо учитывать взаимодействие уровней в отдельных ямах.

54

Рис. 2.3. Изменение ширины запрещенной зоны Eg в точках Γ, L и X зоны Бриллюэна с составом x соединения AlxGa1−xAs: Γ - Eg(x) = 1.425+1.155x +

0.37x2 (эВ); L - Eg(x) = 1.734 + 0.574x + 0.055x2 (эВ); X - Eg(x) = 1.911 + 0.005x + 0.245x2 (эВ).

В лазерах на основе AlxGa1−xAs высота потенциальных барьеров в квантовых ямах практически линейно связана с составом x. В точке Γ зоны Бриллюэна ширина запрещенной зоны Eg при изменении состава соединения AlxGa1−xAs зависит от x при 300 К как Eg(x) = 1.425 + 1.155x + 0.37x2 (эВ). При этом прямозонная структура реализуется до x ≈ 0.4, а при больших содержаниях Al дно зоны проводимости переходит в точку симметрии X (рис.2.3). Достаточно хорошим приближением в области прямозонной структуры служит выражение Eg(x) = 1.424 + 1.247x (эВ). Тогда, если x = xb −x0, где x0 и xb - молярное содержание Al в активной области и барьерных слоях соответственно, то скачки в зонах составляют Ec = 0.848 x эВ и Ev = 0.399 x эВ.

Для учета изменения величины эффективных масс носителей с составом соединения AlxGa1−xAs можно использовать линейную интерполяцию между GaAs и AlAs. Тогда для эффективной массы электронов на дне зоны проводимости в точке симметрии Γ получаем mc = (0.067 + 0.083x)me. Для дырок надо различать тяжелые и легкие дырки и учитывать анизотропию эффективных масс. Для оценок обычно используются результаты расчетов зонной теории. Значение эффективной массы тяжелых дырок для плотности состояний принимается равным mvh = (0.62 + 0.14x)me, а средняя величина эффективной массы легких дырок составляет mvl = (0.087 + 0.063x)me.

55

Анизотропия энергетического спектра дырок вблизи потолка валентной зоны полностью характеризуется известными зонными параметрами Люттинжера γ1,γ2 и γ3 или Дрессельхауза, Кипа и Киттеля A,B и C. Для сферических зон выполняется γ2 = γ3 или C = 0. В терминах параметров Люттинжера для полупроводников со структурой алмаза или цинковой обманки компонент эффективной массы тяжелых дырок (проекция момента импульса jz = ±3/2) составляет, например, в направлении кристаллографических осей [100] величину mvh = me/(γ1 −2γ2). Компонент для легких дырок (проекция момента импульса jz = ±1/2) равен mvl = me/(γ1 +2γ2). В на-

ким дыркам.

В квантовых ямах вырождение по тяжелым и легким дыркам снимается. Положение уровней подзон в каждой системе дырок определяется величиной продольного компонента эффективной массы соответствующих дырок. Если квантоворазмерные слои выращиваются в плоскости (100), то для продольных масс дырок можно принять значения mvh = me/(γ1 − 2γ2) и mvl = me/(γ1 + 2γ2). Поперечные компоненты эффективных масс дырок

составляют при этом mvh = me/(γ1 + γ2) и mvl = me/(γ1 − γ2). Эти значения задают закон дисперсии дырок в плоскости квантоворазмерных сло-

ев и плотность их энергетических состояний. Смешение состояний и спинорбитальное взаимодействие приводят к непараболичности валентных зон и усложняют кривые дисперсии дырок.

Набор параметров Люттинжера для GaAs γ1 = 6.8, γ2 = 1.9 и γ3 = 2.73 дает следующую величину эффективных масс тяжелых и легких дырок в направлении [100]: mvh = 0.34me и mvl = 0.094me. В направлении [111] реализуются значения mvh = 0.75me и mvl = 0.082me. Анизотропия тяжелых дырок заметно изменяет положение уровней подзон валентной зоны в зависимости от ориентации квантоворазмерных слоев.

Поскольку положение уровней подзон в квантовых ямах задается продольной массой носителей тока, то спектральный диапазон для переходов между подзонами с испусканием или поглощением света определяется именно этим компонентом эффективной массы. С законом дисперсии носителей, т.е. поперечным компонентом эффективной массы, связана скорость оптических переходов и поэтому – форма спектров испускания и поглощения. Например, для переходов с сохранением квазиимпульса электрона поперечные массы носителей прямо входят через приведенную массу mri в приведенную плотность состояний. Однако граничные частоты νni одно-

56

значно задаются продольной массой носителей тока и в случае прямых переходов соответствуют максимумам в спектрах люминесценции и усиления.

Сперва проведем оценки частот генерации в квантоворазмерных гетеролазерах в приближении изотропной эффективной массы [10]. В пределе достаточно больших потенциальных барьеров имеем

Здесь все значения относятся к узкозонному материалу и зависят от его компонентного состава. Например, для AlxGa1−xAs в активной области лазера значение Eg, mc и mvi практически линейно возрастают с увеличени-

ем x - молярной доли AlAs. Приводя (2.9) к численному виду, получаем hνni = Eg + 3.76 × 10−3n2(100/d)2(me/mri) (эВ), где d задается в ˚A, а mri -

приведенная масса с учетом соответствующих дырок.

Из формулы (2.9) следует, что одна и та же частота генерации может быть реализована в лазерах с разным составом активной области путем подбора толщины d или при перескоке генерации на переходы через высоколежащие подзоны. При уменьшении d до 50˚A и одновременном увеличении x в активной области до 0.2 энергию квантов света hνg для генерации на переходах с участием легких дырок 1010 можно поднять на 580 мэВ относительно GaAs. Это выполняется, если созданы достаточно большие потенциальные барьеры на границах квантовой ямы.

Квантоворазмерный эффект отражается на частоте генерации заметнее с уменьшением ширины активной области d и эффективной массы носителей. Для разных материалов значение эффективной массы электронов колеблется от 0.015me(InSb) до 0.28me(ZnS), соответственно изменяется приведенная масса mri. Оценки по формуле (2.9) служат первым приближением для определения частоты генерации νg. Они дают, как правило, завышенные значения энергии генерируемых квантов hνg.

При учете влияния высоты потенциальных барьеров на положение уровней подзон в квантовой яме и частоту генерации начальные уровни подзон находятся из уравнения вида (2.2). С уменьшением высоты потенциальных барьеров U0 в квантовой яме остаются только уровни с n = 1. Граничное значение U0 = Un для выхода уровней подзоны с квантовым числом n за пре-

Здесь Ecn∞ – положение начальных уровней подзоны с квантовым числом n в

57

Рис. 2.4. Номограмма для расчета Ecn относительно Ecn∞ в зависимости от отношения Ecn∞ /U0. Цифры на кривых – значения квантового числа n.

случае бесконечно больших потенциальных барьеров, которое определяется (2.3). Аналогично записывается условие выхода из квантовой ямы уровней размерного квантования для дырок. Для уровней с n = 2 имеем соответственно U2 = Ec∞2/4 и U2 = Evi∞2/4. Условия жестче для электронов и легких дырок. Например, в системе GaAs − Al0.3Ga0.7As уже при d = 50 ÷ 60˚A из квантовой ямы выходят уровни электронов и легких дырок с n = 2. Еще раньше выходят уровни с n ≥ 3.

Трансцендентное уравнение (2.2) аналитически не решается. Поэтому удобно пользоваться номограммой, связывающей значение уровня Ecn в квантовой яме относительно величины Ecn∞ для бесконечно больших потенциальных барьеров с отношением Ecn∞ к высоте барьеров U0 (рис.2.4). Значение Ecn∞ легко рассчитать по формуле (2.3). Аналогичная номограмма получается для дырок в квантовой яме. Поскольку для типичных лазерных систем (например, GaAs −Al0.3Ga0.7As) отношение Ec1/U0 при d ≈ 100˚A составляет порядка 0.2, то отличие Ec1 от приближенного значения Ec∞1 достигает 40%. Такая же ошибка возникает при расчете уровней по формуле вида (2.3) для легких дырок. Гораздо точнее формула (2.3) определяет уровни подзон для тяжелых дырок.

Чтобы привести уравнение (2.2) к аналитической форме, воспользуемся представлением правой части уравнения в виде гипергеометрической функции и ограничимся начальными членами ее разложения в ряд. В ре-

58

Рис. 2.5. Сравнение точного решения уравнения (2.2) (сплошные кривые) и расчетов Ecn по формуле (2.11) (штриховые кривые). Цифры на кривых – значения квантового числа n.

зультате приходим к формуле

Расчеты Ecn по этой формуле дают такие же значения, как точное решение (2.2) на рис.2.4. В более широком интервале сравнение расчетов Ecn по формуле (2.11) с точным решением уравнения (2.2) показано на рис.2.5. Как видно, вплоть до значений Ecn∞ /U0 ≤ 2 выражение (2.11) хорошо описывает Ecn. Ошибка не превышает 16% .

Таким образом, для энергии генерируемых квантов при учете конечной высоты потенциальных барьеров в квантовой яме получаем выражение

водимости и валентной зоне соответственно. В предельном случае больших потенциальных скачков формула (2.12) сводится к (2.9).

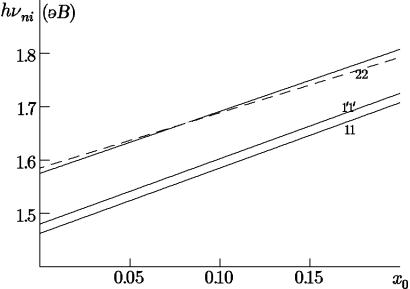
Пример расчета hνg = hνni по уточненной формуле (2.12) представлен на рис.2.6 для двух вариантов, когда фиксируется состав в барьерных слоях (xb = 0.4) или поддерживается постоянной разница x = xb − x0 при изменении состава x = x0 в активной области. Максимальный сдвиг hνg относительно Eg в GaAs достигается на переходах 22 при уменьшении d до

60

Рис. 2.7. Параметры огибающей волновой функции электронов λn (сплошные кривые) и C2 (штриховые кривые) в зависимости от положения уровней подзон в квантовой яме. Цифры на кривых – значения квантового числа n.

где огибающая волновая функция записывается в виде (n = 1,2,3...)

стемах с достаточно большими барьерами для нижних подзон выполняется λn/d ≈ (1/2πn) pEcn/U0. При этом амплитудный коэффициент огибающей волновой функции C2 связан с λn выражением C2d/2 ≈ 1 −4λn/d. При сравнимых Ecn и U0 параметр λn приближается к d, а C2 падает до нуля (рис.2.7).

Следующее уточнение положения уровней подзон в квантовой яме связано с различием эффективных масс носителей в самой яме и барьерных слоях. Тогда необходимо дополнительно использовать условие непрерывности величины (1/mc)dϕn/dz на границе квантовой ямы и барьерных слоев. Решение уравнения Шредингера снова имеет стандартный функциональный вид (2.14), где несколько изменяется запись нормировочных коэффициентов δ и C2 в барьерных слоях, а в выражении для æ вместо mc стоит mcb

61

– эффективная масса электронов в эмиттере. Собственные значения энергии электронов находятся из уравнения

Обычно mcb > mc, поэтому уровни оказываются ниже из-за "утяжеления"квазичастиц в результате проникновения волновых функций в барьерные слои. Хорошим приближением (2.15) служит выражение

Ошибка при расчетах по формуле (2.16) для Ecn∞ ≤ U0 составляет менее 11%. Причем, когда mcb ≤ mc, то результат оказывается завышенным, а при mcb ≈ 2mc – заниженным.

Используя (2.16), получаем аналитическую формулу для частоты генерации:

При mcb = mc и mvib = mvi (2.17) переходит в (2.12). В системе GaAs −AlGaAs учет скачков эффективных масс носителей на границах квантовых ям приводит к уменьшению значения hνg. При толщинах 50 − 100˚A сдвиг hνg для переходов 11 и 22 составляет 6–14 мэВ.

В лазерных сверхрешетках необходимо учитывать близость квантовых ям друг к другу. Тогда при сшивании огибающих волновых функций ϕn(z) используются периодические граничные условия для значений ϕn(z) и (1/mc)dϕn/dz. Учет конечной толщины барьерных слоев D показывает, что с уменьшением D состояния в квантовой яме, описываемые четными огибающими волновыми функциями (n = 1,3...), опускаются, а состояния с нечетными волновыми функциями (n = 2,4...) поднимаются. Для этих состояний условия выхода из квантовой ямы смягчаются. Собственные значения энергии удовлетворяют уравнению

выполняется æ0D ≈ π.