1.3. Додавання двійкових чисел у модифікованому оберненому коді

Реалізується так само, як і в доповняльному коді. Обернені коди чисел додаються порозрядно, знакові розряди додаються як розряди цілих чисел. Суму отримуємо у оберненому коді.

Відмінність полягає у тому, що одиницю переносу із старшого знакового розряду, якщо вона з’являється, потрібно додати до молодшого розряду суми, тобто виникає циклічний перенос.

Приклад 2. Додати у модифікованому оберненому коді числа А і В при умові:

1) А > 0; B < 0; A + B > 0.

A = + 0,1101; B = - 0,0001; +

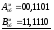
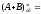100,1011

Циклічний перенос ↳→→+1

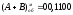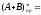; 00,1100;

2) А < 0; B < 0; A + B < 0.

A = - 0,1101; B = - 0,0001; +

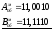
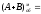111,0000;

Циклічний перенос ↳→→+1

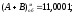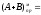; 11,1110;

1.4. Переповнення розрядної сітки при додаванні у модифікованих машинних кодах

Переповнення розрядної сітки при додаванні модифікованих кодів, так само як і при додаванні у звичайних кодах із фіксованою комою, може бути лише у випадках, коли доданки мають однакові знаки. Таке переповнення виявляється способом порівняння знакових розрядів отриманої суми, наприклад, застосовуючи операцію додавання за модулем 2 (XOR). Ознакою переповнення є неспівпадання цифр, які створюються у двох знакових розрядах суми, тобто код знаку числа має вигляд 01 або 10. Відповідно, результат неможливо віднести до жодного з модифікованих кодів. Пояснимо це на наступних прикладах.

Приклад 3:

1. А = + 0,1101; 2. А = - 0,1101;

В = + 0,0111; В = - 0,0111;

А + В > 0; А + В < 0;

++

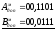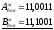
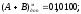
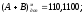
Відкидається 

Як видно з прикладів, у знакових розрядах отриманої суми додатних доданків маємо комбінацію „01”, від’ємних – „10”, які свідчать про переповнення розрядної сітки.

\

1.1. Подання чисел з рухомою комою

У форматі з рухомою комою, який звичайно називають нормальною формою запису, числа записуються наступним чином:

A =  М * d ^{ Р} ,

де p – ціле число, яке називається порядком числа А;

d – основа системи числення;

М – мантиса числа А (звичайно |M| < 1).

При нормальній формі запис одного числа може приймати різний вигляд у залежності від обмежень, що накладаються на його форму. Фактично місце коми у мантисі М визначається величиною порядку р. Із зміною порядку р у більшу або меншу сторону кома відповідно переміщується ліворуч або праворуч, тобто рухається (“плаває”) у зображені числа.

Наприклад: 234₁₀ = 0,234 * 10³ = 0,0234 * 10⁴ = 2,34 * 10² ;

101101₂ = [0,101101 * (10)¹¹⁰ = 0,00101101 * (10)¹⁰⁰⁰ ]₂ .

Можна зауважити, що хоча числа у наведених прикладах однакові за абсолютною величиною, проте мантиса потребує різної кількості розрядів. Для цього, щоб запобігти цьому, звичайно уводять деякі обмеження. Найбільш розповсюдженим і зручним для подання у комп’ютерах обмеженням є наступне:

d^-1  M  1.

Числа, що записані у такій формі називаються нормалізованими. Іншими словами, у нормалізованих числах у мантисі першою цифрою стоїть 0, а перша цифра після коми – це цифра відмінна від нуля. Для двійкової системи числення вона дорівнює 1.

Таким чином, мантису розглядають як число менше одиниці, а порядок – як ціле число.

Операція нормалізації виконується шляхом зсуву мантиси і відповідного зменшення або збільшення порядку на величину, яка дорівнює кількості розрядів, на яку була зсунута мантиса.

Приклад: нормалізувати наступні числа:

0,00237 * 10⁵ = 0,237 * 10³ – мантиса зсувається на два розряди вліво, тобто – збільшується, а порядок зменшується на дві одиниці.

10101,011₂ * 10¹⁰ = 0,10101011 * 10 ¹¹¹ - мантиса зсувається вправо на 5 розрядів, тобто – зменшується, а порядок збільшується на 5 одиниць.

Нормалізоване подання чисел дозволяє зберігати у розрядній сітці більшу кількість цифр, що мають значення, тому точність обчислень підвищується. Зазвичай у комп’ютерах нормалізація здійснюється автоматично як при вводі чисел, так і у процесі обчислень (після виконання чергової операції). При цьому мантиса зсувається ліворуч на необхідну кількість розрядів і виконується відповідне зменшення порядку, тобто виконується “нормалізація вліво”.

При виконанні операції додавання або віднімання нормалізованих чисел з різними порядками одно з них “денормалізується” до вирівнювання порядків, а сума (або різниця) знову нормалізується.

У розрядній сітці комп’ютерів фіксуються знак числа, знак порядку, порядок числа і числовий вираз мантиси.

0	1	2	...	...	...	...	...	...	m+n+1
0	0	1	2	...	m	1	2	...	n

_____ _____ _________________________ __________________________

   

Знак Знак Порядок Мантиса

числа порядку

У комп’ютерах із рухомою комою можливе переповнення розрядної сітки, так само, як і у комп’ютерах із фіксованою комою. Наприклад, переповнення може виникнути при додаванні нормалізованих чисел одного знаку з однаковими порядками. У цьому випадку з’являється “1” ліворуч від коми. Такого роду переповнення коригується зсувом мантиси вправо на один розряд і збільшенням порядку на одиницю, тобто виконується “нормалізація вправо”.