1.3.4. Модифіковані коди

Ці коди відрізняються від простих машинних кодів тим, що на відображення знака відводиться два розряди: плюс відображається двома нулями (00), а мінус - двома одиницями (11). З погляду побудови АЛП вони зручні для виявлення переповнення розрядної сітки, яке може виникнути при додаванні чисел. Значення 01 та 10 у знакових розрядах свідчать про переповнення розрядної сітки.Невизначеність знаку приводить до того, що результат у цьому вмпадку втрачається.

У модифікованих кодах другий розряд ліворуч від коми визначає знак числа, а перший розряд служить для аналізу переповнення розрядної сітки при виконанні арифметичних операцій над числами.

Перетворення двійкових чисел у модифіковані прямий, доповняльний і обернений коди проводиться за правилами, розглянутими вище.

Приклад 1.3.6. Подати двійкові числа А₁= +0,1101101 і А₂= - 0,1101101 у прямому,

доповняльному і оберненому модифікованих кодах.

Перетворення чисел у заданий код у комп'ютерах відбувається автоматично як при вводі чисел у комп’ютер, так і при виконанні операцій.

1.1. Додавання і віднімання двійкових чисел з фіксованою комою

Простота виконання арифметичних дій є важливою особливістю двійкової системи числення. Але у дійсності, при виконанні арифметичних операцій у конкретному комп’ютері потрібно додатково враховувати не тільки знаки чисел, що обробляються, але і діапазон та форму подання чисел.

Відомо, що одним з можливих шляхів виконання операції віднімання є заміна знаку числа, яке віднімається, на протилежний і додавання його до зменшуваного.

А - В = А + ( - В)

Таким чином операцію арифметичного віднімання замінюють операцією алгебраїчного додавання, яку можна виконати за допомогою двійкових суматорів. Нагадаємо, що від’ємні числа у комп’ютері подаються у прямому, доповняльному і оберненому кодах.

Числа зберігаються у прямому коді, перед виконанням обчислень перетворюються у потрібний – доповняльний або обернений - код і після виконання обчислень знову перетворюються у прямий код.

При реалізації заміни віднімання додаванням, другий доданок у наведенному виразі переводиться у доповняльний код шляхом інвертування та додавання одиниці у молодший розряд. (Треба пам’ятати, що доповняльний код додатного числа співпадає з прямим кодом).

A –B = A +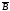+1

При додаванні двох двійкових чисел, за абсолютною величиною менших одиниці, код суми може за абсолютною величиною перевищити одиницю або стати рівним їй. У такому випадку відбудеться переповнення розрядної сітки, що призведе до неправильного результату. У таких випадках результату не існує. Переповнення може відбутися у тих випадках, коли доданки мають однакові знаки. Ознакою переповнення розрядної сітки слугує протилежність знаку суми, що отримана, знакам доданків.

Для отримання коректного резултату при додаванні двійкових чисел з фіксованою комою обов’язковою є умова, щоб кожний з доданків і їх сума за абсолютною величиною були менше одиниці.

1.2. Додавання двійкових чисел у модифікованому доповняльному коді

Доповняльні коди чисел додаються порозрядно. Причому знакові розряди додаються як звичайні розряди цілих чисел. Одиниця переносу, яка виникає при додаванні знакових розрядів, не враховується, тобто відкидається. Суму отримуємо у доповняльному коді. Для отримання остаточного результату цю суму необхідно обов’язково перевести у прямий код, тобто зробити друге доповнення.

Приклад 1. Додати у модифікованому доповняльному коді двійкові числа А і В при наступних умовах:

1. А > 0; B > 0; A + B > 0.

A = + 0,1101; B = + 0,0001 +

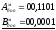
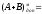00,1110; 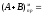00,1110;

2. А < 0; B < 0; A + B < 0.

A = - 0,1101; B = - 0,0001; +

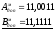
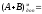111,0010; 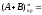11,1110;

Одиниця переносу з старшого знакового 

розряду не враховується

При переведенні у прямий код отриманих від’ємних результатів переводиться саме число і не переводиться знак (див. приклад 4), або число із спотвореним знаком береться за абсолютною величиною.