
- •1.3.1. Прямий код
- •1.3.2. Обернений код
- •1.3.3. Доповняльний код
- •1.3.4. Модифіковані коди
- •1.1. Додавання і віднімання двійкових чисел з фіксованою комою
- •1.2. Додавання двійкових чисел у модифікованому доповняльному коді
- •1.3. Додавання двійкових чисел у модифікованому оберненому коді
- •1.4. Переповнення розрядної сітки при додаванні у модифікованих машинних кодах
- •1.1. Подання чисел з рухомою комою
- •1.2. Додавання (віднімання) двійкових чисел з рухомою комою
1.3.1. Прямий код
Він базується на природньому поданні чисел у вигляді їх абсолютного значення з кодом відповідного знаку: плюса (0) або мінуса (1) у старшому розряді.
Формула утворення прямого коду двійкового числа А = ± 0, а1а2а3…аn має вигляд
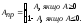 (1.3.1)
(1.3.1)
Приклад 1.3.1. 1. А = + 0,1101; Апр = 0,1101.
2. А = - 0,10101; Апр = 1 - (-0,10101) = 1 + 0,10101 = 1,10101.
Таким чином, цифрові розряди числа у прямому коді залишаються незмінними, а у знаковій частині записується одиниця для від’ємного числа і нуль для додатного числа.
(У цьому прикладі після коду знаку поставлено умовно кому. Насправді, у комп’ютері „фізичної” коми не може бути. Надалі, для того, щоб чітко відрізняти знак від самого числа у прикладах, ми будемо всюди ставити умовну кому).
З (1.3.1) витікає, що нуль в прямому коді може бути додатним і від’ємним:
А= +0,00 … 00; Апр= 0,00 … 00.
А= -0,00 … 00; Апр= 1,00 … 00.
У комп'ютерах інформація зберігається у запам’ятовуючих пристроях (ЗУ), у пристроях вводу і виводу завжди у прямому коді.
1.3.2. Обернений код
Обернений код від’ємного числа називають доповненням до 1. Тут так само присутній знаковий розряд (0 – це “+”, 1 – це “-”).
Формула утворення оберненого коду має вигляд
Аоб
=
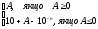
 (1.3.2)
(1.3.2)
Обернений код додатного числа повністю співпадає з відображенням числа у прямому коді
Приклад 1.3.2. А = - 0,100110.
Аоб = 10 + (– 0,100110) – 0,000001 = 1,011001.
Звідси витікає правило: щоб записати від’ємне число в оберненому коді, потрібно у знаковому розряді цього числа поставити одиницю, а в числових розрядах нулі замінити одиницями, а одиниці – нулями. Операція заміни нуля на одиницю і навпаки називається інвертуванням.
В оберненому коді нуль зображається неоднозначно, є два подання нуля: + 0 і – 0.
А = + 0,00 … 00; Аоб = 0,00 … 00;
А = - 0,00 … 00; Аоб = 1,11 … 11;
Така ситуація створює проблему, оскільки бажано мати систему, у якій існує тільки одне зображення любої цифри, у тому числі і нуля.
1.3.3. Доповняльний код
Для подання від’ємних чисел у двійковій системі числення частіше використовується система доповнення до двох. У ній також є знаковий розряд (0 це “ + ”, а 1 – це “-”). Доповнення виконується у два етапи. Спочатку кожна 1 міняється на 0, а кожний 0 – на 1 (інверсія). Потім до молодшого розряду отриманого результату додається 1. Наприклад, розглянемо перетворення вісьмирозрядного числа - 610 у форму з доповненням до двох:
000001102 = (+ 6)10
111110012 = (- 6 у системі з доповненням до 1)
111110102 = (- 6 у системі з доповненням до 2).
Формула утворення доповняльного коду двійкового числа має вигляд
Адоп
=
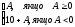 (1.3.3)
(1.3.3)
Приклад 1.3.3. А= - 0,101010; Адоп = 10 + (- 0,101010) = 1,010110.
Як видно з виразу (1.3.3), доповняльний код додатного числа повістю співпадає з зображенням числа у прямому коді.
Порівнюючи від’ємне число А з його доповняльним кодом Адоп, можна вивести наступне правило: щоб записати від’ємне число у доповняльному коді, потрібно у знаковому розряді цього числа поставити одиницю, а у всіх числових розрядах нулі замінити одиницями, а одиниці – нулями і до отриманого результату добавити одиницю до молодшого розряду.
Приклад 1.3.4. Записати двійкове число А = - 0,0101 у доповняльному коді.
А = - 0,010 = Адоп = 1,1010 + 0,0001 = 1,1011.
Щоб перетворити доповняльний код від’ємного числа у прямий код, потрібно у числових розрядах цього числа замінити нулі на одиниці, а одиниці на нулі і додати до отриманого результату одиницю молодшого розряду, тобто, виконати друге доповнення.
Приклад 1.3.5. Перетворити доповняльний код Адоп=1,1011 від’ємного числа у прямий код.
Апр= 1,0100 + 0,0001= 1,0101.
У доповняльному коді від’ємний нуль відсутній. Тому доповняльний код використовується частіше, ніж обернений. Але у цій формі є інша особливість. Набір бітів, що складається з 1, за яким йдуть усі нулі (наприклад, 10, 100, 1000, . . .) є доповненням до самого себе.
