управ.рішення - копия - копия

Оскільки ми домагаємося мінімального значення в, то нас буде цікавити пряма, розташована в найбільшому видаленні вправо від прямої в = 22,8 і минаюча через багатокутник ABCDEF, тобто пряма у_тіп

Єдиною точкою, що відповідає оптимальному плану, буде та вершина багатокутника ABCDEF (див. рис. 2.8), що одночасно належить області допустимих планів і відповідає вимозі мінімі­зації цільової функції в, — вершина С. З рівняння прямої ВР, що проходить через точку 3, випливає, що Xj = 4. З рівняння прямої DC, що проходить через ту ж точку, випливає, що х₂ = 0.

Підставляючи отримані значення х₂ = 4 і х₂ = 0 у рівняння (2.3), визначимо величину іншої перемінної, складової оптималь­ного плану.

Теорія і практика розробки управлінських рішень

При розв'язанні цих завдань цільова функція розрахо­вується за формулою, аналогічною

(2.8)

y=3₁x₁+3₂x₂+...+c_jf+c_nK_n,

де у — цільова функція, що підлягає максимізації. Відмінність полягає в тім, що знаки перед усіма постійними ко­ефіцієнтами міняються "плюс" на "мінус" (с) = -с у.

Приклад 20. (Динамічне програмування). Літак ванта­жопідйомністю G = 83 умовних одиниць вантажу передбачається завантажити чотирма типами вантажу (т - 4) відповідно до да­них, наведених в таблиці 2.11 ?

Таблиця 2.1J Маси і вартості вантажу 1-го типу (в умовних одиницях)

Показник, умовні одиниці	Тип вантажу, і
	1	2	3	4
Рі Сі	10 20	16 50	22 85	24 96

Необхідно завантажити літак таким чином, щоб загальна цінність вантажу була максимальною.

Розв 'язок

У даному прикладі немає природного поділу операції за­вантаження на кроки. Такий поділ, в інтересах розв'язання за­вдання, доцільно ввести штучно, приймаючи за кроки заванта­ження літака предметами різних типів. Таких кроків буде чотири. Послідовність розрахунків при цьому буде наступною. На пер­шому колі оптимізація починається з четвертого типу вантажу — четвертого кроку. При цьому приймається, що літак завантажу­ють тільки предметами 4-го типу. У цих умовах максимальна цінність вантажу на четвертому кроці:

a>₄=f₄(G)=Max{x₄,3₄} (2.9)

при умовах, що випливають з параграфа 13.3 (с. 243),

¹ Джерело те ж (В.А.Абчук)

35*?

В.О. Василенко

356

Теорія і практика розробки управлінських рішень

Для кожного з цих чотирьох значень обчислюється величи­на, що стоїть у фігурних дужках формули (2.10), причому f₄(G) розраховується за формулою (2.9).

Підставивши відповідні цифри і виконавши нескладні арифметичні дії, одержимо наступні значення:

Длях₃ = 0- 288; х₃ = 1 - 277; х₃ = 2- 266 і для х₃ = 3 вели­чину, рівну 255.

Потім розраховується максимальна величина з отриманих значень:

A3) = мах (288; 277; 266; 255) = 288.

Відповідна цій найбільшій цінності кількість вантажу х₃ = 0 і буде умовним оптимальним керуванням на третьому кроці:

U₃=x₃ = 0.

Далі переходимо до попереднього, другого кроку — до за­вантаження предметів другого типу, для якого аналогічним шля­хом знаходимо

fi(G) = 288 і відповідне U₂=x₂ = 0. Точно так само, для пер­шого кроку

f₁(G) = 308\U_l =_Xl = L

Для першого кроку умовне оптимальне керування одночас­но є оптимальним керуванням U_}*:

и_}*=и!=1.

Потім починається друге коло оптимізації від першого кро­ку до останнього кола нашого завдання.

Оскільки нам відомо, що оптимальне керування на першо­му кроці вимагає однієї одиниці вантажу першого типу, то надалі розподіляється тільки те, що залишається на інші типи вантажу, а саме:

G' = 83 - 1 • 10 = 73 одиниці.

Роблячи розрахунки, аналогічні до тих, що виконувалися на першому колі, послідовно одержуємо оптимальні керування для другого, третього і четвертого кроку:

U₂*=0; U₃*=0;U₄*^3.

Оптимальне керування забезпечує наступну максимальну загальну цінність вантажу, що розраховується за формулою на­веденою в теоретичній частиш параграфа 13.3 (с. 243):

W= 1 • 20 + 0* 50 + 0' 85 + 3 * 96 - 308.

У розглянутому прикладі оптимізація могла бути здійсне­на, починаючи з будь-якого типу предметів. Прийнятий нами по­рядок відповідає загальній ідеї динамічного програмування.

357

В.О. Василенко

Приклад 21. Маємо п'ять видів ресурсів (т =5), призначе­них для чотирьох об'єктів (п = 4). Відомі характеристики об'єктів і ресурсів: матеріальний ефект при розподілі на і-й об'єкт будь-якого ресурсу (Аі) і коефіцієнти аі, що характеризують можливос­ті кожного з ресурсів стосовно до конкретних об'єктів (табл. 2.12)4

Таблиця 2.12 Характеристики об'єктів і ресурсів

Характеристики	Номери об'єктів
	1	2	3	4
Аі.	16	14	12	2
аі	ОД	ОД	ОД	ОД

Необхідно визначити кількість ресурсів (х), використання яких на кожнім з об'єктів забезпечить максимальний ефект.

Розв 'язок

У даному прикладі так само, як і в попередньому, немає природного поділу операції на етапи. Такий поділ в інтересах розв'язання завдання вводиться штучно. За кроки приймається послідовний розподіл ресурсів за об'єктами. Таких кроків буде чотири.

На першому колі знаходиться умовне оптимальне керуван­ня — кількість ресурсів, виділених на кожен об'єкт, починаючи з останнього.

На першому кроці позначимо х_г, кількість ресурсів, що на­правляються на останній об'єкт (рахунок кроків ведеться з кінця). При цьому ефективність на останньому кроці

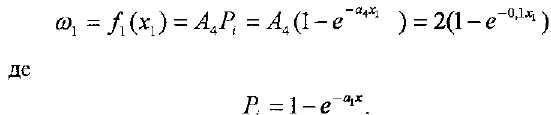
(2.12)

Значення X; нам невідомо, тому що це та кількість ресурсів, що залишилася від умовного оптимального керування на передо­станньому (другому з кінця) кроці.

Теорія і практика розробки управлінських рішень

Переберемо всі можливі значення х_} і для кожного з них зробимо розрахунок f_}(xj за формулою (2.12).

Як видно з умови завдання, х_г може приймати значення 0, 1,2, 3, 4, 5. Для цих значень і зробимо розрахунок (табл. 2.13).

Таблиця 2.13 Можливі значення х, і ефективності

X!	ftfxi)
1	'0,190
2	0,363
3	0.518
4	0,659
5	0.787

На другому кроці (з кінця) виділяється х₂ ресурсів на пере­достанній об'єкт, а відповідна ефективність на цьому кроці со₂ по­винна враховувати, крім ефекту від другого кроку, також і ефект в результаті умовного оптимального керування на першому (з кінця) кроці:

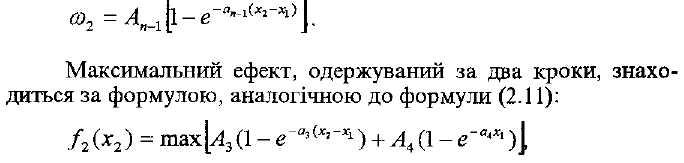
де 0<х₂<х₂

Оскільки х₂ — кількість ресурсів, призначених для забезпе­чення як передостаннього, так і останнього об'єкта, то х₂ > х₂. Ви­ходячи з цього, роблять припущення про всі можливі значення х₂ (х₃ =0, 1, 2, 3, 4, 5) і для кожного з них розраховується ефек­тивність (табл. 2.14).

Одночасно знаходиться і значення х₂ (умовне оптимальне керування), при якому f₂(x₂) досягає максимуму. Оскільки воно залежить від х₂, позначимо його х/х₂) і також приведемо в табли­цю 2.14.

^А Джерело те ж (В.А.Абчук) 358

359

В.О. Василенко

Таблиця 2.14

Можливі значення х₂, максимальні ефективності і відповідні до них значення х₂ (х^

Х2	Ї2(Х2)	Хі(Х2)
0	0	0
1	1.150	0
2	2,175	0
3	3.108	0
4	3.954	0
5	4.722	0

Далі аналогічним шляхом для всіх можливих значень х₃ об­числюються /₃(хз) і х₂(х₃), наведених у таблиці. 2.15.

У такий же спосіб розраховується й умовне оптимальне ке­рування на четвертому (з кінця) кроці. Але оскільки на цьому кроці ми підійшли до вихідного (початкового) значення кількості одиниць ресурсів, призначених для всіх об'єктів (т = 5), то вели­чина х₃ визначається тільки для х₄ = 5. Як показує розрахунок, х₃(х₄ = 5) =2.

Таблиця 2.15

Можливі значення х₃, максимальні ефективності/₃(хз) і відповідні до них значення х₂(х₃)

Хз	F3(x3)	Х2(Хз)
0	0	0
1	1,330	0
2	2;541	0
3	3,508	2
4	4,680	2
5	5.804	2

Починається друге коло оптимізації в зворотному порядку (від четвертого кроку до першого). Оскільки спочатку в нас для всіх об'єктів є 5 од.р., а після виділення ресурсів на один з об'єктів відповідно до умовного оптимального керування на всі інші повинно залишитися х₃(х₄) = 2 одиниць ресурсів, то опти­мальне керування на четвертому (з кінця) кроці

U4* = х₄ = 5 ~ 2 = З одиниці.

360

Теорія і практика розробки управлінських рішень

Оптимальне керування на третьому (з кінця) кроці повинно бути таким, щоб при розподілі 5 - 2 =3 одиниці ресурсів, що за­лишилися, дотримувався принцип оптимальності. Як ми вже знаємо, при цьому х₃* = x₃(xj = 2.

Як показує аналіз таблиць 2.13, 2.14 і 2.15, при х₃ = 2 х₂{х₃) = 0, при х₂ = 0х₁(х₂) = 0. Отже, х₂* = Xj* = 0.

Отже, оптимальним цільовим розподілом одиниць ресурсів (од. рес.) за об'єктами буде:

U4* - 3 ед. p., U3* = 2 ед.р., U2* = 0ед.р., Ul* = 0 ед.р. Загальний збиток при цьому

Приклад 22. (Стохастичне програмування). Розглянемо за­вдання розподілу двох видів ресурсів для випуску двох наймену­вань виробів [13].

Математична постановка завдання має вигляд:

361

В.О. Василенко

Вихідні, дані, необхідні для розв'язання цього завдання, наве­дені в табл. 2.16, 2.17.

D

Таблиця 2.16 Вихідні параметри завдання

d

Параметри

XI

362

Таблиця 2.17 Необхідні обмеження й умови

Обмеження	Випадкові відхилення
	аи		а?.		Ьі
	an	Щіі	а а	°п	bi
1 2	10 20	2 6	15 14	3 4	100 150	9 12

Теорія і практика розробки управлінських рішень

Таблиця 2.18 Результати детермінованого розв 'язання

Параметр	^і-0	а, = 0,6
Х\	2,0	2
Х2	5.3	5,04
L	52,4	50,3
Р	0	4,0
Si	0	4,4
ь	0	5,8
Yi	0	4,4
Y2	0	5,1

Розглянемо тепер, як вплинуть на результат розв'язання за­вдання величини, що визначають її ймовірний характер. До та­ких величин відносять: заданий рівень ймовірності а_і і дисперсії <?,-, і &і. Почнемо з аналізу впливу а₁₂ (табл. 2.19).

Таблиця 2.19 Таблиця аналізу впливу випадкових факторів

	«і і
	0,5	0,6	0,77	0,89	0,96	0,987
X:	2,0	2,0	2,0	3,7!	3,07	2J65
х2	5,3	5,04	4,51	3.0	3,0	3,0
1	52,4	50,3	46,1	42,6	39,3	34,8
Р	0	4,0	12,0	18,7	25,0	33,6
	0	4,4	12,3	17,9	24,3	33,3
	0	5,1	14,8	16,5	23,2	26,0

З аналізу розв'язання цього завдання можна зробити наступні висновки: для забезпечення гарантованого (з ймовірністю а = 0,6) виконання плану необхідно мати додатково близько 5% кож­ного виду ресурсу. При відсутності додаткового ресурсу цільова функція може зменшитися на величину р = 4% внаслідок можли­вого скорочення випуску продукції х₂ від 5,3 до 5,04.

Приклад 23. (Теорія ігор). Підприємець володіє трьома видами товарів Л_ь А₂, А_І7, які він прагне реалізувати на ринку, де можливий продаж конкурентом аналогічних товарів — У_ь В₂ і В_3і відповідно.⁵

^; За основу взято завдання, наведена в джерелі В.А. Абчук. Економіко-математичні методи. Елементарна математика і логіка. Методи дослід­ження операцій. - СПб: Союз,1999. — 370 с.

363

В.О. Василенко

Підприємцю невідомо, який вид товарів переважно конку­рент буде продавати на ринку, а конкуренту невідомо, які товари підприємця на цьому ринку з'являться.

Підприємець має у своєму розпорядженні дані про те, яка ймовірність продати той чи інший товар при наявності на ринку товарів конкурента. Ці дані утворять матрицю гри (табл. 2.20).

Необхідно дати підприємцю рекомендації з раціонального вибору виду товарів для просування їх на ринок в умовах конку­ренції, при якому забезпечується одержання можливого найкра­щого результату — найбільшої ймовірності продажів, що б не починав конкурент.

Розв 'язок

Виписуємо праворуч мінімуми рядків і з них вибираємо найбільший <з₂= 0,4 (відзначений зірочкою). Це нижня ціна гри, чи максимін. Потім виписуємо внизу максимуми стовпців і з них вибираємо найменший (fa = 0,8) — відзначений зірочкою. Це верхня ціна гри, чи мінімакс.

Таблиця 2.20 Матриця гри

Підприємець	Конкурент
	Ві	в2	Вз	ГЇ.1
Аі	0,0	0.4	0.9	0.4
А2	0.2	0.9	0.1	0.1
А.	0.8	0.0	1.0	0.0
0*	0,8	0,9	1,0

Розв'язання полягає в тім, що необхідно систематично за­стосовувати Максимівну стратегію — товар типу A_h При цьому підприємцю гарантується результат не менш/> = 0,4, що б не по­чинав конкурент (його задуми нам не відомі). Для конкурента найкраща стратегія — вибір товару виду В₂; при цьому він гаран­тує собі результат не більш р = 0,8 (чим прибуток підприємця більше, тим для нього гірше).

Оскільки в розглянутому прикладі немає сідлової точки (а Ф fy, це означає, що отримані рекомендації вірні лише для ви­падку, коли конкурент не має у своєму розпорядженні даних про обране підприємцем рішення. Це так звана хитка стратегія. Якщо конкурент довідається про те, що підприємець став застосовува­ти товар типу А₂ він відразу ж почне застосовувати товар виду В₃ і тим самим поліпшить свій результат до р = ОД. 364

Теорія і практика розробки управлінських рішень

У тих випадках, коли в подібному завданні конкурент має у своєму розпорядженні дані про вибір підприємця, необхідно шу­кати розв'язання в змішаних стратегіях.

Приклад 24. В умовах прикладу 23. підприємцю стали відомі можливі кількості одиниць кожного з його товарів, що можуть бути продані при різних варіантах появи товарів конкурента на ринку (табл. 2.21).

Необхідно дати підприємцю рекомендації, при викорис­танні яких середньоочікувана кількість проданих товарів буде найбільшою, що б не починав конкурент.

Таблиця 2.21 Матриця гри

Підприємець	Конкурент
	в,	в2	В3	а.
А, А2 А,	5 8 9	6 7	8 7 6	5 7* 6
ft	9	f ""	8