Теоретичні розподіл часу напрацювання до відмови

У зв'язку з тим, що на процеси виготовлення електронних засобів та їх експлуатацію постійно діє чимало дестабілізуючих факторів, повні характеристики їх надійності дуже розкидані. Значення цих характеристик є випадковими величинами, і для їх аналізу в якості моделі часто використовують відомі з теорії ймовірності неперервні розподіли. До них належать:

- показовий розподіл;

- нормальний або гауссовий розподіл;

- рівноімовірний розподіл;

- розподіл Релей;

- розподіл Ерланга;

- розподіл Вейбулла;

- логарифмічно нормальний;

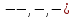розподіли, розподіл Стьюдента, ² та інші.

Розглянемо деякі з них.

Показовий (експоненціальний) розподіл часу напрацювання до відмови спостерігається тоді, коли відносна швидкість зменшення ймовірності безвідмовної роботи зі збільшенням часу роботи є постійною величиною, тобто

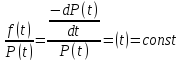
Експоненціальний закон розподілу використовується частіше ніж інші закони при дослідженні надійності елементів і систем Це пояснюється рядом причин, головними з яких є наступні:

По-перше, показовий розподіл часу напрацювання до відмови часто підтверджується на практиці. Цей розподіл є типовим для складних систем, в які входять різнорідні елементи з різними: -характеристиками. Інтенсивність відмов таких систем може бути практично постійною при суттєво нестаціонарному характері інтенсивності відмов окремих елементів. В період нормальної експлуатації, до початку періоду зношення, інтенсивність можна вважати незмінною.

По-друге, при стаціонарному характері інтенсивності відмов елементів отримують доволі прості формули для розрахунку надійності. Важливість спрощення розрахунків надійності має особливе значення для складних систем з десятків і сотень тисяч елементів.

По-третє, дослідження надійності часто проводиться при обмеженій інформації про відмови виробів у процесі експлуатації або у процесі випробувань. При цьому виявити суттєві відхилення від гіпотези про стаціонарний характер - характеристики стає просто неможливо. Природно, що в цих умовах як перше наближення приймається закон розподілу, який найчастіше зустрічається на практиці, тобто показовий закон.

При показовому розподілі часу напрацювання до відмови густина розподілу описується формулою:

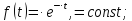
Ймовірність безвідмовної роботи (функція надійності):

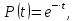
а ймовірність безвідмовної роботи системи з 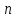- eлeмeнтів:

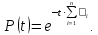
Математичне сподівання часу напрацювання до відмови, його дисперсія визначаються за формулами:

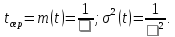
Підкреслимо, що показовий розподіл часу напрацювання пристроїв до відмови найкраще використовувати тоді, коли можна знехтувати впливом припрацювання, зношення та старіння.

Нормальний закон розподілу. Загальний нормальний розподіл неперервної випадкової величини 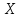характеризується тим, що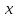може при цьому приймати будь-які значення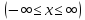. Його густина розподілу має вигляд:

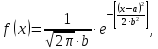
де 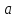, 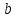– постійні величини, які називаються параметрами нормального закону розподілу випадкової величини.

Основними числовими характеристиками нормального закону розподілу є наступні:

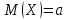–математичне очікування;

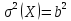–дисперсія;

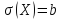–середнє квадратичне відхилення;

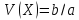–коефіцієнт варіації.

Нормальний закон розподілу використовується тоді, коли випадкова величина х залежить від великої кількості випадкових факторів, однорідних за своїм впливом.

Загальний нормальний закон використовується при оцінці надійності виробів в процесі їх зносу і природного старіння, його застосовують для визначення часу напрацювання до відмови і т.п. Нормальний закон називається граничним через те, що до нього наближаються інші закони розподілу при типових умовах, що часто зустрічаються.

В якості неперервної випадкової величини виступає час напрацювання до відмови. Оскільки час напрацювання до відмови є величиною тільки додатною, тому його розподіл може бути тільки обмеженим.

У зв'язку з великим теоретичним і прикладним значенням нормального розподілу його часто використовують і при явно несиметричному розподілі часу напрацювання до відмови. Для цього підбирають деяку функцію випадкового напрацювання до відмови, наприклад, 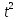, 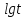та інші.

Закон розподілу Релея є асиметричним законом розподілу часу напрацювання до відмови (рис.6). Він описується функцією виду

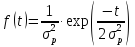
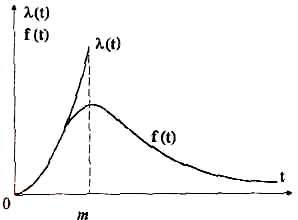
Його функція надійності має вигляд

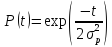
Інтенсивність відмов

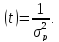
У цих залежностях 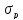– параметр розподілу Релея.

Для розподілу Релея математичне сподівання і середнє квадратичне відхилення часу напрацювання до відмови визначається за формулами:

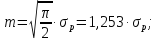
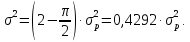
Логарифмічно-нормальний закон є також асиметричним законом розподілу часу напрацювання до відмови.

Розподіл випадкової величини 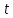називаєтьсялогарифмічно-нормальним, якщо логарифм цієї величини розподіляється за нормальним законом, тобто

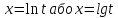
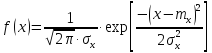
де 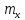і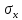- параметри розподілу величини.

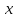Логарифмічно-нормальний розподіл використовується при оцінці відмов за рахунок зношення. В тих випадках, коли відмова виникає через пошкодження за рахунок втомленості, напрацювання до відмови підпорядковується логарифмічно-нормальному розподілу. Цей закон застосовується також для оцінки витрат часу, необхідного для пошуку та усунення несправностей.

Розподіл Вейбула часто використовується для дослідження надійності електронних пристроїв на стадіях їх виготовлення і експлуатації, зокрема, для математичного опису зміни в часі інтенсивності відмов ( - характеристик).

Густина розподілу Вейбула описується формулою:

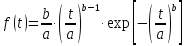
, – параметри розподілу Вейбула, постійні додатні числа. Для кожного класу виробів вони мають визначені значення.