
- •Основи точності та надійності електронних апаратів частина і. Основи теорії надійності електронних засобів
- •Елементи теорії ймовірності
- •Показники надійності
- •Теоретичні розподіл часу напрацювання до відмови
- •Надійність типових елементів
- •Методи розрахунку надійності
- •Орієнтовні методи розрахунку надійності
- •Уточнений або повний розрахунок надійності
- •Показники довговічності
- •Показники відновлюваності (ремонтопридатності)
- •Комплексний показник надійності
- •Методи забезпечення надійності
- •Конструкторсько-технологічні методи підвищення надійності
- •Класифікація способів резервування
- •Класифікаційна таблиця способів резервування
- •Аналіз надійності системи з загальним постійним резервом
- •Аналіз надійності системи з постійним роздільним резервуванням
- •Частина іі. Основи точності та стабільності функціонування еа
- •Методи аналізу точності функціональних вузлів
- •Імовірнісний метод аналізу точності
- •Експериментальні методи дослідження конструкцій та технологічних процесів
- •Планування експериментів
Елементи теорії ймовірності
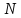 - кількість
дослідів;
- кількість
дослідів;
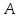 - подія;
- подія;
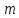 - кількість
появ події
- кількість
появ події
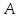 в
в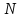 дослідах.
дослідах.
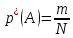
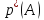 -
статистична подія. При
-
статистична подія. При
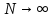 буде наближатись до теоретичної.
буде наближатись до теоретичної.
Сумою кількох випадкових подій називається така подія, яка полягає у здійсненні хоча б однієї з подій, що додаються (сума сумісних І - АБО).
Якщо дві і більше подій не можуть відбутися одночасно, вони називаються несумісними. Якщо дві і більше подій можуть відбутися одночасно, вони називаються сумісними (операція АБО для несумісних подій).
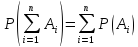
- ймовірність подій дорівнює сумі ймовірностей цих подій (для несумісних подій).
Добутком подій називається така подія, яка полягає в одночасному здійсненні всіх подій (логічна операція І).
Безвідмовна робота системи складається з безвідмовної роботи кожного з елементів.
При паралельному з'єднанні розглядаємо відмову системи.
Сума двох протилежних подій дорівнює 1.
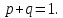
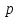 -
безвідмовна робота;
-
безвідмовна робота;
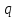 -
відмова.
-
відмова.
Дві події вважаються незалежними, якщо ймовірність здійснення однієї з них не залежить від того, відбулась друга подія чи ні.
Приклад.
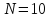 - загальна кількість виробів;
- загальна кількість виробів;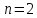 - кількість бракованих виробів.
- кількість бракованих виробів.
1)
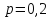 - ймовірність того, що вибраний навмання
виріб буде бракованим.
- ймовірність того, що вибраний навмання
виріб буде бракованим.
2) якщо в першому випадку вибрали бракований виріб, то ймовірність вибрати бракований виріб в другий раз тепер становить 1/9, але, якщо в першому випадку був якісний виріб, то ймовірність браку буде становити 2/9.
Приймаємо припущення, що при послідовному з'єднанні безвідмовна робота елементів (або відмови елементів) - це незалежні випадкові події. Це стосується і паралельних з'єднань.
Ймовірність добутку незалежних випадкових подій дорівнює добутку ймовірностей цих подій:
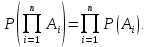
Задача 1. Пристрій складається з двох блоків, з'єднаних послідовно. З метою підвищення надійності кожен з цих блоків дублюється аналогічним через комутатор K. Якщо відмовляє блок А, то спрацьовує комутатор і замість блоку А підключається блок С. Аналогічно, при відмові блоку В спрацьовує комутотатор і підключається блок D.
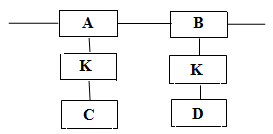
Ймовірність
безвідмовної роботи:
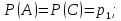
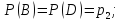
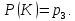
Знайти ймовірність безвідмовної роботи пристрою Р(П) в цілому.
Розв'язування.
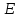 - подія,
яка полягає в безвідмовній роботі
пристрою в цілому. Необхідно сформулювати
структуру події
- подія,
яка полягає в безвідмовній роботі
пристрою в цілому. Необхідно сформулювати
структуру події
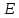 .
.
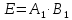 -
безвідмовно працюватимуть блоки
-
безвідмовно працюватимуть блоки
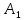 і
і
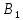 .
.
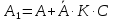 ,
,
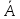 --
протилежна подія (блок
--
протилежна подія (блок
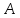 відмовив).
відмовив).
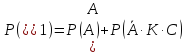 - сума
несумісних подій.
- сума
несумісних подій.
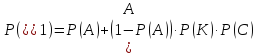
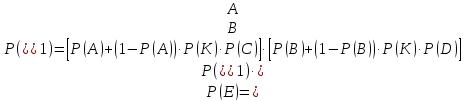
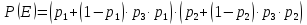
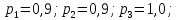
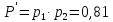 -
Ймовірність
безвідмовної роботи системи без
дублювання.
-
Ймовірність
безвідмовної роботи системи без
дублювання.
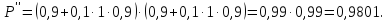
Як бачимо, дублювання дає суттєве зростання ймовірності безвідмовної роботи системи.
Задача 2.
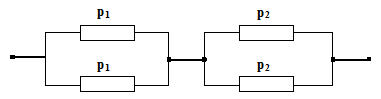
Переходимо до ймовірності відмов при паралельному з'єднанні (обов'язково). Тоді ймовірність відмов цього з'єднання буде дорівнювати добутку ймовірностей
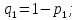
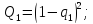
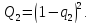
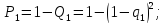
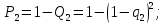
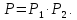
Задача 3.
|
|
|
Показники надійності
Показником надійності називають кількісну міру наявності у виробі тієї чи іншої властивості надійності. Показники надійності діляться на 4 групи:
- показники безвідмовності;
- показники довговічності;
- показники ремонтоздатності (відновлюваності);
- показники збереженості.
Крім того, є декілька комплексних показників, які враховують одночасно 2 чи більше властивостей.
Показники безвідмовності (5 найбільш важливих).
Ймовірність безвідмовної роботи (ймовірність відмови).
Частота відмов.
Інтенсивність відмов.
Середній час безвідмовної роботи.
Напрацювання на відмову.
Оскільки раптові відмови - випадкові події, а час роботи до відмови випадкова величина, то всі показники безвідмовності є певними категорією теорій ймовірності, а на практиці це об'єкти математичної статистики.
Ймовірність безвідмовної роботи – це ймовірність того, що вироби даного типу збережуть працездатність протягом певного проміжку часу у визначених умовах експлуатації.
Задача.
Формується група з
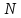 однотипних виробів. Вони випробовуються
протягом деякого неперевного проміжку
часу
однотипних виробів. Вони випробовуються
протягом деякого неперевного проміжку
часу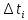 в відповідних експлуатаційних умовах.
В кінці даного проміжку часу підраховується
кількість виробів
в відповідних експлуатаційних умовах.
В кінці даного проміжку часу підраховується
кількість виробів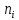 ,
що відмовили.
,
що відмовили.
В цьому випадку ймовірність безвідмовної роботи визначається як число виробів, які відпрацювали безвідмовно, поділене на загальну кількість виробів, поставлених на випробування:
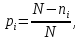
ймовірність відмови:
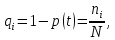
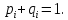
де
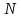 - повинно бути достатньо великим
- повинно бути достатньо великим
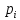 –оцінка
ймовірності (з нормальних великих
чисел)..
–оцінка
ймовірності (з нормальних великих
чисел)..
Ймовірність безвідмовної роботи є функцією часу. За більший проміжок часу відмовить більша кількість виробів, тобто буде більша ймовірність відмов.
Залежність ймовірності безвідмовної роботи від часу:
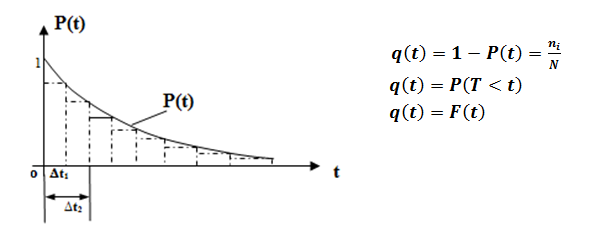
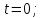
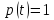
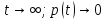
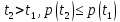
Щоб
достовірно оцінити ймовірність відмов
теоретично:
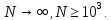
Такий спосіб визначення ймовірності безвідмовної роботи може використовуватись для оцінки безвідмовності компонентів елементної бази.
Задаємо
проміжок часу
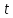 і хочемо визначити ймовірність
безвідмовної роботи. Якщо виріб пропрацює
від 0 до
і хочемо визначити ймовірність
безвідмовної роботи. Якщо виріб пропрацює
від 0 до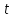 без
відмови, то можна сказати, що відмова
наступить при в момент часу
без
відмови, то можна сказати, що відмова
наступить при в момент часу
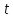 і виріб пропрацює проміжок часу
заданому.
і виріб пропрацює проміжок часу
заданому.
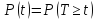
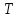 –випадкова
величина часу безвідмовної роботи;
–випадкова
величина часу безвідмовної роботи;
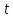 –конкретне
значення часу.
–конкретне
значення часу.
Ймовірність безвідмовної роботи є ймовірність того, що час безвідмовної роботи (як випадкова величина)є не менше від заданого проміжку часу неперервної роботи.
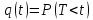
Густина розподілу можлива лише для неперервних випадкових величин. Універсальною формулою закону розподілу є:
Функція закону розподілу - це ймовірність того, що випадкова величина прийме значення менше від заданого
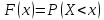
Отже, ймовірність відмови - це функція розподілу часу безвідмовної роботи.
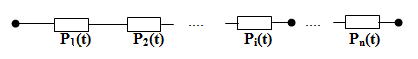
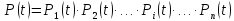
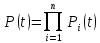
Дана формула є дуже незручною для практичного використання, тому що при великій кількості елементів добуток ймовірностей стає занадто громіздким, особливо якщо мати на увазі, що кожна ймовірність - це величина з декількома 9 - ми після коми. І це основний недолік ймовірності безвідмовної роботи як показника.
Ймовірність безвідмовної роботи нормується для визначеного часу неперервної роботи.
1) Безвідмовність системи завжди менше, ніж безвідмовність будь - якого елемента в даній системі.
2) Зі збільшенням складності виробів безвідмовність падає (збільшується кількість елементів). Із зростанням безвідмовної роботи крива стає більш пологою.
Таким чином, характеристикою може бути похідна від функції розподілу часу
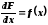 - густина
розподілу.
- густина
розподілу.
Безвідмовність виробу можна характеризувати не лише ймовірністю безвідмовної роботи, а й швидкістю зміни ймовірності в часі (це похідна від ймовірності).
Частота відмов – це середня відносна кількість відмов виробів даного типу за одиницю часу.
Формується
вибірка з
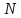 однотипних елементів. Вони випробовуються
протягом
однотипних елементів. Вони випробовуються
протягом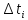 і підраховується кількість відмов за
даний
і підраховується кількість відмов за
даний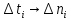 :
:
Відносна кількість відмов за одиницю часу
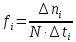
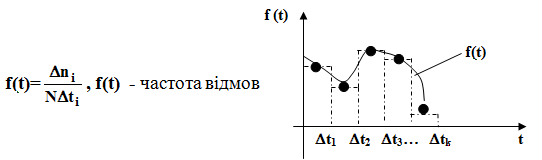
Зв'язок між ймовірністю безвідмовної роботи і частотою відмов:
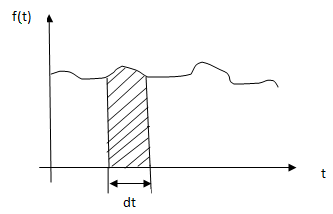
Проміжок
часу
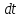 повинен бути настільки малим, що в ньому
може відбутися лише одна відмова.
Ймовірність здійснення однієї відмови
в цьому проміжку набагато більша, ніж
ймовірність здійснення 2-х або більше
відмов.
повинен бути настільки малим, що в ньому
може відбутися лише одна відмова.
Ймовірність здійснення однієї відмови
в цьому проміжку набагато більша, ніж
ймовірність здійснення 2-х або більше
відмов.
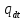 –ймовірність
відмови (чим більше проміжок
–ймовірність
відмови (чим більше проміжок
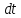 ,
тим більша ймовірність відмови).
,
тим більша ймовірність відмови).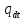 залежить від того, наскільки часто
відбуваються відмови.
залежить від того, наскільки часто
відбуваються відмови.
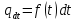
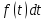 -
ймовірність випадкової події –
ймовірність одного значення неперервної
випадкової величини, якщо
-
ймовірність випадкової події –
ймовірність одного значення неперервної
випадкової величини, якщо
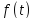 – густина розподілу
– густина розподілу
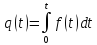
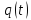 –функція
розподілу часу безвідмовної роботи;
–функція
розподілу часу безвідмовної роботи;
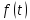 –густина
розподілу часу безвідмовної роботи;
–густина
розподілу часу безвідмовної роботи;
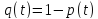 ,
тоді
,
тоді
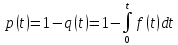
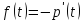 –зв'язок
між ймовірністю безвідмовної роботи
та частотою відмов.
–зв'язок
між ймовірністю безвідмовної роботи
та частотою відмов.
Частота відмов - густина розподілу часу безвідмовної роботи.
Приклад.
Частота відмов описується функцією
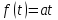 .
Необхідно визначити ймовірність відмови
.
Необхідно визначити ймовірність відмови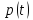 - ?
- ?
Ймовірність відмови:
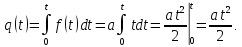
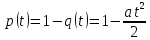
або
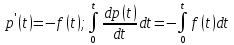
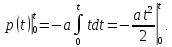
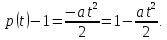
Частота відмов, з теоретичної точки зору, досить важлива характеристика. Але з практичної точки зору частота відмов має один суттєвий недолік:
Оскільки
в процесі випробувань вироби не
відновлюються і не замінюються новими,
то число виробів, які знаходяться на
випробуванні з кожним проміжком часу
зменшується. Оскільки при розрахунку
ми вважаємо об’єм вибірки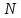 постійним, то отримане значення частоти
відмови будезаниженим.
постійним, то отримане значення частоти
відмови будезаниженим.
3). Для практичного застосування частоту відмов необхідно модифікувати так, щоб враховувати кількість виробів, яка відмовляє в процесі випробовування – модифікована частота відмов називається інтенсивністю відмов.
Інтенсивність відмов – відносна кількість відмов виробів даного типу за одиницю часу при умові, що враховуються вироби, що працюють на початку кожного проміжку часу.
На
початок
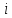 - го проміжку часу відмовило
- го проміжку часу відмовило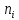 елементів,
які представляють собою накопичену
суму відмов за усі попередні проміжки
часу:
елементів,
які представляють собою накопичену
суму відмов за усі попередні проміжки
часу:
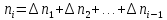
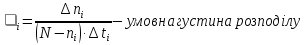
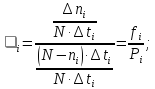
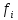 –частота
відмов;
–частота
відмов;
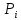 – ймовірність безвідмовної роботи.
– ймовірність безвідмовної роботи.
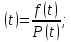
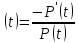
де
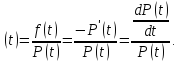
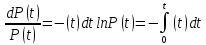
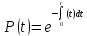
Інтенсивність відмов – це основна характеристика безвідмовності компонентів елементної бази. Саме інтенсивність відмов фігурує як основа для розрахунку рівня безвідмовності. Значення інтенсивності відмов всіх існуючих елементів наведені в довідниках та в галузевих стандартах з надійності.
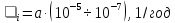
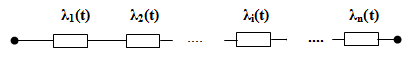
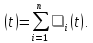
Інтенсивність відмови системи завжди більша від інтенсивності відмов окремого елемента.
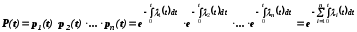

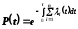
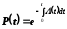 - для
системи.
- для
системи.
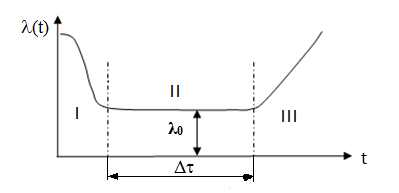
Для всіх
виробів
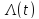 має характерну залежність, яка називаєтьсялямбда-характеристикою:
має характерну залежність, яка називаєтьсялямбда-характеристикою:
І -
період припрацювання виробів
характерний великим
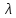 .
Причина появи цього періоду полягає в
тому, що до складу виробів даного типу
при їх виготовленні можуть потрапити
елементи з прихованими дефектами, які
починають відмовляти і збільшується
кількість відмов. По мірі заміни їх
якісними
.
Причина появи цього періоду полягає в
тому, що до складу виробів даного типу
при їх виготовленні можуть потрапити
елементи з прихованими дефектами, які
починають відмовляти і збільшується
кількість відмов. По мірі заміни їх
якісними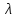 зменшується. Період в межах від одиниць
до сотень годин. До закінчення припрацювання
виріб не повинен потрапити до експлуатації.
Для того, щоб не допустити в експлуатацію
елементи з дефектами на підприємствах
– виробниках в виробничий процес
включають електротермотренування.
Задача електротермотренування –
провести припрацювання елементів.
зменшується. Період в межах від одиниць
до сотень годин. До закінчення припрацювання
виріб не повинен потрапити до експлуатації.
Для того, щоб не допустити в експлуатацію
елементи з дефектами на підприємствах
– виробниках в виробничий процес
включають електротермотренування.
Задача електротермотренування –
провести припрацювання елементів.
ІІ
- період нормальної експлуатації.
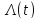 -
практично постійне, відбуваються лише
раптові відміни,
-
практично постійне, відбуваються лише
раптові відміни,
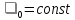 ,
,
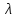 - є
- є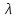 раптових відмов. Тривалість 103÷
104
годин.
раптових відмов. Тривалість 103÷
104
годин.
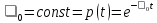
Для періоду нормальної експлуатації час безвідмовної роботи має експоціальний розподіл.
Для ЕРЕ
існують таблиці
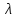 .
Ця інформація використовується для
визначення безвідмовності виробу.
.
Ця інформація використовується для
визначення безвідмовності виробу.
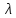 елементів
залежить від умов експлуатації. Тому,
крім поширених значень
елементів
залежить від умов експлуатації. Тому,
крім поширених значень
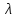 ,
в довідниках чи галузевих стандартах
наведені графічні або табличні залежності
інтенсивних відмов від найсуттєвіших
експлуатаційних факторів.
,
в довідниках чи галузевих стандартах
наведені графічні або табличні залежності
інтенсивних відмов від найсуттєвіших
експлуатаційних факторів.
Стандартно
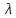 визначається у відсотках за 1000 год:
визначається у відсотках за 1000 год: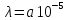 1/год.
1/год.
В сучасних
таблицях
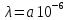 1/год
або
1/год
або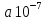 1/год.
1/год.
Нормуючи
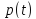 необхідно його супроводити часом
безперервної роботи.
необхідно його супроводити часом
безперервної роботи.
Для продовження періоду нормальної експлуатації проводяться профілактичні заходи, що дозволяє відсунути час інтенсивного зношення і старіння елементів.
ІІІ
- період старіння.
Характеризується різким зростанням
значення інтенсивності відмов
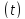 ,
при цьму переважають відмови поступові,
які викликані зносом і старінням. З
початком ІІІ періоду подальша експлуатація
виробу є недоцільною.
,
при цьму переважають відмови поступові,
які викликані зносом і старінням. З
початком ІІІ періоду подальша експлуатація
виробу є недоцільною.
Середній час безвідмовної роботи - час, який вироби даного типу в середньому працюють до першої відмови.
Формується
група з
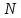 однотипних виробів, які ставляться на
випробовування в початковий момент
часу
однотипних виробів, які ставляться на
випробовування в початковий момент
часу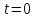 .
В процесі випробовувань здійснюється
постійне спостереження за станом виробів
і фіксуються точні моменти відмов
кожного виробу. Після відмови вироби
знімаються з випробувань.
.
В процесі випробовувань здійснюється
постійне спостереження за станом виробів
і фіксуються точні моменти відмов
кожного виробу. Після відмови вироби
знімаються з випробувань.

Середній
час безвідмовної роботи виробів
- це середнє арифметичне моментів часу
відмов,
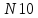 .
.
Математичне очікування часу безвідмовної роботи:
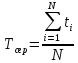
Середнє арифметичне моментів часу отримане експериментальним шляхом, тому представляє собою оцінку математичного сподівання даної величини.
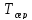 -
математичне сподівання часу безвідмовної
роботи
-
математичне сподівання часу безвідмовної
роботи
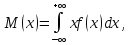
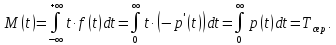
Для
нормальної експлуатації
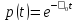 ,
тоді
,
тоді
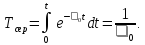
Якщо
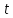 безперервної роботи дорівнює
безперервної роботи дорівнює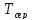 ,
то
,
то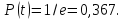
Недолік
показника
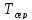 :
велике число виробів, яке необхідно
поставити на випробування.
:
велике число виробів, яке необхідно
поставити на випробування.
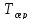 може
бути використане для характеристики
безвідмовності як відновлюваних, так
і невідновлюваних виробів.
може
бути використане для характеристики
безвідмовності як відновлюваних, так
і невідновлюваних виробів.
Тому для характеристики безвідмовності відновлюваних виробів вводиться показник - напрацювання не відмову.
Напрацювання на відмову - застосовується для характеристики безвідмовності відновлюваних виробів.
Напрацювання на відмову - середній час роботи виробів даного типу між двома сусідніми послідовними відмовами. Тобто - це середній час роботи виробу, який припадає на одну відмову.
Вибираємо один виріб даного типу, який ставиться на випробовування в необхідному режимі. За станом цього виробу ведеться неперервне спостереження з точною фіксацією моменту відмови.
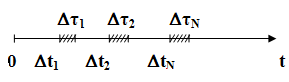
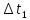 - виріб
відмовив і повертається на випробовування.
- виріб
відмовив і повертається на випробовування.
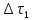 - час
відновлення виробу.
- час
відновлення виробу.
Відновлення виробу означає, що цей виріб після відновлення повністю відповідає всім статичним параметрам, тобто виріб до відмови і після має однакові параметри і характеристики. Це можливо, якщо дана процедура відбувається в період нормальної експлуатації, коли безвідмовність є постійною.
Недолік
напрацювання на відмову
- вимагає досить тривалого часу
випробовувань (доки не наберемо
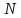 відмов).
відмов).
Напрацювання
на відмову
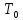 представляє собою середнє арифметичне
часу напрацювання між двома сусідніми
відмовами:
представляє собою середнє арифметичне
часу напрацювання між двома сусідніми
відмовами:
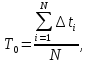
де
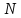 - кількість відмов в процесі випробовування,
- кількість відмов в процесі випробовування,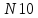 .
.
Для
періоду нормальної експлуатації
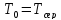 .
.
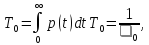
де
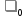 - інтенсивність
відмов - середнє число відмов за одиницю
часу.
- інтенсивність
відмов - середнє число відмов за одиницю
часу.
Ймовірність безвідмовної роботи:
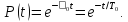
При
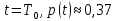 -
середня точка, тобто 37 виробів із 100
відпрацюють нормально, а решта - відмовить.
-
середня точка, тобто 37 виробів із 100
відпрацюють нормально, а решта - відмовить.
На попередній лекції було виведено співвідношення, яке являється основним виразом зв’язку між показниками надійності
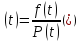
Зміну
у часі показників надійності
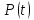 ,
,
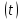 ,
,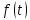 можна зобразити наступним чином
можна зобразити наступним чином
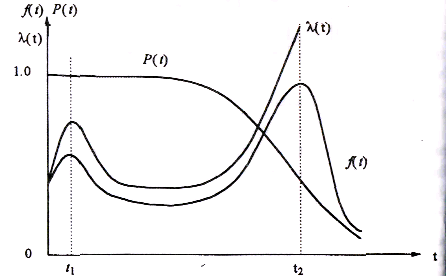
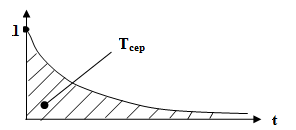
Рис.
1. Зміна у часі показників надійності
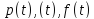
З рисунку
видно, що у початковому періоді
експлуатації, коли
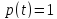 ,
частота відмов
,
частота відмов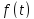 і інтенсивність відмов
і інтенсивність відмов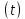 збігаються. При
збігаються. При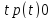 .
.
Точки
перегину
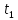 та
та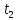 визначають час нормальної експлуатації
виробу.
визначають час нормальної експлуатації
виробу.
Не
зважаючи на важливість співвідношення
(*), воно на практиці використовується
мало. Це пов’язано зі труднощами
експериментального визначення функції
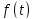 .
Враховуючи
те, що ймовірність безвідмовної роботи
є функцією густини розподілу відмов,
стає можливим вилучити з виразу (*)
функцію
.
Враховуючи
те, що ймовірність безвідмовної роботи
є функцією густини розподілу відмов,
стає можливим вилучити з виразу (*)
функцію
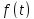 .
Для цього скористаємося виразом:
.
Для цього скористаємося виразом:
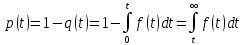
або
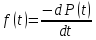
Після
підстановки виразу для
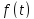 отримаємо
отримаємо
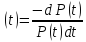
або
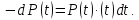
Рішення цього диференціального рівняння має вигляд
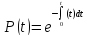
або
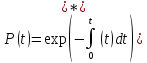
Це
співвідношення є правильним для
будь-якого закону зміни інтенсивності
відмов
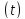 .
В
окремому випадку, коли при
.
В
окремому випадку, коли при
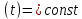 ,
формула (**) набирає вигляду:
,
формула (**) набирає вигляду:
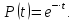
Ця формула часто використовується при розрахунку надійності виробів.

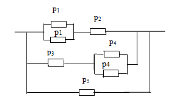
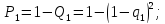
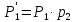 -
ймовірність
безвідмовної роботи першої ланки.
-
ймовірність
безвідмовної роботи першої ланки.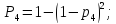
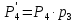 -
ймовірність
безвідмовної роботи другої ланки.
-
ймовірність
безвідмовної роботи другої ланки.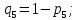
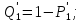
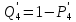 ;
;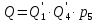 -
ймовірність відмови системи при
паралельному з'єднанні.
-
ймовірність відмови системи при
паралельному з'єднанні. 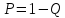 -
ймовірність безвідмовної роботи
системи.
-
ймовірність безвідмовної роботи
системи.