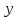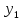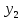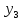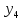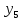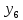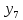Планування експериментів

Якщо об’єкт дослідження (конструкції радіоелектронних засобів, технологічні процеси) допускає цілеспрямовану зміну всіх найбільш суттєвих вхідних змінних (факторів) за заздалегідь певним чином складеній програмі (матриці планування) в необхідних діапазонах варіювання, то для побудови математичної моделі об’єкту застосовується повний факторний експеримент. Отже, планування експерименту – це процедура вибору числа і умов проведення дослідів, необхідних і достатніх для отримання математичної моделі процесу. При цьому важливо враховувати наступне:

• прагнення до мінімізації числа дослідів;

• одночасне варіювання всіх змінних, які визначають процес;

• вибір чіткої стратегії, що дозволяє приймати обґрунтовані рішення після кожної серії дослідів.

Планування експерименту дозволяє варіювати ряд факторів і отримувати одночасно кількісні оцінки всіх ефектів, що проявляються.

Факторами будемо називати найбільш суттєві вхідні величини, отриманих в результаті експериментів [2], які приймають в деякий момент часу визначене значення. Область визначення фактору, тобто сукупності всіх значень, які прийме даний фактор, може бути неперервною або дискретною.

В задачах планування активного експерименту завжди використовується дискретні області визначення, а для факторів з дискретною областю визначення (температура, час і т.п.) вибираються дискретні множини рівнів. Крім того, фактор повинен бути керованим (підтримуваним постійним під час досліду або змінним по заданій програмі), однозначним (який не є функцією інших факторів), вимірюваним з достатньо високою точністю. В сукупності фактори повинні бути сумісними (їх комбінації мають здійснюватися і бути безпечними), між ними не повинно бути лінійної кореляції [1].

Як правило, при активному експерименті фактори варіюються на двох рівнях (верхньому “+” та нижньому “-”), відмінних від так званого базового рівня x_бj (j=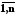) на значення кроку варіюванняx_j. В якості базового рівня можна вибрати величину фактору, визначену по технологічному регламенту або з міркувань професійно-логічного аналізу.

Дослід, в якому реалізуються всі можливі неповторювані сполучення рівнів факторів, називається повним факторним експериментом (ПФЕ). Кількість точок спостережень в цьому плані N=2ⁿ, де n – число факторів, які варіюються у двох рівнях. Умови експерименту представляються у вигляді таблиці, яка називається матрицею планування, де рядки відповідають різним дослідам, стовпці – значенням факторів.

Такий тип експерименту є оптимальним як з точки зору кількості дослідів, так і з точки зору повноти інформації, яку ми отримуємо в процесі експерименту.

Наприклад, для двох незалежних факторів n = 2 кількість дослідів N = 4.

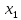та 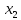- змінні параметри. Експеримент проводиться в досить вузькій обмеженій області навколо початкової точки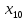та.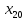

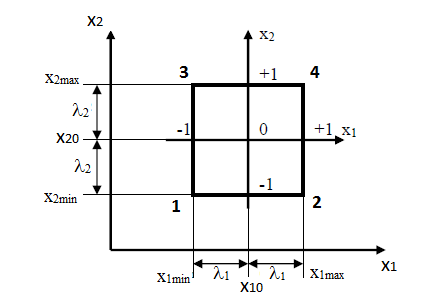
Зміна параметрів задається кроками варіювання, які позначатимемо ₁ та ₂. При цьому 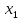та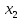можуть приймати значення:

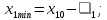
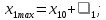
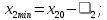
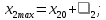
На перетині цих значень змінних отримуємо точки. Кожна точка відображає один дослід. Початкова точка участі в досліді не приймає.

На вибір інтервалу варіювання також накладаються обмеження: він не повинен бути менше похибки, з якою фіксується рівень фактору, та не може бути настільки великим, що верхній і нижній рівень опинилися за межами області визначення.

Формалізація системи позначень

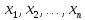Від системи координат необхідно перейти до нової безрозмірної системи координат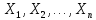за допомогою лінійного перетворення:

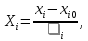
де 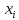- верхній або нижній рівень варіювання;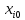- базовий рівень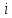- го фактора;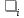- крок варіювання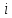- го фактора.

Формування активної частини матриці

В матриці планування верхньому рівню 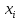відповідає «+1», а нижньому «-1» (для спрощення запису «+» та «-»). Координати центру дорівнюють нулю і співпадають з початком координат.

Таблиця 1

Номер досліду	х0	х1	х2	х1х2	Значення вихідного параметра
1	+	-	-	+	y1
2	+	+	-	-	y2
3	+	-	+	-	y3
4	+	+	+	+	y4

У відповідності з активною частиною матриці формується експеримент. В першому досліді значення факторів примусова виставляємо на нижньому рівні. В цій матриці жоден дослід не повторюється і жоден дослід не пропускається.

Фіктивно змінна та взаємодія параметрів

Для того, щоб відобразити початкову точку експерименту в першому стовпці матриці вводиться фіктивна змінна х₀. Фіктивна змінна в природі не існує. Це формальне значення в матриці планування дозволяє визначити початкову точку.

х₁х₂ – фіктивний добуток, якого в природі не існує, але він відображає взаємодію параметрів 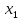та 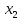(сумісну дію параметрів).

Особливості матриці планування

1. матриця планування є квадратною;

2. жоден стовбець і жоден рядок не повторюються.

Реалізувавши експеримент і отримавши значення 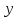будується математична модель у вигляді полінома:

,

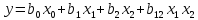яка представляє собою рівняння регресії – регресійна модель. Ця модель повністю відповідає матриці планування.

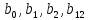- коефіцієнти регресії.

Кожен коефіцієнт регресії показує ступінь впливу лінійних факторів та їх взаємодії на вихідний параметр.

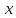- фактори.

Експеримент типу 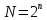називається повним факторним експериментом.

Порядковий номер стовпця – 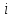, а досліду –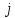. Кожен з дослідів в матриці планування буде мати індексацію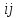. Коефіцієнти регресії визначаються за формулою:

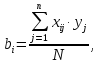
де 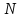- кількість дослідів.

Наприклад,

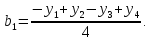
Побудова матриці планування типу .

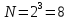Номер досліду	х0	х1	х2	х3	х1х2	х1х3	х2х3	х1х2 х3
1	+	-	-	-	+	+	+	-
2	+	+	-	-	-	-	+	+
3	+	-	+	-	-	+	-	+
4	+	+	+	-	+	-	-	-
5	+	-	-	+	+	-	-	+
6	+	+	-	+	-	+	-	-
7	+	-	+	+	-	-	+	-
8	+	+	+	+	+	+	+	+

Активна частина

матриці планування

При заповнені матриці частота зміни знаку кожного наступного параметра зменшується в два рази.

За результатами такого експерименту будується наступна математична модель:

,

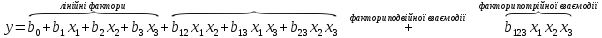Потрійна взаємодія в природі не існує.

Число дослідів в ПФЕ значно перевищує число коефіцієнтів моделі, які визначаються, що приводить до великої вибірковості дослідів. Було б оптимально скоротити їх число за рахунок тієї інформації, яка не дуже суттєва при побудові лінійних моделей, при цьому, щоб матриця планування не втратила своїх оптимальних властивостей. Одним із шляхів мінімізації числа дослідів є дробовий факторний експеримент. Надлишковість дослідів використовують для формування планів дробового факторного експерименту (ДФЕ).

Побудова дробових факторних експериментів

Дробовий факторний експеримент – це частина ПФЕ, який мінімізує число дослідів, за рахунок тієї інформації, яка не дуже істотна для побудови лінійної моделі. Для повного факторного експерименту типу 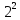рівняння регресії з урахуванням ефектів взаємодії можна представити залежністю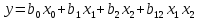. Для цього експерименту матрицю планування наведено в таблиці 1.

Таблиця 1.-Матриця планування для ПФЕ

№ досліду	x0	x1	x2	x1x2	y
1	+	-	-	+	y1
2	+	+	-	-	y2
3	+	-	+	-	y3
4	+	+	+	+	y4

При 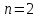побудова матриць повного факторного експерименту не викликає труднощів, тому що всі можливі сполучення рівнів факторів легко знайти простим перебором. При збільшенні числа факторів (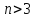) кількість можливих сполучень рівнів швидко зростає. Якщо при побудові моделі можна обмежитися лінійним наближенням

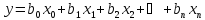, то число експериментів можна різко скоротити в результаті використання дробового факторного експерименту. Так, у повному факторному експерименті типу 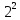при лінійному наближенні можна прийняти, що коефіцієнт лінійної моделі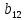дорівнює нулю, а стовпець 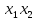матриці (таблиці 2) використовувати для третього фактору .

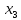Таблиця 2.-Матриця планування для ДФЕ

№ досліду	x0	x1	x2	x3 (x1x2)	y
1	+	-	-	+	y1
2	+	+	-	-	y2
3	+	-	+	-	y3
4	+	+	+	+	y4

При цьому, для визначення коефіцієнтів лінійної моделі

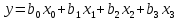
досить провести чотири експерименти замість восьми в повному факторному експерименті типу .

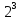Дробові репліки

Дробовою реплікою називають план експерименту, що є частиною плану повного факторного експерименту. Дробові репліки позначають , де

n - кількість експериментів;

p - число лінійних ефектів, які прирівнюють до ефектів взаємодії.

При p=1 одержують піврепліку; при p=2 одержують 1/4 репліку; при p=3 одержують 1/8 репліки і т.д. по ступенях двійки. Дробові репліки широко застосовують при одержанні лінійних моделей. Ефективність застосування дробових реплік залежить від вдалого вибору системи змішування лінійних ефектів з ефектами взаємодії. У зв'язку з тим, що в дробових репліках частину взаємодій замінено новими факторами, знайдені коефіцієнти рівняння регресії будуть спільними оцінками лінійних ефектів і ефектів взаємодії. Лінійні ефекти рекомендують змішувати, насамперед, з тими взаємодіями, які відповідно до апріорної інформації є незначущими. У випадку, коли ефекти взаємодії, хоча й малі в порівнянні з лінійними, але не дорівнюють нулю, необхідно заздалегідь визначити, які коефіцієнти є змішаними оцінками. Тоді залежно від умов поставленої задачі, підбирають таку дробову репліку, за допомогою якої можна отримати максимальну інформацію з експерименту. Доцільність їх застосування зростає із зростанням кількості факторів. Так, при дослідженні впливу 15 факторів можна в 2048 разів скоротити число експериментів, застосовуючи репліку великої дробності (16 дослідів замість 32768).

Частіше всього дробові репліки задають за допомогою генеруючих співвідношень.

Генеруючі співвідношення. Насичені плани

Генеруючим називають співвідношення, що показує, яку із взаємодій прийнято незначущою і замінено новим фактором. План типу 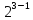може бути представлено двома піврепліками (таблиця 4), які задають одним з наступних генеруючих співвідношень:

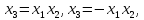
Генеруюче співвідношення помножимо на нову незалежну змінну :

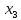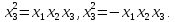
Тоді матриця планування буде представлена двома репліками:

№ досліду	x1	x2	x3	№ досліду	x1	x2	x3
1	-	+	-	1	-	+	+
2	+	+	+	2	-	+	+
3	-	-	+	3	-	-	-
4	+	-	-	4	+	-	+

Оскільки 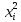, одержимо наступні співвідношення:

(****)

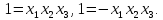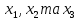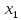У результаті множення генеруючого співвідношення на нову змінну одержують визначальний контраст. Для вказаних вище півреплік визначальними контрастами будуть залежності (****). За визначальним контрастом можна знайти співвідношення, що задають спільні оцінки. Для цього необхідно помножити незалежні змінні на визначальний контраст. При множенні визначальних контрастів (****) на, отримаємо співвідношення

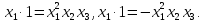
Оскільки 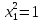, то

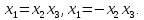
При множенні визначальних контрастів на 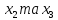, отримаємо співвідношення:

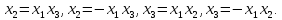
Це означає, що коефіцієнти лінійної моделі будуть оцінками параметрів:

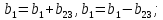
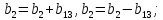
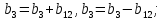
У практичних задачах потрійні і більш високого порядку взаємодії значно частіше, ніж подвійні, дорівнюють нулю і тому їх можна відкинути. Для отримання лінійної моделі рекомендують вибирати дробові репліки з можливо більшою роздільною здатністю, тобто репліки, у яких лінійні ефекти змішані з ефектами взаємодії близькими до нуля. При виборі дробової репліки важливо також ураховувати насиченість плану Піврепліки, в яких основні ефекти змішані з двофакторним добутком називаються насиченими планами з роздільною здатність III. При відсутній інформації про ефекти взаємодій двофакторного добутку експериментатор прагне вибрати репліку з найбільшою роздільною здатністю. Якщо існує якась інформація про ефекти взаємодій, то вона повинна використовуватись при виборі репліки. Також існують насичені плани з роздільною здатністю 4, репліки в яких всі парні взаємодії змішані між собою.

Ефективність реплік

• Ефективність репліки залежить від системи змішування. Репліки, у яких лінійні ефекти змішані з взаємодіями найвищого порядку, є найбільш ефективними, оскільки володіють найбільшою роздільною здатністю.

• Для звільнення лінійних ефектів від взаємодій першого порядку можна використовувати метод «перевалу». Сенс методу в додаванні нової репліки, всі знаки якої протилежні початковій репліці.

• Із зростанням числа факторів швидко збільшується число реплік різного дробу. Ці репліки характеризуються узагальнюючими визначальними контрастами, які виходять перемножуванням по два, по три і так далі початкових визначальних контрастів.