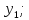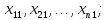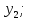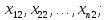Експериментальні методи дослідження конструкцій та технологічних процесів

Визначення коефіцієнтів впливу методом малих приростів

Маємо пристрій, якість функціонування якого описується вихідним параметром 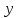. Значення вихідного параметра залежить від первинних параметрів 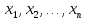. Між ними має існувати функціональний зв'язок, але нам не відомо який. Знаємо, що похибки вихідного параметра зв’язана з похибками первинних параметрів рівнянням похибок:

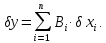
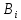- невідомі коефіцієнти впливу.

Задача полягає в тому, щоб визначити коефіцієнти впливу при умові, що рівняння функціонального зв’язку нам не відоме.

В методі малих приростів створюється модель об’єкта, яка дозволяє плавно чи дискретно змінювати кожен з вхідних параметрів в певному діапазоні значень.

В початковому стані встановлюються відхилення всіх параметрів = 0. Тоді всі

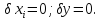
Одному з вхідних параметрів надається невеликий приріст (відхилення від номінального значення) порядку 10%. Отже, 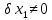і рівняння похибок буде мати вигляд:

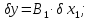
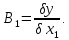
Аналогічно визначаються коефіцієнти впливу всіх інших вхідних параметрів.

Цей метод знаходить застосування на ранніх стадіях проектування ЕА (на стадії ескізного проектування), коли відпрацьовуються електричні схеми з їх макетуванням.

Цей метод має ряд суттєвих недоліків, які полягають в наступному:

1. метод не дозволяє визначити коефіцієнти впливу параметрів, між якими існують кореляційні зв’язки;

2. при низькій чутливості зміни вихідного параметра 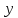до зміни вхідних параметрів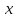для визначення коефіцієнту впливу необхідно задавати великий приріст цьому параметру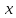і це може бути фізично неможливим, або такий приріст призводить до порушення функціонування об’єкта в цілому.

Метод імітації відхилень параметрів

Даний метод застосовується на стадії розробки дослідних взірців та на більш пізніх стадіях – стадіях конструкторської документації. Суть метода полягає в наступному.

Маємо об’єкт, вихідний параметр 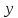якого залежить від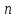вхідних параметрів.

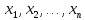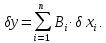
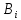- невідомі коефіцієнти впливу.

Довільно вибираємо 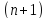виріб даного типу, тобто на один більше, ніж число вхідних параметрів. Один з цих виробів умовно вважаємо еталонним або базовим і значення всіх параметрів цього виробу приймаємо за номінальні. Позначимо ці параметри:

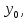
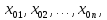де індекс «0» означає значення параметрів нульового рівня.

Аналогічно можемо визначити значення параметрів всіх інших взірців і ці значення записати:

1. 

2. 

………………………….

.

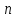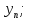
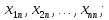
Для 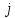– го значення:

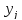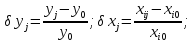
Можна записати систему з 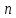рівнянь з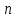невідомими коефіцієнтами впливу:

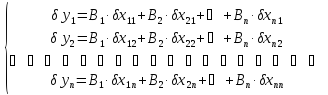
Розв’язуючи цю систему рівнянь отримуємо значення всіх коефіцієнтів впливу.

Метод застосовується на пізніх стадіях конструкторського проектування, тому коректування структури параметрів виробу є більш складною задачею. Кореляція тут не відіграє суттєвого значення.

Метод граничних випробувань

Даний метод використовується для дослідження стабільності функціонування електронних засобів шляхом імітації впливу певних дестабілізуючих факторів. В теорії надійності даний метод використовується для оцінки надійності за поступовими відмовами.

Зазвичай дослідження починаються з визначення границь для кожного з вхідних (змінних) параметрів, в межах яких кожен вихідний параметр задовольняє технічним вимогам і систему можна вважати працездатною. Результати граничних випробувань повністю визначають конфігурацію і положення допустимих значень у факторному просторі, якщо обмеження обумовлені тільки технічними вимогами. У більш складних випадках необхідно враховувати не тільки працездатність, а й інші показники, наприклад, економічні, показники надійності та стабільності роботи та ін.. В цих умовах результати граничних випробувань доповнюють обмеження, що витікають із вимог до даних показників.

Будь-який радіоелектронний пристрій характеризується деякою сукупністю вихідних параметрів. До них відносяться, наприклад, напруга живлення, потужність, робоча частота, коефіцієнт підсилення, характеристики частотних, фазових, нелінійних спотворень підсилювача та ін.

Якщо вихідні параметри знаходяться в допустимих межах, то пристрій вважається працездатним, в іншому випадку фіксується відмова.

Припустимо, що математична модель системи відома і представлена у вигляді функціональної залежності

.

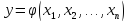Якщо поле допуску на вихідний параметр задано інтервалом 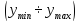, то умова працездатності системи полягає в тому, що величина вихідного параметра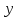повинна знаходитись в допустимих межах:

. (***)

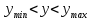Ця умова називається критерієм працездатності системи. Область значень параметрів елементів, при якій виконується дана умова, називається областю працездатного стану пристрою (областю надійної роботи). Вочевидь, що границі області працездатного стану визначаються з (***), якщо замінити знаки нерівності на знаки рівності:

,

…………………………

.

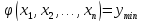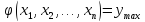Кожне з цих рівнянь описує поверхню в 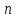- мірному просторі.

Метод граничних випробувань базується на припущенні, що вихідний параметр представляє собою монотонну функцію багатьох змінних параметрів. При моделюванні експериментальним шляхом визначаються перетини даної функції по кожному з параметрів, тобто, знаходяться допустимі границі зміни цих параметрів в залежності від обраного параметра граничних випробувань.

Дана методика складається з наступних етапів:

1. Визначення критерію працездатності системи (критерію граничних випробувань);

2. Вибір параметра граничних випробувань;

3. Оцінка часткових областей працездатності системи по кожному з вимірюваних параметрів;

4. Аналіз результатів випробувань і розробка рекомендацій по коректуванню параметрів системи.

Суть методу полягає в наступному.

Для проведення граничних випробувань створюється макет об’єкту з можливістю плавної чи дискретної зміни всіх параметрів, які визначають роботу пристрою: .

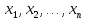В якості критерію граничних випробувань використовується умова (***).

Один з цих параметрів вибираємо в якості базового або граничного. До цього параметра висуваються наступні вимоги:

1. Вплив цього параметра на вихідний параметр системи повинен бути визначальним, тобто, вихідний параметр повинен мати високу чутливість до зміни базового параметру;

2. Він повинен бути незалежним, або слабо залежним від інших параметрів системи, тобто, базовий параметр не повинен бути зв’язаним кореляційними зв’язками із жодним іншим параметром.

3. Базовий параметр повинен допускати, по можливості, плавну зміну в достатньо широких межах;

4. Його зміна у вказаних межах не повинна змінювати параметри інших елементів системи.

Проведення експерименту.

1. Значення вхідних параметрів встановлюють рівним номінальним.

2. Базовий параметр плавно змінюється в одну сторону до тих пір, поки не буде порушена умова працездатності, тобто, поки значення вихідного параметра не вийде за встановлені межі. Потім аналогічно змінюємо в іншу сторону. Отримаємо дві точки поверхні.

3. Надаємо дискретний приріст базовому параметру і процедуру повторюємо, фіксуючи порушення умови працездатності. Дискретний приріст надаємо у додатну і у від’ємну сторони.

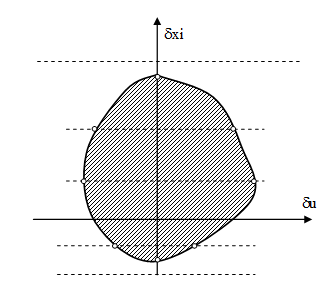
Утворена фігура обмежує область працездатності системи. Аналогічним чином будуються області працездатності для всіх вхідних параметрів в комбінації з базовим.

Отримані області накладаються одна на одну і отримаємо область працездатності по всім параметрам.

Побудована область дає можливість дослідити діапазон змін параметрів. Конфігурація і положення області працездатності відносно початку координат дає можливість зробити висновки про досконалість прийнятого рішення, і в певній мірі, оптимізувати технічне рішення. Отримана картина значень дозволяє легко визначати коефіцієнти впливу.

Недоліки даного методу:

• велика трудоємність проведення експериментальних досліджень.

• наявність кореляційних зв’язків не дозволяє побудувати об’єктивну область працездатності.

Метод матричних випробувань

Подальшим розвитком методу граничних випробувань є матричні випробування, які дозволяють вилучити можливі хибні висновки і рекомендації по коректуванню номіналів елементів, отриманих при аналізі графіків працездатності.

Метод матричних випробувань – це метод фізичного моделювання. Він дозволяє визначити робочу область пристрою при всіх можливих значеннях первинних параметрів, що знаходяться в межах допусків, оптимізувати його працездатність.

Первинні параметри можна розбити на наступні групи:

• Параметри деталей, з яких складається пристрій;

• Параметри джерел живлення;

• Параметри вхідних сигналів;

• Параметри навантаження;

• Параметри, що характеризують умови оточуючого середовища.

Суть методу матричних випробувань і задачі оцінки та оптимізації працездатності за результатами цих випробувань розглянемо на прикладі пристрою, працездатність якого суттєво залежить тільки від двох первинних параметрів 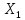та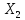. Такі параметри будемо називативизначаючими первинними параметрами.

Нехай діапазон можливої зміни цих параметрів заданий інтервалами 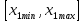та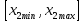. Розіб’ємо інтервали н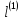ата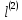рівних квантів відповідно.

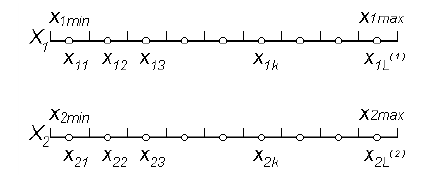
Приклад розбиття параметрів 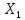та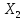на кванти

В якості представників квантів виберемо значення параметрів, що відповідають серединам квантів. Якщо пристрій виявляється непрацездатним (працездатним) при значенні параметрів, що відповідають представнику кванта, то будемо вважати, що він не працює (працює) при всіх значеннях параметрів, що лежать в цьому кванті.

Вводимо поняття ситуації, під яким будемо розуміти такий стан пристрою, коли кожен з його двох визначаючих параметрів (двовимірний випадок) приймає значення, що відповідає представнику визначеного кванта. Це визначення легко розповсюдити на 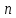- мірний випадок. Число всіх можливих ситуацій пристрою в двовимірному випадку дорівнює:

.

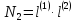Індекс 2 при 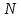означає, що розглядає двовимірний випадок, тобто маємо два визначаючі параметри. В загальному випадку при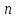визначаючих параметрах число можливих ситуацій дорівнює:

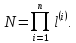
Перебрав в будь-якій послідовності всі несумісні ситуації пристрою, складаємо матрицю ситуацій. Для двовимірного випадку вона буде мати вигляд:

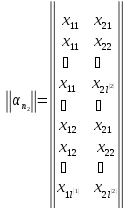
В матриці другий рядок 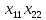, наприклад, означає, що параметр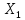прийняв значення в першому, а параметр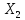- у другому кванті.

Впорядковану таким чином послідовність всіх можливих ситуацій пристрою позначимо

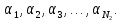
Серед 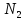можливих ситуацій пристрою при матричних випробуваннях буде виявлена деяка кількістьQ відмовних ситуацій з точки зору заданого критерію відмови пристрою, що розглядається. Відмовні ситуації будемо відмічати рискою зверху. Вони можуть бути визначені натурним фізичним моделюванням, оскільки таке моделювання дозволяє досить точно відтворити роботу пристрою і автоматично врахувати всі фактори, що впливають на його працездатність, в тому числі і другорядні, які при всіх інших видах моделювання, як правило, не враховуються.

Результати матричних випробувань дозволяють знайти область працездатності пристрою (рис), ймовірність знаходження вихідного параметра в межах поля допуску і оптимізувати працездатність.

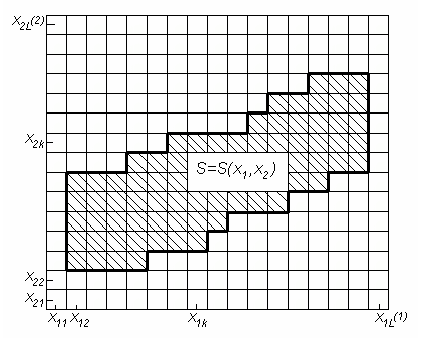
Область працездатності

Для порівняльної оцінки ймовірність працездатності пристрою, що досліджується, визначається за формулою:

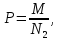
де 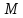- кількість ситуацій, в яких пристрій був працездатним;

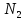- загальна кількість ситуацій.

Перевага метода матричних випробувань – можливість кількісної оцінки працездатності.

Недолік – значна тру ємність і складність використання для пристроїв, у яких моделювання первинних параметрів забруднено.