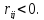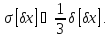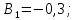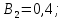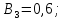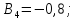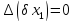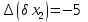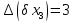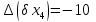- •Основи точності та надійності електронних апаратів частина і. Основи теорії надійності електронних засобів
- •Елементи теорії ймовірності
- •Показники надійності
- •Теоретичні розподіл часу напрацювання до відмови
- •Надійність типових елементів
- •Методи розрахунку надійності
- •Орієнтовні методи розрахунку надійності
- •Уточнений або повний розрахунок надійності
- •Показники довговічності
- •Показники відновлюваності (ремонтопридатності)
- •Комплексний показник надійності
- •Методи забезпечення надійності
- •Конструкторсько-технологічні методи підвищення надійності
- •Класифікація способів резервування
- •Класифікаційна таблиця способів резервування
- •Аналіз надійності системи з загальним постійним резервом
- •Аналіз надійності системи з постійним роздільним резервуванням
- •Частина іі. Основи точності та стабільності функціонування еа
- •Методи аналізу точності функціональних вузлів
- •Імовірнісний метод аналізу точності
- •Експериментальні методи дослідження конструкцій та технологічних процесів
- •Планування експериментів
Імовірнісний метод аналізу точності
Імовірнісний метод аналізу точності використовує елементи теорії ймовірності. Тому спочатку слід нагадати деякі основні визначення та теореми теорії ймовірності.
Системи випадкових величин
Сукупність
випадкових величин
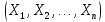 які розглядаються спільно, називаєтьсясистемою
n випадкових величин.
Якщо n
= 2, тобто розглядається система двох
випадкових величин
які розглядаються спільно, називаєтьсясистемою
n випадкових величин.
Якщо n
= 2, тобто розглядається система двох
випадкових величин
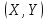 ,
то геометрично її можна тлумачити як
випадкову точку з координатами
,
то геометрично її можна тлумачити як
випадкову точку з координатами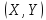 на площині
на площині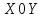 або як випадковий вектор, складові якого
— випадкові величини.
або як випадковий вектор, складові якого
— випадкові величини.
Функцією
розподілу системи двох випадкових
величин
називається функція двох аргументів
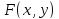 ,
яка дорівнює ймовірності сумісного
виконання двох нерівностейX
< x
і Y
< y,
тобто:
,
яка дорівнює ймовірності сумісного
виконання двох нерівностейX
< x
і Y
< y,
тобто:
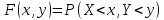
Якщо
події
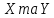 незалежні, то:
незалежні, то:
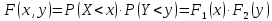 ;
;
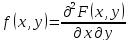
Функцію
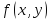 називають густиною розподілу ймовірностей
системи неперервних випадкових величин
називають густиною розподілу ймовірностей
системи неперервних випадкових величин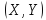 .
.
Для незалежних випадкових величин:
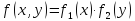 .
.
Числові характеристики функцій випадкових аргументів
Система
з двох випадкових величин
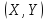 має два математичні сподівання (два
центральні моменти):
має два математичні сподівання (два
центральні моменти):
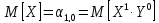 -
математичне сподівання добутку двох
випадкових величин;
-
математичне сподівання добутку двох
випадкових величин;
Для неперервних випадкових величин:
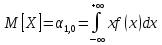
-
математичне сподівання
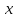 в системі
в системі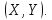
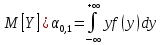
-
математичне сподівання
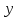 в системі
в системі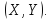
Система
з двох випадкових величин
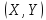 має три центральні моменти:
має три центральні моменти:
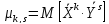
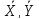 –значення
випадкових величин
–значення
випадкових величин
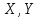 .
.
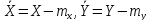
де
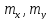 - математичні сподівання
- математичні сподівання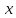 та
та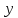 відповідно.
відповідно.
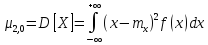
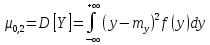
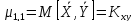 -
кореляційний момент.
-
кореляційний момент.
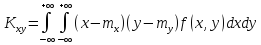
Для незалежних випадкових величин
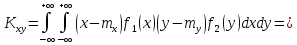
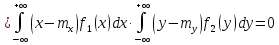
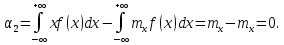
Для незалежних випадкових величин перший центральний момент завжди =0, тому і кореляційний момент буде =0.
Отже, кореляційний момент є характеристикою ступеня ймовірної залежності між випадковими величинами.
Кореляційний момент описує ступінь тісноти імовірнісного зв’язку між випадковими величинами. Кореляція може існувати тільки між парами величин. Між трьома і більше параметрів кореляція існувати не може. Кореляційний момент описує також розсіювання і тому він не може бути чисельною мірою зв’язку між величинами.
Коефіцієнт кореляції визначається за формулою:
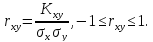
Кореляція – лінійний імовірнісних зв'язок між двома величинами, коли зміна однієї з величин викликає тенденцію до лінійної зміни іншої величини.
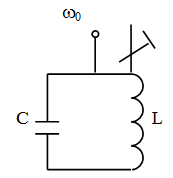
Приклад.
Дано коливальний контур, який забезпечує
певну частоту коливань
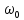 .
.
При
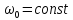 індуктивність є функцією ємності.
індуктивність є функцією ємності.
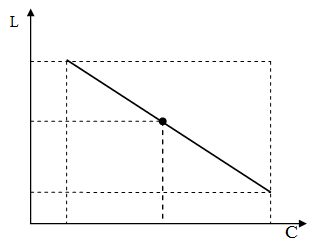
В
реальному випадку
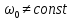 ,
тому будуть виникати певні похибки. В
результаті отримаємо:
,
тому будуть виникати певні похибки. В
результаті отримаємо:
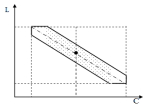
|
|
Лінія регресії – це залежність математичного сподівання L(C). Ширина діапазону залежить від точності настройки.
|
|
|
Наявність кореляції є шкідливою, оскільки вона завжди впливає на точність процесів, розширює поле допуску, надзвичайно затрудняє експериментальні дослідження.
|
Теореми про числові характеристики функцій випадкових аргументів
Випадкові аргументи завжди розглядаються як система випадкових величин.
Теорема 1. Математичне сподівання невипадкової величини дорівнює самій величині.
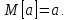
Теорема 2. Дисперсія невипадкової величини дорівнює 0.
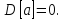
Теорема 3. Невипадкову величину можна вивести з-під знаку математичного сподівання.
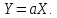
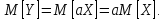
Теорема 4. Невипадкову величину можна вивести з-під знаку дисперсії, підносячи її до квадрату.
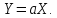
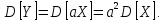
Теорема 5. Математичне сподівання суми випадкових величин дорівнює сумі математичних сподівань цих величин.
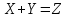
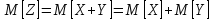
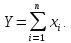
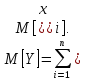
Теорема 6. Дисперсія суми двох випадкових величин дорівнює сумі їх дисперсій плюс подвоєний кореляційний момент.
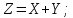
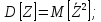
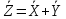 .
.
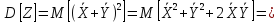
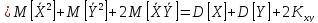
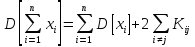
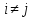 під
знаком
означає, що додаються всі можливі
кореляційні моменти, які існують в
системі.
під
знаком
означає, що додаються всі можливі
кореляційні моменти, які існують в
системі.
Загальна
кількість кореляційних моментів в
системі з n
величин:
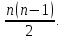
Теорема 7. Математичне сподівання лінійної функції дорівнює тій же лінійній функції від математичних сподівань аргументів.
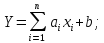
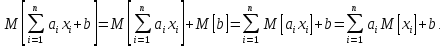
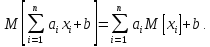
Теорема 8. Дисперсія лінійної функції:
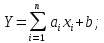
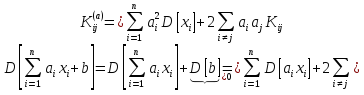
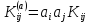 -
кореляційний момент з урахуванням
-
кореляційний момент з урахуванням
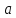 .
.
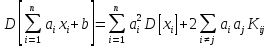
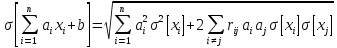
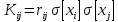 .
.
Розрахунок характеристик поля допуску на вихідний параметр
Повинні встановити зв'язок між числовими характеристиками випадкової величини і відповідними характеристиками поля допуску. Цей зв'язок базується на виразах, отриманих раніше. Необхідно встановити зв'язок між математичним сподівання та координатою середини поля допуску та між середньоквадратичним відхиленням та половиною поля допуску.
Зв'язок між математичним сподіванням та координатою середини поля допуску
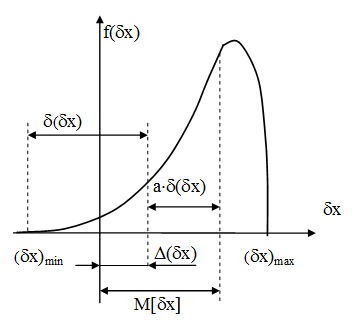
Для встановлення зв’язку між математичним сподівання та координатою середини поля допуску використовується коефіцієнт відносної асиметрії кривої розподілу похибки в полі допуску:
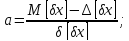
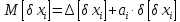 ;
;
Для вихідного параметра:
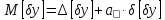 ;
;
Коефіцієнт
відносної асиметрії
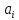 залежить від закону розподілу похибки
первинного параметра в полі допуску:
залежить від закону розподілу похибки
первинного параметра в полі допуску:
для симетричного закону розподілу
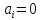 ;
;для право симетричної кривої
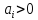 ;
;для ліво симетричної кривої
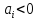 .
.
Основне рівняння похибок має вигляд:
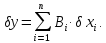
Оскільки це лінійна функція, то застосовуємо теорему про математичне сподівання лінійної функції (Т.7):
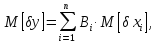
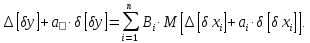
Згідно
з центральною граничною теоремою,
похибка вихідного параметра буде мати
закон розподілу близький до нормального
і симетричний (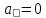 ),
тоді:
),
тоді:
Координата середини поля допуску вихідного параметра буде дорівнювати:
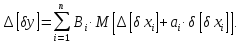
Коефіцієнти
відносної асиметрії
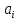 для різних законів розподілу визначається
з довідникових таблиць.
для різних законів розподілу визначається
з довідникових таблиць.
Зв'язок між середньоквадратичним відхиленням та половиною поля допуску
|
|
Для нормального закону розподілу справедливо правило 3, згідно з яким:
Це справедливо з ймовірністю Р = 0,9973. |
Отже
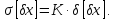
Коефіцієнт
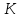 вираховується по відношенню до нормального
закону розподілу і називається
коефіцієнтом відносного розсіювання
похибки в полі допуску.
вираховується по відношенню до нормального
закону розподілу і називається
коефіцієнтом відносного розсіювання
похибки в полі допуску.
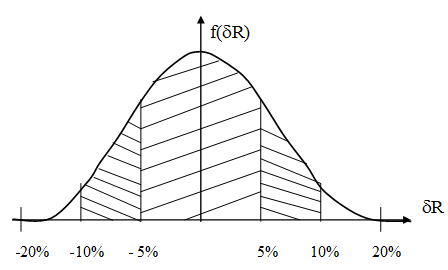
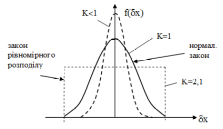
Рис. . загальний закон розподілу
|
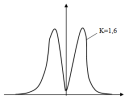
для 10% - резисторів |
для 20% - резисторів |
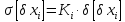
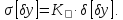
Коефіцієнт
відносного розсіювання
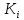 залежить від закону розподілу первинних
параметрів. При нормальному законі
розподілу
залежить від закону розподілу первинних
параметрів. При нормальному законі
розподілу
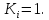 для елементів масового застосування:
для елементів масового застосування:
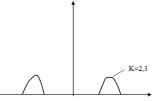
Для
5% елементів
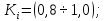
Для
10% елементів
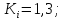
Для
20% елементів
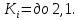
Для
10% елементів
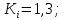
Для
решти елементів
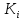 визначається за формою закону розподілу.
Наприклад, для рівноймовірного закону
визначається за формою закону розподілу.
Наприклад, для рівноймовірного закону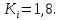
Основне рівняння похибок:
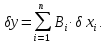
Застосовуючи теорему про дисперсію (середньоквадратичне відхилення) лінійної функції, отримаємо зв'язок між половиною поля допуску вихідного та вхідних параметрів:
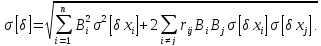
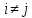 під
знаком
означає, що додаються всі можливі попарні
комбінації випадкових параметрів.
під
знаком
означає, що додаються всі можливі попарні
комбінації випадкових параметрів.
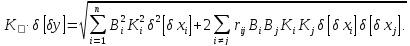
Вихідний
параметр розподілений за нормальним
законом, тому
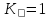 з ймовірністю Р = 0,9973. Тому вводиться
додатковий коефіцієнт гарантованої
достовірності розрахунку допуску(Pr).
з ймовірністю Р = 0,9973. Тому вводиться
додатковий коефіцієнт гарантованої
достовірності розрахунку допуску(Pr).
Наприклад: Pr = 0,9973 = 1.
Pr = 0,999 = 1,04.
Pr = 0,9999 = 1,1.
Половина поля допуску вихідного параметра для будь-якого випадку – загальний вигляд:
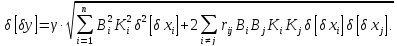
Проведемо розрахунок поля допуску для попереднього прикладу ймовірнісним методом.
Приклад. Визначити допуск на вихідний параметр.
Коефіцієнти
впливу:
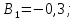
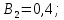
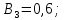
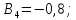
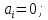
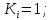 -
всі похибки розподілені за нормальним
законом.
-
всі похибки розподілені за нормальним
законом.
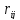 -
відсутні кореляційні зв’язки між
параметрами.
-
відсутні кореляційні зв’язки між
параметрами.
|
|
|
= 1;
|
Розв’язання
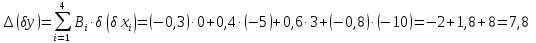
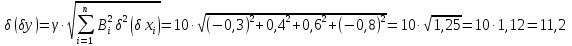
Поле допуску за методом найгіршого випадку:
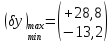 %.
%.
Переваги ймовірнісного методу:
Цей метод дає можливість отримати безпосередньо залежності між характеристиками поля допуску.
Дозволяє легко змінювати точність розрахунку шляхом зміни
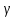 .
.
Недолік: громіздкість розрахункових формул.
Загальне поле допуску вихідного параметра буде мати вигляд:
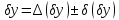 .
.
До сих пір при аналізі поля допуску ми не розглядали суті похибок. Ці вирази будуть справедливі для будь-яких похибок.
Розрахунок температурного поля допуску
Вплив температури приводить до зворотних, а інколи і до незворотних змін параметрів. Розглянемо випадок, коли зміни зворотні. В цьому випадку чутливість параметрів до зміни температури прийнято характеризувати температурним коефіцієнтом:
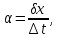
який
представляє собою відносну зміну
параметра при зміні температури на
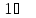 .
.
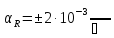 -
температурний коефіцієнт резистора.
-
температурний коефіцієнт резистора.
Температурний коефіцієнт представляє лінійний коефіцієнт пропорціональності функції зміни параметру від температури. На практиці така зміна часто носить нелінійний характер.
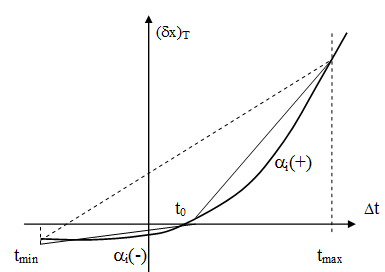
Для
того, щоб не допускати похибки при
апроксимації, цю криву апроксимують
двома прямими. За номінальне значення
температури приймають
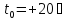 .
Тоді будь-який параметр характеризується
2-ма температурними коефіцієнтами:
.
Тоді будь-який параметр характеризується
2-ма температурними коефіцієнтами:
температурний коефіцієнт
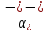 для
діапазону температур
для
діапазону температур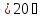 ;
;температурний коефіцієнт
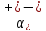 для
діапазону температур
для
діапазону температур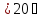 ;
;
В загальному випадку температурний коефіцієнт є випадковою величиною, тобто, будемо мати не одну криву, а сімейство кривих.
Таким чином, температурна похибка також є випадковою величиною. Частіше температурний коефіцієнт або температурна похибка підпорядковані нормальному закону розподілу.
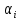 -
температурний коефіцієнт
-
температурний коефіцієнт
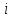 - того вхідного параметра.
- того вхідного параметра.
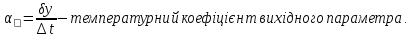
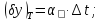
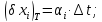
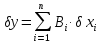
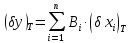
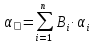
Температурні коефіцієнти мають систематичні і випадкові складові:
Конденсатор КТ-4-М47-100пФ±10%;
М47 – температурний коефіцієнт, М означає «-»;
М47
(-47 ± 30)10-6
1/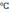 ;
;
-47 – систематична складова;
30 – випадкова складова.
Якщо П – це означає «+», Н – «±».
Систематичні та випадкові складові температурних коефіцієнтів викликають систематичні та випадкові похибки параметрів.
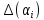 -
систематична складова вхідного параметра;
-
систематична складова вхідного параметра;
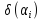 -
випадкова складова вхідного параметра.
-
випадкова складова вхідного параметра.
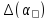 -
систематична складова вихідного
параметра;
-
систематична складова вихідного
параметра;
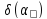 -
випадкова складова вихідного параметра.
-
випадкова складова вихідного параметра.
Систематична складова похибок нормується координатою середини поля допуску, а випадкова складова – половиною поля допуску.
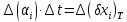 -
координати середини поля температурного
допуску вхідного параметру;
-
координати середини поля температурного
допуску вхідного параметру;
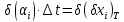 -
координата половини поля температурного
допуску вхідного параметру.
-
координата половини поля температурного
допуску вхідного параметру.
Температурний коефіцієнт залежить від приросту температури (чи вліво, чи вправо).
За
номінальне значення температури
приймають
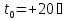 .
.
Температурний
діапазон задається двома граничними
значеннями температур
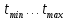 .
Тоді прирости температур визначаються
за формулами:
.
Тоді прирости температур визначаються
за формулами:
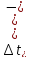
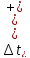
Залежність похибки від температури є нелінійною. Температурний коефіцієнт є лінійним.
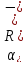
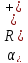
Враховуючи,
що температурні похибки, а значить і
температурні коефіцієнти, розподілені
за нормальним законом і коефіцієнт
відносної асиметрії розподілу
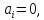 а коефіцієнт відносного розсіювання
а коефіцієнт відносного розсіювання
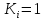 ,
отримаємо:
,
отримаємо:
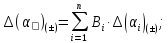
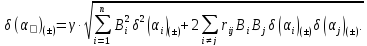
Індекс
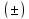 означає, що розрахунок виконується
окремо для температурних коефіцієнтів
в додатних та від’ємних приростах
температури.
означає, що розрахунок виконується
окремо для температурних коефіцієнтів
в додатних та від’ємних приростах
температури.
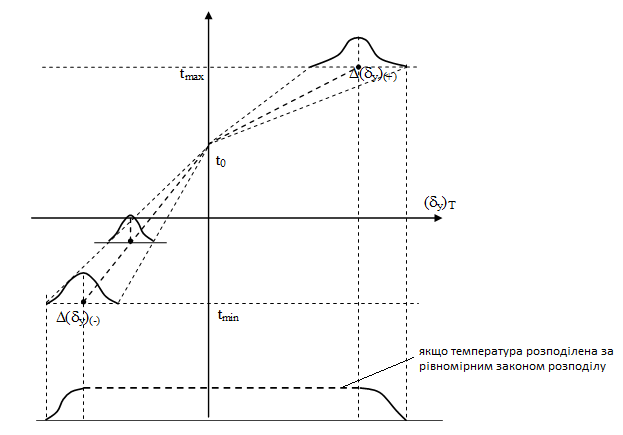
Характеристики поля температурного допуску на вихідний параметр визначаються за формулами:
координата середини поля температурного допуску на вихідний параметр:
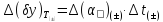 ;
;
координата половини поля температурного допуску на вихідний параметр:
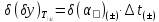 ;
;
Все поле температурного допуску:
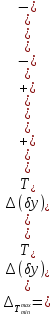 .
.
Розрахунок поля допуску на старіння
Похибки старіння кількісно характеризуються лінійним коефіцієнтом старіння.
Коефіцієнт старіння – відносна похибка параметра, яка виникає на протязі одиниці часу експлуатації:
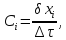
де
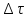 - проміжок часу, на протязі якого
визначають коефіцієнт старіння
- проміжок часу, на протязі якого
визначають коефіцієнт старіння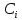 ;
;
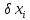 -
похибка старіння.
-
похибка старіння.
Для
резисторів
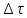 = 2000 год.,
= 2000 год.,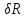 = ±3%;
= ±3%;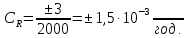
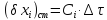 ,
де
,
де
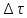 - час експлуатації виробу.
- час експлуатації виробу.
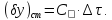
У загальному випадку
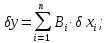
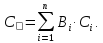
Поле допуску коефіцієнта старіння має систематичну і випадкову складові:
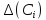 -
систематична складова коефіцієнта
старіння;
-
систематична складова коефіцієнта
старіння;
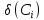 -
випадкова складова коефіцієнта старіння.
-
випадкова складова коефіцієнта старіння.
Враховуючи,
що похибки старіння, а значить і
коефіцієнти старіння, розподілені за
нормальним законом і для них коефіцієнт
відносної асиметрії розподілу
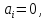 а коефіцієнт відносного розсіювання
а коефіцієнт відносного розсіювання
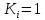 ,
отримаємо:
,
отримаємо:
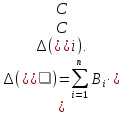
де
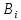 - коефіцієнти впливу.
- коефіцієнти впливу.
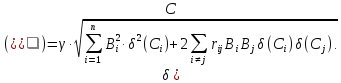
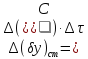 -
координата середини поля допуску на
старіння;
-
координата середини поля допуску на
старіння;
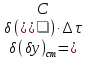 -
координата половини поля допуску на
старіння;
-
координата половини поля допуску на
старіння;
Граничні відхилення допуску старіння на вихідний параметр:
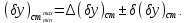
Розрахунок допуску на зволоження
Похибки зволоження кількісно характеризуються коефіцієнтом зволоження.
Коефіцієнт зволоження являє собою відносну похибку зволоження, що виникає при тривалій експлуатації в певних умовах підвищеної вологості.
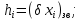
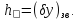
Для
резистора при рівні підвищеної вологості
95% при
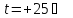 (що відповідає кліматичному виконанню
УХЛ) опір резистора змінюється на
величину
(що відповідає кліматичному виконанню
УХЛ) опір резистора змінюється на
величину
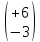 %
= (+1,5 ± 4,5)%.
%
= (+1,5 ± 4,5)%.
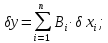
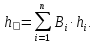
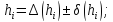
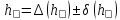 .
.
Систематична складова коефіцієнта зволоження:
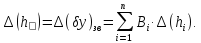
Випадкова складова коефіцієнта зволоження (половина поля допуску):
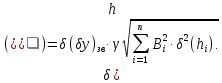
Допуск на зволоження:
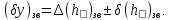
Похибки зволоження розподілені за нормальним законом, тому коефіцієнт відносної асиметрії розподілу
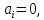 а коефіцієнт відносного розсіювання
а коефіцієнт відносного розсіювання
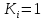 ;
;Похибки зволоження існують лише для параметрів негерметизованих елементів (резистори, конденсатори). Для герметизованих активних елементів (діоди, транзистори, мікросхеми) похибки зволоження = 0.
Кореляційні зв’язки можуть існувати тільки між параметрами активних елементів. Таким чином, друга складова суми під знаком кореня = 0.
Розрахунок виробничого поля допуску
Враховуючи, що виробничі похибки вхідних параметрів розподіляються за довільними законами, то для розрахунку виробничого допуску використовуються загальні формули координати середини і половини поля допуску.
Координата середини виробничого допуску:
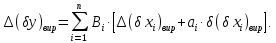
Половина поля виробничого допуску:
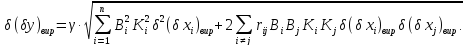
Загальне поле виробничого допуску записується у вигляді:
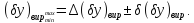
Розрахунок сумарного поля допуску на вихідний параметр
Розрахувавши частково характеристики виробничого та експлуатаційних допусків ми отримаємо певну кількість значень координат середин поля допуску та половин поля допуску відповідно.
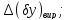
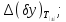
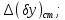
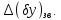
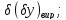
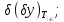
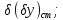
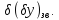
Необхідно отримати характеристики поля допуску на вихідний параметр з врахуванням всіх дестабілізуючих факторів.
Правило 1.
При розрахунку сумарного поля допуску координати середин поля допуску (систематичні складові) додаються алгебраїчно, уникаючи компенсації знаків. Тобто, додатні значення координат додаються окремо, від’ємні – окремо. Таким чином. Отримаємо два значення сумарних координат поля допуску:
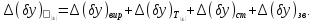
Індекс
( )
означає, що окремо додаються додатні
значення та окремо - від’ємні.
)
означає, що окремо додаються додатні
значення та окремо - від’ємні.
Правило 2.
Половини поля допусків додаються квадратично, тобто як корінь квадратний із суми квадратів:
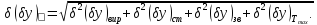
Задачі точності і стабільності можуть розглядатися як задачі аналізу та задачі синтезу (пряма та обернена задачі).
Задача аналізу полягає в тому, що є сформований і відомий об’єкт і за відомою інформацією про вхідні параметри розраховуються часткові та сумарний допуски на вихідний параметр, тобто, аналізується точність і стабільність виробу.
Задача синтезу полягає в тому, що для відомого об’єкта необхідно вибрати типи елементів та їх характеристики точності і стабільності, що задовольнити вимогу на допуск вихідного параметра.