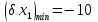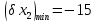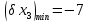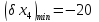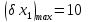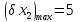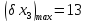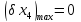Методи аналізу точності функціональних вузлів

Всі методи аналізу точності базуються на одних й тих самих рівняннях похибок.

Вихідні рівняння для аналізу точності

Будемо вважати, що відоме рівняння функціонального зв’язку між вихідним та вхідними параметрами ФВ.

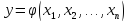
Це рівняння може бути задано аналітично, особливо у випадку, коли ФВ не складний.

Необхідно встановити зв'язок між похибками вхідних та вихідних параметрів.

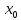- номінальне значення вхідного параметра ;

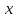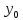- номінальне значення вихідного параметра .

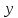Як би 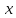не був випадковою величиною, то все було б добре. Але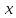приймає область значень

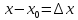
Відповідно і вихідний параметр 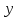буде приймати область можливих значень

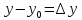
Необхідно встановити зв'язок між абсолютними похибками 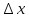та.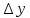

Умова.

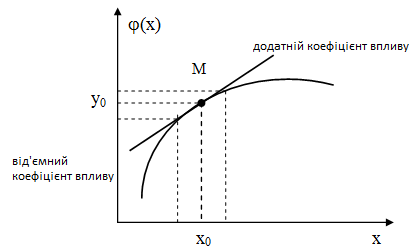
Діапазон можливих значень первинних параметрів повинен бути достатньо вузьким. У цьому випадку дотична у точці буде не дуже відходити від самої кривої. Рівняння дотичної у точці, що відповідає номінальним (розрахунковим) значенням параметрів, буде мати вигляд:

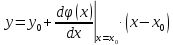
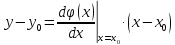
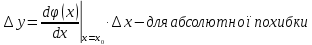
Вже відзначалось, що більший інтерес представляє собою відносні похибки.

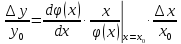
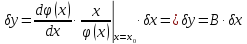
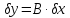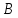- основне рівняння похибок для одного параметра. – коефіцієнт впливу похибки вхідного параметра на похибку вихідного параметра (коефіцієнт пропорційності).

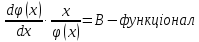
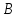- постійна величина, оскільки похідна береться в одній точці. Коефіцієнт впливу може бути і додатнім і від’ємним, і дорівнювати 0.

Як правило, вихідний параметр від множини первинних параметрів:

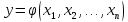
Позначимо 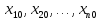- координати початкової точки. Тоді рівняння гіперплощини буде мати вигляд:

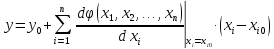
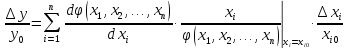
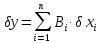
де

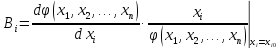
коефіцієнт впливу похибки і-го вхідного параметра на похибку вихідного параметра.

Приклад.

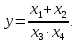
Знайти коефіцієнт впливу кожного параметра х.

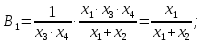
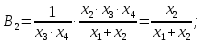
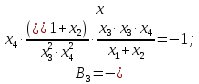
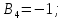
Для того, щоб визначити коефіцієнти впливу, необхідно знати рівняння функціонального зв’язку між первинними та вихідними параметрами.

У більшості випадків це рівняння невідоме. У випадку, коли рівняння функціонального зв’язку невідоме, застосовуються експериментальні методи визначення коефіцієнтів впливу.

Числові значення відносних коефіцієнтів впливу знаходяться в межах від -1 до +1 і проходять через 0.

У випадку степеневих функцій числове значення 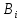може бути 1.

Основним завданням теорії точності є зменшення похибок вихідних параметрів. Це досягається трьома шляхами.

1. Шляхом зменшення похибок первинних параметрів. Але із зменшенням похибок первинних параметрів різко зростає вартість апаратури.

Отже, цей шлях можливий, але недоцільний.

2. Зменшення числа первинних параметрів.

Будь-який виріб вимагається виконувати максимально простим. Цей шлях називається методом найкоротшого шляху.

3. Зміна або варіювання коефіцієнтів впливу. Цей метод полягає в оптимізації значень первинних параметрів, а критерієм оптимальності є точність вихідного параметра. Це найбільш ефективний шлях підвищення точності РЕА.

Метод найгіршого випадку (метод максимуму - мінімуму)

Метод базується на визначенні найгірших сполучень похибок первинних параметрів. Нам відома структура об’єкта, склад вхідних параметрів 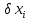, коефіцієнти впливу.

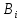Будемо вважати, що з n первинних параметрів k параметрів приймають максимальні значення і мають додатні коефіцієнти впливу, а решта (n - k) – приймають мінімальні значення і мають від’ємні коефіцієнти впливу.

Для спрощення розрахунку при розробці конструкції і технології РЕА використовується оцінка точності за методом найгіршого випадку. Розрахунок виконується для відносних відхилень вхідних і вихідних параметрів РЕА

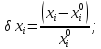
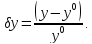
з використанням основного рівняння похибок:

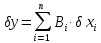
Якщо вважати, що

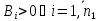
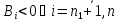
то найгірші відхилення вихідних параметрів з врахуванням виробничих похибок вхідних параметрів визначаються за формулами:

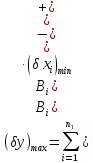
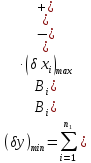
У випадку симетричних відхилень вхідних параметрів

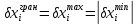
граничне відхилення вихідного параметру

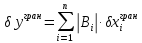
Перевага методу: простота.

Недоліки:

При використанні цього метода приймаємо:

1. відхилення первинних параметрів можуть з великою ймовірністю приймати крайні (гірші) значення, що на практиці, як правило, не спостерігається.

2. Гірші можливі комбінації коефіцієнтів впливу.

3. Таким чином, отриманий найгірший випадок відхилення вихідного параметра дає розширене поле допуску приблизно в 2-10 разів більше реального.

Приклад. Визначити допуск на вихідний параметр.

Коефіцієнти впливу:

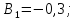
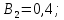
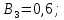
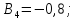
Допуски на вхідні параметри:

Розв’язання

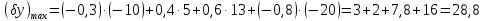
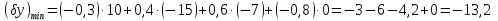
Поле допуску:

%.

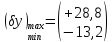Висновок

Ми отримали несиметричне поле допуску, тобто, з’явились фактори, які змістили поле допуску – це четвертий параметр дав найбільше зміщення (16 і 0). За отриманими результатами можна зробити висновок:

• На ширину поля допуску впливають абсолютні значення коефіцієнтів впливу (значення коефіцієнтів впливу за абсолютною величиною).

• На зміщення поля допуску впливає знак коефіцієнта впливу в комбінації з допуском вхідного параметра.

Цей метод може використовуватись як наближений метод аналізу точності вихідних параметрів при невідомих законах розподілу похибок та їх числових характеристик.