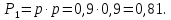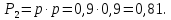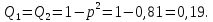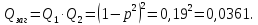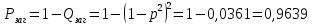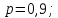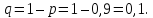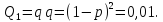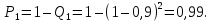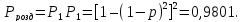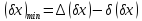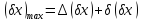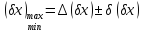- •Основи точності та надійності електронних апаратів частина і. Основи теорії надійності електронних засобів
- •Елементи теорії ймовірності
- •Показники надійності
- •Теоретичні розподіл часу напрацювання до відмови
- •Надійність типових елементів
- •Методи розрахунку надійності
- •Орієнтовні методи розрахунку надійності
- •Уточнений або повний розрахунок надійності
- •Показники довговічності
- •Показники відновлюваності (ремонтопридатності)
- •Комплексний показник надійності
- •Методи забезпечення надійності
- •Конструкторсько-технологічні методи підвищення надійності
- •Класифікація способів резервування
- •Класифікаційна таблиця способів резервування
- •Аналіз надійності системи з загальним постійним резервом
- •Аналіз надійності системи з постійним роздільним резервуванням
- •Частина іі. Основи точності та стабільності функціонування еа
- •Методи аналізу точності функціональних вузлів
- •Імовірнісний метод аналізу точності
- •Експериментальні методи дослідження конструкцій та технологічних процесів
- •Планування експериментів
Класифікаційна таблиця способів резервування

Аналіз надійності системи з загальним постійним резервом
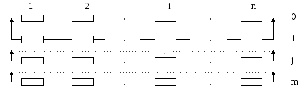
Будемо
вважати, що нам відомі ймовірності
безвідмовної роботи всіх елементів
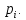 Необхідно
визначити ймовірність безвідмовної
роботи системи в цілому.
Необхідно
визначити ймовірність безвідмовної
роботи системи в цілому.
Визначаємо ймовірність безвідмовної роботи кожної з складових системи.
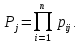
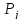 –ймовірності
безвідмовної роботи
–ймовірності
безвідмовної роботи
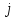 –ї
системи.
–ї
системи.
Переходимо до ймовірності відмов
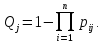
Відмова системи в цілому визначається добутком відмов всіх елементів системи
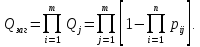
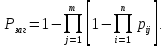
Приклад.
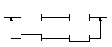
Маємо систему, яка резервована іншою
системою. Ймовірність безвідмовної
роботи всіх елементів однакова
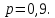 Визначити
ймовірність безвідмовної роботи системи.
Визначити
ймовірність безвідмовної роботи системи.
|
|
|
Надійність підвищилась в 5 – 6 разів.
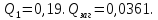
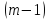 –число
систем, які застосовуються, називається
кратністю
резервування.
Збільшення кратності резервування
приводить до збільшення надійності.
–число
систем, які застосовуються, називається
кратністю
резервування.
Збільшення кратності резервування
приводить до збільшення надійності.
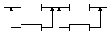
Аналіз надійності системи з постійним роздільним резервуванням
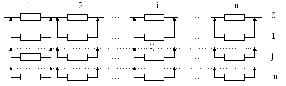
Визначаємо ймовірність безвідмовної роботи групи елементів:
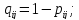
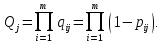
Визначаємо ймовірність безвідмовної роботи узагальненого елемента
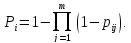
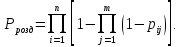
Роздільне резервування більш ефективне.
Приклад.
|
|
|
Ймовірність
відмов
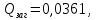 без
резервування
без
резервування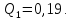
Надійність підвищилась в 10 разів.
Частина іі. Основи точності та стабільності функціонування еа
В основі теорії точності лежить поняття ЕА як складних систем.
Складною системою називається сукупність певних компонентів (складових частин) призначеної для виконання заданої функції.
До властивостей складної системи відносяться:
Ієрархічна підпорядкованість системи та складових частин. Це означає, що будь-який компонент складної системи в свою чергу можна розглядати як складну систему.
Властивість декомпозиції системи. Використовується в задачах аналізу. Будь-яку систему можна розкласти на компоненти.
Властивість композиції системи. Складну систему можна компонувати з компонентів чи складових частин. Композиція використовується для задач синтезу.
Властивість складної системи не може бути простою сумою властивостей окремих компонентів.
Кожна система має певну сукупність функціональних властивостей і функції система може виконувати з тією чи іншою якістю. До якості можна віднести надійність функціонування (довговічність, безвідмовність), точність, стабільність функціонування під дією дестабілізуючих факторів, технологічність, вартість, собівартість, ергономічність (властивість апаратури успішно функціонувати при роботі з людиною), естетичні характеристики РЕА.
Всі параметри, якими характеризується РЕА, як правило, поділяються на дві основні групи: вихідні параметри (вторинні) та вхідні (первинні) параметри.
Якість функціонування РЕА описується вихідними параметрами. Для характеристики властивостей якості використовують параметри, які можна назвати показниками якості.
Тільки той параметр, який відповідає ряду вимог, може називатися показником якості. Зміна параметру повинна приводити до монотонної зміни показника якості.
Показники якості можна назвати вихідними параметрами об’єкта чи системи.
Параметри компонентів, що входять в систему: параметри вхідних сигналів та ряд інших прийнято називати вхідними параметрами.
З такої точки зору систему зручно представляти у вигляді чорної скриньки.
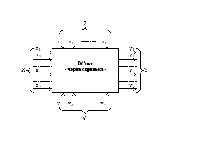
Рис. 1. Модель РЕА у вигляді чорної скриньки
Система
характеризується вектором (множиною)
вхідних параметрів
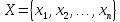 ,
вектором
(множиною)
вихідних параметрів
,
вектором
(множиною)
вихідних параметрів
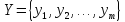 ,вектором
(множиною)
зовнішніх дестабілізуючих факторів
,вектором
(множиною)
зовнішніх дестабілізуючих факторів
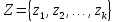 тавектором
(множиною)
зовнішніх керуючих впливів
тавектором
(множиною)
зовнішніх керуючих впливів
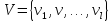 .
.
Така система здійснює перетворення сукупності (вектора) вхідних параметрів в певну сукупність (вектор) вихідних параметрів:
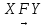 -
символічне зображення,
-
символічне зображення,
де F – перетворення може бути
Функцією
Функціоналом (функція від функції)
Оператором.
Як видно, значення вихідного параметра залежить від первинних параметрів, то між ними має існувати функціональний зв'язок:
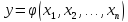
Оскільки в процесі виробництва та експлуатації на первинні параметри діє сукупність різних дестабілізуючих факторів, то первинні параметри будуть представляти собою випадкові величини. Тоді вихідний параметр буде представляти собою функцію від системи випадкових величин і сам по собі також є випадковою величиною. На практиці процес функціонування РЕА описується комплексом вихідних параметрів.
Можна записати систему рівнянь, яка відображає зв'язок між вихідними та вхідними параметрами:
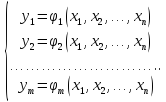
Кожне з рівнянь – це рівняння функціонального зв’язку між вхідними та вихідними параметрами.
Аналітичні методи аналізу точності обов’язково передбачають наявність набору функціональних залежностей.
Похибки параметрів та їх закони розподілу
Похибкою параметра (вихідного або вхідного) називається відхилення значення цього параметра від номінального.
Номінальним називається його розрахункове теоретичне значення.
В результаті дії дестабілізуючих факторів кожних з вхідних і, відповідно, кожних з вихідних параметрів отримують певні відхилення від розрахункових або, інакше кажучи, номінальних значень.
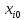 -
розрахункове (номінальне) значення i
– того параметра;
-
розрахункове (номінальне) значення i
– того параметра;
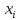 -
діюче значення i
– того параметра.
-
діюче значення i
– того параметра.
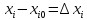 -
абсолютне відхилення ( похибка)
i
– того параметра;
-
абсолютне відхилення ( похибка)
i
– того параметра;
Абсолютна
похибка або абсолютне відхилення
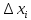 не дає точної (об’єктивної) оцінки
відхилення параметра. Наприклад,
не дає точної (об’єктивної) оцінки
відхилення параметра. Наприклад,
а ± 0,1 – не об’єктивно,
10 ± 0,1 – об’єктивно.
Недоліком абсолютної похибки є те, що вона є розмірною величиною, тобто має розмірність величини, що вимірюється. Тому на практиці використовується відносна похибка або відносне відхилення.
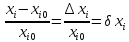
Відносна похибка – це безрозмірна величина виражається у відсотках % і об’єктивно характеризує відхилення параметра незалежно від його номінального значення.
Приклад.
І – й клас точності - ± 5%;
ІІ – й клас точності - ± 10%;
ІІІ – й клас точності - ± 20%;
ІV – й клас точності - + 50% та -20%;
V – й клас точності - + 80% та -20%.
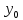 –номінальне
значення вихідного параметра;
–номінальне
значення вихідного параметра;
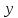 -
біжуче значення вихідного параметра;
-
біжуче значення вихідного параметра;
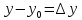 -
абсолютне
відхилення або абсолютна похибка
вихідного параметра;
-
абсолютне
відхилення або абсолютна похибка
вихідного параметра;
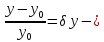 відносне
відхилення або відносна похибка вихідного
параметра;
відносне
відхилення або відносна похибка вихідного
параметра;
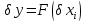 -
похибка
вихідного параметра залежить від похибок
вхідних параметрів.
-
похибка
вихідного параметра залежить від похибок
вхідних параметрів.
Діапазон допустимих відхилень параметра від номінального значення, обмежений верхнім та нижнім граничним відхиленням називається полем допуску на цей параметр. Поле допуску має границі.

(х)min – нижнє граничне відхилення; (х)mах - верхнє граничне відхилення.
(х)min та (х)mах – класичні характеристики поля допуску.
Допуск може бути симетричним і несиметричним із зміщенням вліво або вправо, з одним із граничних відхилень, яке може дорівнювати 0 або виходити за нульове значення.

(x) - координати середини поля допуску;
(x) - половина поля допуску.
|
|
|
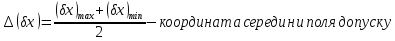
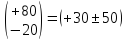
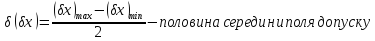
Координату середини поля допуску прийнято називати систематичною похибкою або невипадковою складовою похибки. Половина поля допуску ще називається випадковою складовою похибки.
В межах поля допуску похибки мають визначені закони розподілу.
Класифікація похибок параметрів
Похибки вхідних параметрів виникають внаслідок дії тих чи інших дестабілізуючих факторів, які можуть проявлятися і в процесі виробництва і в процесі експлуатації РЕА.
Похибки, які виникають в процесі виробництва РЕА, називаються виробничими. Виробничі похибки визначають точність функціонування РЕА.
Похибки, які виникають в процесі експлуатації РЕА, називаються експлуатаційними. Їх називають по виду того фактору, який викликає цю похибку (температурні, старіння, похибки, викликані дією підвищеної вологості).
Закони розподілу та числові характеристики похибок параметрів
В ідеальному випадку, тобто коли забезпечено стабільність технологічних процесів, закони розподілу як виробничих, так і експлуатаційних похибок, є нормальними:
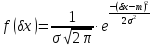
m = mx – математичне сподівання похибки x (або Мx);
= х = х - середнє квадратичне відхилення.
Нормальний закон симетричний.
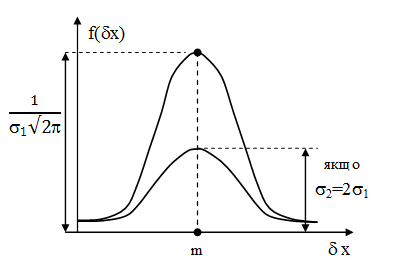
Нормальний закон розподілу формується згідно з центральною граничною теоремою теорії ймовірності:
Розглядається N випадкових величин з довільними законами розподілу, але з обмеженою зверху дисперсією. Якщо N , то закон розподілу суми цих величин буде наближатися до нормального.
Виробничі похибки
Виробничі похибки виникають в процесі виробництва РЕА внаслідок нестабільності технологічних процесів, неоднорідністю вихідних матеріалів, неточністю обладнання або інструменту, іншими суб’єктивними факторами (помилки людини-оператора, зовнішніми умовами, що змінюються).
Умовами виникнення нормального закону розподілу виробничих похибок є:
кількість випадкових факторів, які діють в конкретному технологічному процесі, повинна бути достатньо великою (7 – 10 факторів);
серед факторів не повинно бути домінуючих (тобто дисперсії повинні бути однаковими):
дестабілізуючи виробничі фактори повинні бути стабільними в часі на протязі тривалого періоду.
Основні числові характеристики закону розподілу похибок.
1. При розв’язанні багатьох практичних задач, пов’язаних з аналізом технологічних процесів, немає потреби повністю характеризувати сукупність. Можна використати показники, які характеризують сукупність у цілому і закономірності, властиві їй, але з певної сторони. Такими показниками є статистичні характеристики, які визначають на основі розгляду варіантів і їх частот при отриманні варіаційного ряду.
Найважливішими характеристиками будуть:
характеристики розташування;
характеристики розсіювання параметра;
характеристика форми кривої розподілу.
Характеристики розташування.Розташування кривої розподілу визначають тим її значенням, відносно якого розташовані всі інші значення параметра. До характеристик розташування кривої розподілу відносятьсереднє арифметичне значення або математичне сподівання.
Середнє арифметичне значення варіаційного ряду– сума добутків усіх варіантів на частоти (частості), що відповідають їм, поділена на суму частот
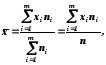
де хі–і-е значення параметра;ni– частота (частість) появиі-го значення параметра;m– кількість варіантів значень параметра.
Як характеристика розташування середнє значення є центром, відносно якого групуються окремі значення параметра.
Для середнього арифметичного значення характерні наступні властивості:
- якщо всі варіанти збільшити (зменшити) в одне і теж число (або на одне і теж число) разів, то середнє арифметичне значення збільшиться (зменшиться) у стільки ж разів;
- сума добутків відхилень варіантів від їх середнього арифметичного значення на ваги, що їм відповідають, дорівнює нулю;
- середнє арифметичне значення суми (різниці) дорівнює сумі (різниці) середніх арифметичних.
При наближенні обсягу сукупності до нескінченності (n ) частотиniнаближаються (сходяться по ймовірності) до відповідних ймовірностейрі. Таким чином, середнє арифметичне значення при збільшенніn (n )буде наближатися (сходитись по ймовірності) до його математичного сподівання:
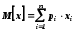 для дискретного
ряду;
для дискретного
ряду;
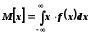 для інтервального
ряду,
для інтервального
ряду,
де рі– ймовірністьі-го значення параметра;
n – обсяг сукупності;
хі –і-те значення параметра;
f(х)– густина розподілу параметра.
Середнє арифметичне значення змінюється із зміною будь-якого варіанта. Воно особливо чутливе до зміни крайніх варіантів.
Характеристики розсіювання параметра. Вони відображають розсіювання параметра відносно деякого значення, наприклад, середнього арифметичного значення. Чим більша змінюваність параметра, тим більше розсіяна крива розподілу по осі абсцис. Для кількісної оцінки степені розсіювання параметра служить дисперсія.
Дисперсія– це середнє арифметичне значення квадратів відхилень варіантів від їх середньоарифметичної величини
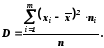
Для характеристики розсіювання часто зручніше мати величину, яку виражають у тих же одиницях, що і значення параметра. Таким показником є середньоквадратичне відхилення
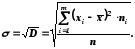
Середньоквадратичне відхилення є також показником однорідності даної сукупності. Мале значення середньоквадратичного відхилення свідчить про те, що середня арифметична величина добре відображає в собі представлену сукупність.
Дисперсії характерні наступні властивості:
якщо всі варіанти збільшити (зменшити) в одне і теж число, наприклад, Сразів, то дисперсія збільшиться (зменшиться) уС2разів;
зменшення (збільшення) варіантів на одну і ту саму постійну величину не змінює значення дисперсії;
дисперсія відносно середньоарифметичної величини мінус квадрат різниці між середнім арифметичним і цією постійною
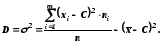
При спрямуванні обсягу сукупності до нескінченності (n )частотиniнаближаються (сходяться по ймовірності) до відповідних значень ймовірностірі, а середнє арифметичне значення – до математичного сподіванняM[x]
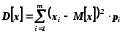 - для дискретного
ряду;
- для дискретного
ряду;
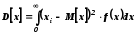 - для інтервального
ряду.
- для інтервального
ряду.
Характеристики форми кривої.Про форму кривої несе інформацію її скіс (асиметричність) і крутизна.
Скіс називають додатнім, якщо гілка кривої розподілу, починаючи від вершини, буде більша лівої. Скіс називаютьвід’ємним, якщо ліва гілка кривої розподілу, починаючи від вершини, буде більша правої.
Мірою скосу є асиметрія
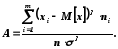
У симетричного розподілу А=0. У рядів з додатною косістю А>0; у рядів із від’ємною косістю – А<0. Поява асиметричності у кривої розподілу може говорити про різнотипний склад сукупності.
Крутість кривої розподілу говорить про відміну даної кривої від нормальної за концентрацією окремих значень навколо центру розподілу. Крутість ряду розподілу, в якому значення тільки трьох одиниць з 1000 лежить поза границями 3, називаютьнормальною крутістю. При накопиченні значень навколо середнього значення в більшій кількості в порівнянні з нормальною, крутість називаютьдодатною. В цьому випадку крива має гостру вершину. Це явище називаютьексцес.
При накопиченні значень навколо середнього значення в меншій кількості в порівнянні з нормальною, крутість називають від’ємною. Ця крива має плоску вершину, а явище називаютьдефектом.
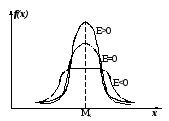
Крива густини ймовірності з від’ємним (Е0),
нульовим (Е=0) та додатнім значенням ексцесу (Е0)
Показник крутості визначають за формулою
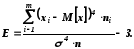
Ця формула підібрана таким чином, щоб для гостровершинної кривої Е> 0, а для плосковершинної –Е< 0.
Кожен технологічний процес при його дослідженні у звичайних для нього умовах дає певному параметру типову для нього криву розподілу. Усяка зміна форми кривої розподілу, її параметрів говорить про порушення або зміни в умовах його реалізації.
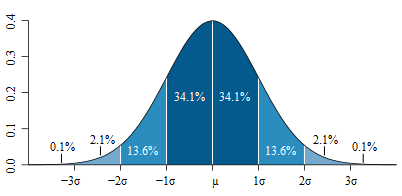
Правило
3.
В
межах ±3
знаходиться 0,9973 всіх значень випадкової
величини. Тобто,
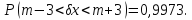
У
сучасних технологіях використовується
правило
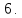 Значення
Значення
 є в 2 рази менше, ніж при використанні
правила
є в 2 рази менше, ніж при використанні
правила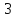 ,
тоді ймовірність
,
тоді ймовірність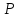 є вище, ніж при
є вище, ніж при