3. Розробка алгоритму програми

Основна задача розробки алгоритму програми це вибір або адаптація відповідного існуючого алгоритму для рішення поставленої задачі. Завжди існують альтернативні рішення і вибір кращого з них залежить від знань про те, як ці рішення будуть поводитися при зростанні розміру вхідних даних. Розробці алгоритмів присвячено окремі підручники, наукові роботи і окремі навчальні курси. В даній лабораторній роботі будуть розглядатися тільки окремі важливі питання розробки алгоритмів обробки природної мови.

Найбільш відома стратегія розробки алгоритмів це divide-and-conquer (Поділяйі володарюй). Якщо потрібно вирішити задачу (проблему) розміромn, то можна її поділити на дві проблеми розмірами n/2, вирішити ці проблеми і поєднати ці результати для рішення початкової задачі (проблеми). Наприклад, припустимо, що потрібно відсортувати слова записані на окремих картках. Таке сортування можна виконати віддавши одну половину карток одній людині а іншу другій, які будуть сортувати тільки свої картки (звичайно вони можуть поступити аналогічно). Дві частини вже відсортованих карток не складно об’єднати в одне ціле. Рисунок 2 ілюструє такий підхід до вирішення задачі сортування.

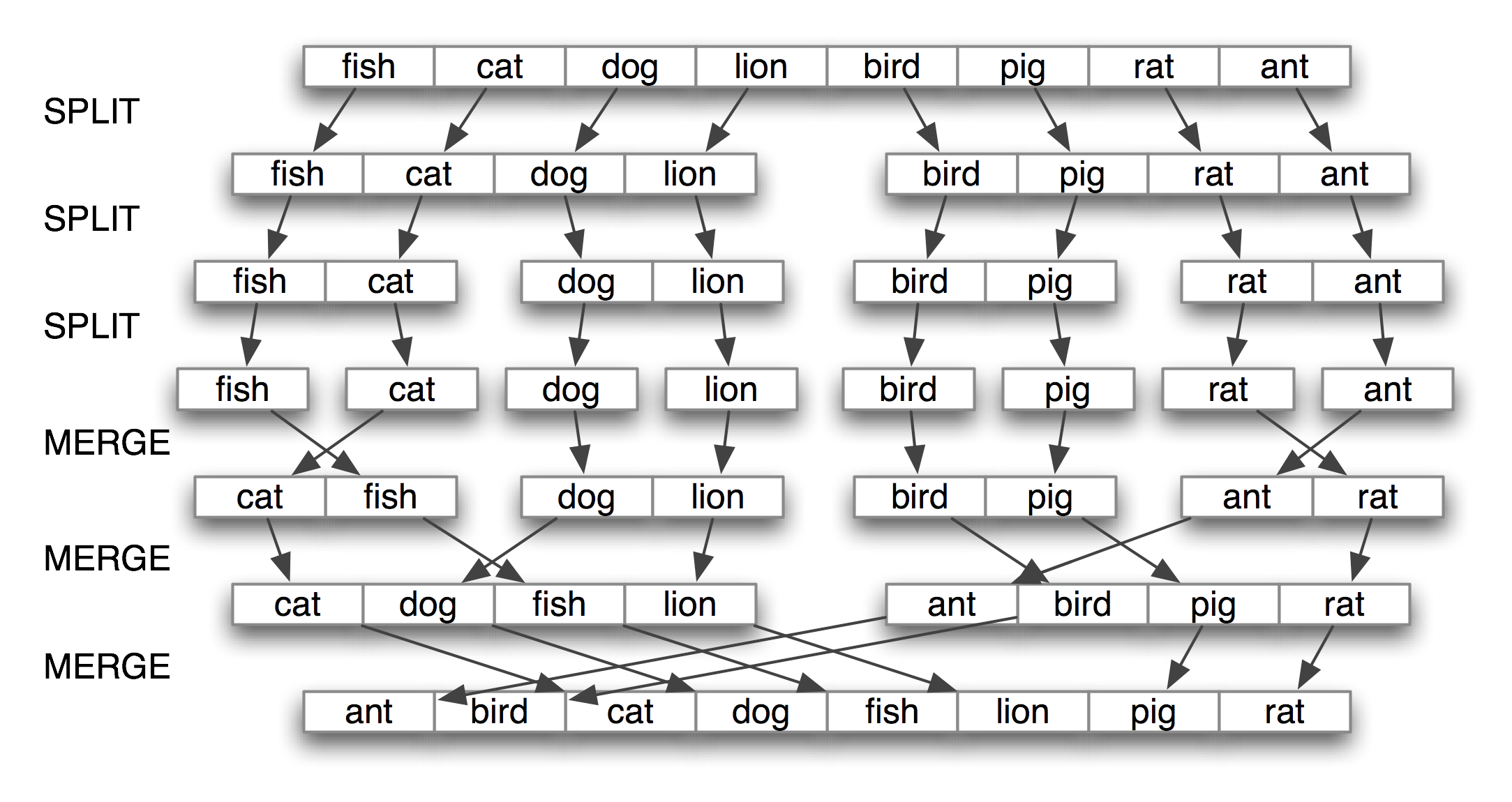
Рис. 2 Сортування на основі Divide-and-Conquer.

Іншим прикладом може бути пошук слова у словнику. Книжка (словник) відкривається посередні і слово порівнюється з словами на цій сторінці. Якщо виявиться, що слово повинно бути в першій половині словника то знову перша половина ділиться, приблизно, на дві ріні частини і пошук повторюється. Такий метод пошуку називається бінарним пошуком, під час якого проблема ділиться на дві половини на кожному кроці.

Інший підхід до розробки алгоритму це перетворення проблеми до проблеми рішення якої вже відоме. Наприклад, для визначення дублювання елементів в списку, можна спочатку здійснити попереднє сортування списку, а потім перевірити чи не є сусідні пари елементи ідентичними.

3.1 Рекурсія

Приклади сортування та пошуку мають вражаючу властивість: для рішення проблеми розміром n, ця проблема ділиться на на дві половини і тоді вирішується одна або більше проблем розміромn/2. Загальний спосіб реалізувати такі методи це використати рекурсію. Визначається функція, яка спрощує проблему і ця функція викликає саму себе для рішення одного або більше випадків тієї самої проблеми. Далі ці результати поєднуються в рішенні початкової проблеми.

Наприклад, припустимо, що маючи набір зn слів, потрібно визначити скільки існує різних комбінацій поєднання цих слів у послідовність. Якщо є тільки одне слово (n=1), то існує тільки одина комбінація побудувати на основі цього слова послідовність. Якщо є два слова, то можливі дві різні комбінації цих слів. Для трьох слів існує шість комбінацій. В загальному, для n слів, можливі n × n-1 × … × 2 × 1 комбінації(факторіалn). Запрограмувати обчислення цього факторіалу можна наступним чином:

>>> def factorial1(n): ... result = 1 ... for i in range(n): ... result *= (i+1) ... return result

Звичайно, існує також рекурсивний алгоритм рішення цієї задачі на основі наступних спостережень. Нехай, потрібно побудувати всі можливі комбінації зn-1 окремих слів. Для кожної такої комбінації існуєnпозицій куди можна вставити нове слово: на початок, в кінець, або в n-2 проміжків між словами. Таким чином потрібно просто перемножити кількість рішень знайдених дляn-1 на значення n. Необхідно також визначити початкову умову, яка говорить що для одного слова можлива тільки єдина комбінація. Запропоноване рішення можна запрограмувати наступним чином:

>>> def factorial2(n): ... if n == 1: ... return 1 ... else: ... return n * factorial2(n-1)

Два алгоритми вирішують ту саму задачу. Перший використовує ітерації а другий рекурсію. Рекурсію зручно використовувати для керування вкладеними об’єктами, наприклад, такими як ієрархія гіпернімів вWordNet. Спробуємо обчислити кількість гіпернімів в ієрархії починаючи від кореня – заданого синсетуs. Для вирішення цієї задачі потрібно знаходити кількість всіх гіпонімів s, та додавати їх (також потрібно безпосередньо для синсету додати1). Наступна функціяsize1() дозволяє виконати такі обчислення. В функції використовується рекурсивний викликsize1():

>>> def size1(s): ... return 1 + sum(size1(child) for child in s.hyponyms())

Також можна розробити рішення цієї задачі на основі здійснення ітерацій по рівнях в ієрархії. Перший рівень, це власне сам синсет #1, наступний – всі гіпоніми синсету, далі всі гіпоніми гіпонімів. На кожному кроці циклу визначається кількість гіпонімів на попередньому рівні#2і формується наступний набір гіпонімів наступного рівня#3.

>>> def size2(s): ... layer = [s] #1 ... total = 0 ... while layer: ... total += len(layer) #2 ... layer = [h for c in layer for h in c.hyponyms()] #3 ... return total

Друге рішення є те тільки довшим але і складнішим для розуміння. Потрібно думати процедурно і слідкувати за зміною змінних layer та total на всіх кроках алгоритму. Для того щоб пересвідчитися, що два рішення дають однакові результати спробуємо визначити кількість гіпернімів в ієрархії починаючи з першого значення словаdog:

>>> from nltk.corpus import wordnet as wn >>> dog = wn.synset('dog.n.01') >>> size1(dog) 190 >>> size2(dog) 190