Фізико-технічні параметри ексимерного - лазера

Параметр	- лазер
Довжина хвилі, нм	248
Режим роботи	імпульсний
Тиск газу, Па	(1–6)105
Метод накачки	розряд, керований електронним пучком	самостійний газовий розряд
Енергія в імпульсі, Дж	0,1–350	0,1–1
Тривалість імпульсу, нс	20–103	15–30
Частота повторення імпульсів, Гц	окремі	103
Середня потужність, Вт	150	100
ККД, %	10	1

Газорозрядний спосіб збудження дозволяє реалізовувати також імпульсно-періодичний режим генерації ексимерних лазерів. Досягнута в теперішній час частота імпульсів становить 10²...10³ Гц при середній потужності випромінювання 10–100 Вт і ККД – 1 %.

Порогове значення інверсії для ексимерних лазерів досить велике. Це зумовлено короткохвильовим діапазоном їх випромінювання та широкою лінією підсилення активної речовини. Вираз для коефіцієнта підсилення у випадку, коли в нижньому стані молекули відсутні, має вигляд

де N_B – густина молекул у верхньому стані; ∆ν – ширина лінії підсилення; А₂₁ – ймовірність спонтанного випромінювання; λ – довжина хвилі. Для ексимерних лазерів А₂₁=10⁷–10⁸с^-1; λ = (2–3)10^-5 см, тому, задаючи порогове значення підсилення χ=10^-2, побачимо, що здійснення генерації потребує достатньо високої концентрації ексимерних молекул N_B =10¹⁴–10¹⁵ см^-3. Для створення потрібної густини збудження молекул потрібно забезпечити відповідне значення густини енергії накачування ρ = 10^-2 Дж/см³ за час 10^-8 –10^-7с.

2. Розрахунок просторових та спектральних характеристик газових лазерів

Дані для розрахунку: радіуси кривизни дзеркал R₁, R₂, довжина хвилі випромінювання , довжина резонатора L (рис. 2).

Рис.2. Функціональні схема активного резонатора: 1 – дзеркала резонатора; 2 – кювета з активною речовиною; р₁, р₂ – відстань від краю кювети до поверхні дзеркала; d_к – діаметр кювети; 2а – діаметр дзеркала; R₁, R₂ – радіуси кривизни дзеркал

Вибір конфігурації резонатора. В нашому випадку довжина резонатора практично була задана і завдання вибору полягає у визначенні необхідних радіусів використаних дзеркал. На практиці на вибір резонатора впливає також конструкція лазера. З одного боку вигідно працювати на квазіплоских резонаторах, які забезпечують максимальний відбір потужності та мінімальне розходження пучка випромінювання. Однак такі резонатори критичні до роз’юстування, тому можливість їх використання визначається жорсткістю конструкції, її стійкістю до механокліматичного впливу. Найбільшу стійкість до роз’юстування має конфокальний резонатор, однак він характеризується малим об’ємом моди, а значить пониженим відбором генерованої потужності. Конфокальний резонатор також чутливий до довжин резонатора.

В результаті на практиці працюють з резонаторами, середніми між квазіплоскими та конфокальними.

Стійкі резонатори з круглими дзеркалами. Резонатор, який відповідає умові стійкості (0g₁g₂1) називається стійким. Тип резонатора та його властивості визначаються параметрами:

де а₁, а₂ – радіуси дзеркал; g₁, g₂ – узагальнені параметри резонатора; N_ф1, N_ф2 – числа Френеля; R₁, R₂ – радіуси кривизни дзеркал (рис.3).

Рис.3. Діаграма стійкості резонатора (R – радіус кривизни дзеркала)

У цьому разі маємо:

g₁=g₂=1 – стійкий резонатор із плоскими дзеркалами;

g₁=g₂=0 – стійкий конфокальний резонатор із двома однаковими вгнутими дзеркалами;

g₁=g₂= –1 – стійкий концентричний резонатор із двома однаковими вгнутими дзеркалами, за структурою відповідає випадку g₁=g₂=1.

Крім цього, справедливими є умови:

0<g₁g₂<1 (стійкий резонатор для випадку N_i>50 (i=1, 2), який можна розглядати в наближенні геометричної оптики; дифракційні втрати зростають, коли N_i<50 і визначають властивості резонатора);

1–g₁g₂<0 (нестійкий резонатор, електромагнітна хвиля вже після кількох відбивань не потрапляє на дзеркало).

Не варто також використовувати резонатори з g₁g₂=0 або g₁g₂=1, оскільки роз’юстування легко приводить у нестійку область. Хорошу стабільність щодо роз’юстування мають резонатори з g₁g₂=1/2.

Стійкі резонатори з двома ввігнутими дзеркалами різних радіусів кривизни.

Розраховуємо узагальнені параметри резонатора (рис.4):

,

.

Рис.4. Схема резонатора з двома ввігнутими дзеркалами різних радіусів кривизни: z₀ – зміщення “перетяжки” від центра резонатора; W₀ – радіус “перетяжки”; W(z)– радіус світлової плями на поверхні дзеркала; L – довжина резонатора; R₁, R₂ – радіуси кривизни дзеркал

Визначаємо величину зміщення перетяжки Z₀ від центра резонатора, для чого визначаємо спочатку параметри іu:

Визначаємо мінімальний розмір каустики (розмір перетяжки) 2W₀, визначивши спочатку параметр R_екв:

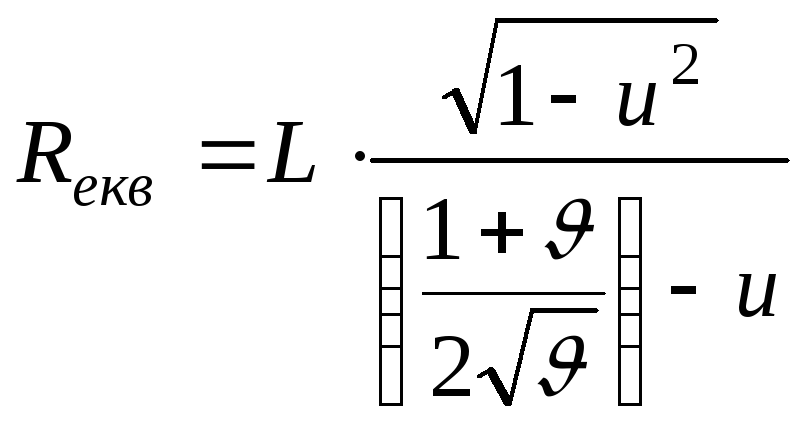
, де , тоді

Знаходимо розміри світлової плями на обох дзеркалах резонатора 2W₁(z) і 2W₂(z):

Визначаємо діаметр газорозрядного капіляра (кювети), якщо W₁(z)>W₂(z), то:

,

а радіус дзеркала .

Відповідно до умови самозбудження лазера, коефіцієнт квантового підсилення на порозі генерації повинен дорівнювати сумарним втратам. Сумарні втрати складаються з втрат на дзеркалах, втрат на дифракцію та втрат на розсіювання світла на неоднорідностях активного середовища. Цю умову можна записати так:

G=_;

_=_розс+_дзер+_диф;

_дзер = .

де L – довжина резонатора; r₁, r₂ – коефіцієнти відбиття «глухого» та напівпрозорого дзеркал відповідно.

_диф = ,

де –це (m+1)–й корінь функції Бесселя першого роду п–го порядку; N_ф – число Френеля.

У табл. 4 наведено значення коефіцієнтів при для деяких індексівт і п.

Таблиця 4.

т	п=0	п=1	п=2	п=3	п=4
0	0,300	0,767	1,38	2,13	3,00
1	1,59	2,57	3,70	4,98	6,40
2	3,92	5,40	7,05	7,05	10,80
3	7,28	9,30	11,40	11,40	16,25
4	11,65	14,20	16,90	19,70	22,60

Конфокальний стійкий резонатор, властивості якого переважно визначаються дифракцією.

Для дифракційних втрат, коли число Френеля N_ф>1 дійсним є співвідношення

Найменший поперечний переріз пучка лежить посередині резонатора та має радіус:

У місці розміщення дзеркала радіус лазерного пучка дорівнює:

Для повного формування мод необхідно, щоб радіус дзеркал а був більшим за радіус лазерного променя в місці їх розташування.

Сумарний кут розходження пучка в дальній зоні (визначений на рівні половинної інтенсивності для моди ТЕМ₀₀) дорівнює:

Стійкий резонатор із плоским і сферичним дзеркалами. “Перетяжка” пучка лежить на плоскому дзеркалі (рис. 5) і має радіус

Радіус пучка на вгнутому дзеркалі дорівнює:

Сумарний кут розходження пучка становить:

Рис.5. Схема резонатора з плоским і сферичним дзеркалами: W₀ – радіус “перетяжки”; W(z)– радіус світлової плями на поверхні дзеркала; L – довжина резонатора; R₁, R₂ – радіуси кривизни дзеркал

Стійкий резонатор із двома різними або також із двома однаковими вгнутими дзеркалами, властивості якого визначаються дифракцією.

Для резонансних частот маємо:

Найменший поперечний переріз пучка міститься на відстані t від дзеркала 1, причому t вважається додатним у напрямку до дзеркала 2 резонатора. Якщо t від’ємне, то найменший поперечний переріз пучка перебуває на відстані t від дзеркала 1 зовні резонатора. Маємо:

Радіус “перетяжки” (визначається як радіус, де інтенсивність моди ТЕМ₀₀ спадає до е^-2 максимального значення на осі резонатора) визначається з виразу:

Радіус пучка на дзеркалах становить:

Кут розходження пучка в дальній зоні для моди ТЕМ₀₀ дорівнює:

Розрахунок спектральних характеристик резонатора.

Знаходимо частоту ₀ – центральну частоту лінії підсилення робочого переходу (рис.6):

.

Рис.6. Спектр активного резонатора: 1,2,4 – моди резонатора; 3 – контур лінії підсилення робочого переходу; _д – допплерівська ширина лінії; _р – ширина спектральної лінії резонатора; ₀ – центральна частота;  – відстань між двома сусідніми частотами для аксіальних типів коливань: _ – сумарні втрати в резонаторі

Розраховуємо сумарні втрати:

_=_розс+_дзер+_диф;

Розраховуємо ширину спектральної лінії резонатора _р, враховуючи сумарні втрати _:

Знаходимо відстань між сусідніми частотами резонатора  для аксіальних мод:

Знаходимо ширину спектральної лінії випромінювання лазера _N (рис.7.):

Рис.7. Формування спектральних ліній випромінювання лазера: 1 – моди резонатора; 2 – лінії підсилення робочого переходу;_N – ширина спектральної лінії випромінювання лазера; ТЕМ_00q – аксіальні моди резонатора

Розраховуємо допплерівську ширину лінії підсилення _D

де Т – температура (К), М – молекулярна маса газу (кг).

Розраховуємо гауссівський контур лінії підсилення:

.

Розраховуємо частотний спектр резонатора для багатомодового режиму.

Для резонатора з двома плоскими дзеркалами спектр власних коливань задається виразом:

де L – довжина резонатора, т, п, q – цілі числа.

Для конфокального резонатора спектр резонансних частот записується у вигляді:

Для резонансних частот резонатора, в якому одне дзеркало плоске, а друге сферичне, маємо:

Розраховуємо коефіцієнт підсилення активного середовища.