Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный университет Львовская политехника

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Множини остаточний вар_ант.doc

Скачиваний:

146

Добавлен:

12.02.2016

Размер:

1.83 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 64 5 6 > Следующая >>>

7. Комп’ютерне представлення множин

Зобразити множини у комп’ютері можна різними способами. Наприклад, накопичити елементи множини в невпорядкованому вигляді. Але тоді операції із множинами вимагатимуть значних ресурсів часу, адже щоразу необхідно буде здійснювати перегляд елементів. Тому є інші способи зображення множин у комп'ютері.

Одним із найпоширеніших та найпростіших способів є зображення множин за допомогою бітових рядків. Нехай універсальна множина U містить п елементів. Упорядкуємо довільним способом елементи універсальної множини. Тоді

Множину зображають у комп'ютері рядком із 0 та 1 довжинип так: якщо , то і-й біт дорівнює 1, якщо , то і-й біт дорівнює 0.

Приклад 7.1. Нехай ,,. Тоді множину A зобразимо рядком 010000110110, а множину В – рядком 110001100100. _

Після представлення множин у вигляді бітових рядків, легко робити операції над ними, адже це будуть порозрядні логічні операції над відповідними рядками.

Наприклад, перетин множин – це порозрядна кон'юнкція над бітовими рядками, а об'єднання множин – порозрядна диз'юнкція над бітовими рядками.

Логічні операції наведені в табл. 7.1.

Таблиця 7.1.

а_i	b_i
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	1

Приклад 7.2. Нехай ,,. Знайдемо комп'ютерне зображення перетину множин . Виконаємо порозрядну кон'юнкцію рядків, які зображають множини А та В:

= 010000110110;

= 110001100100.

= 010000100100.

Отже, повертаючись до звичайного зображення множин, маємо ._

Приклад 7.3. Нехай ,,. Знайдемо об'єднання множин . Виконаємо порозрядну диз'юнкцію рядків, які зображають множини А та В:

= 010000110110;

= 110001100100;

= 110001110110.

Отже, ._

Якщо універсальна множина U має велику потужність, а підмножини універсальної множини не дуже потужні, то зображення за допомогою бітових рядків не є ефективним з точки зору витрат пам'яті. У такому разі для зображення множин доцільно використовувати інші структури даних – як правило, зв'язані списки, масиви або хеш-таблиці.

8. Приклади розв’язування завдань

Приклад 8.1. Задати двома різними способами множину А всіх парних чисел 2, 4, 6, ...., що не перевищують 1000.

Розв’язання:

Перерахуванням: А={2, 4, 6, 8, 10, …, 998, 1000};
Описом: А={(x|xN)(х/2N), N1000}; (N – множина натуральних чисел 1, 2, 3, ….).▲

Приклад 8.2. Зобразіть фігури, задані множинами ,, де– дійсна площина. Які фігури зображають множини?

Розв’язання:

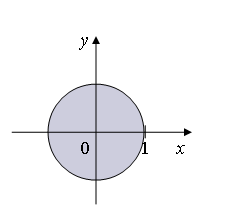
Множина А Множина В

Множина Множина

Множина

Приклад 8.3. Чи правильні рівності:

1) {{1,2}, {2,3}}={1,2,3}?

2) {{1,2}}={1,2}?

Розв’язання:

1) Ні, адже елементами першої множини є підмножини {1,2} та {2,3}, а другої – елементи 1,2,3.

2) Ні, тому що перша множина одноелементна, тобто складається з одного елемента – підмножини {1,2}, а друга має два елементи 1 та 2. ▲

Приклад 8.4. Перечисліть елементи наступних множин:

1) А={a|aB, B={1,2,3}};

2) A={a|aB, B={1,2,3}}.

Розв’язання:

1) Так, як аВ, а В – трьохелементна множина, то існує 2³=8 підмножин: А={{1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}, }.

2) Так, як аВ, то А=В={1,2,3}.▲

Приклад 8.5. Довести, використовуючи закони алгебри множин, що

Розв’язання:

▲

Приклад 8.6. Спростити вираз

Розв’язання:

Використовуючи закони алгебри множин:

▲

Приклад 8.7. Опитування 100 студентів показало, що серед них англійську мову вивчають 29 студентів, німецьку – 30, французьку – 9, лише французьку – 1, англійську та німецьку – 10, німецьку та французьку – 4, всі три мови – 3 студенти. Скільки студентів не вивчають жодної мови? Скільки студентів вивчають лише німецьку мову? У розв’язку використовувати діаграми Ейлера-Венна.

Розв’язання:

Введемо позначення:

U – множина всіх опитаних студентів;

А – множина студентів, які вивчають англійську мову;

Н – множина студентів, які вивчають німецьку мову;

Ф – множина студентів, які вивчають англійську мову.

З умови задачі очевидно, що =3, тоді=4-3=1;10-3=7. У такому випадку лише німецьку мову вивчають 30-7-3-1=19 студентів.

Із умови задачі також випливає, що 9-1-1-3=4, тому лише англійську мову вивчають 29-4-3-7=15 студентів. Тоді число студентів, що не вивчають жодної мови, буде рівним100-(1+1+3+4+7+15+19)=50 студентів.

Рис. 8.1 Діаграма Ейлера-Венна

Приклад 8.8. Довести, що для будь-яких множин А та В виконується рівність .

Розв’язання:

Для доведення використаємо метод від супротивного, тобто нехай і.

Із АВ випливає, що якщо аА, то аВ. (1)

З іншої сторони із існує такий елемента, що та, отжеі. (2)

Використовуючи (1) та (2):

З того, що івипливає, щота, а звідси=, тобто отримали суперечність.

Таким чином, вираз хибний і тому, тобто.

Аналогічно можна показати, що і, отже,, що і потрібно було довести. ▲

Приклад 8.9. Знайти декартовий добуток множин A={1,2,3}, B={a,b} та його потужність.

Розв’язання:

AB = {(1,a), (1,b), (2,a), (2,b), (3,a), (3,b) },

BA = {(a,1), (a,2), (a,3), (b,1), (b,2), (b,3) }.

Як бачимо, AB  BA.

Потужність декартового добутку: |AB|=|BA| = 32=6. ▲

Приклад 8.10. Довести рівність множин: (B)С=(AC)(BC)

Розв’язання:

Доведемо, що (B)С(AC)(BC).

Нехай z(AB)С, тоді z=(x,y), де xAB та yС. Отже, xA або xВ. Тобто xA та yС або xВ та yС. Тому zAC або zBC. За означенням об’єднання z(AC)(BC).

Доведемо, що (B)С(AC)(BC).

Нехай z(AC)(BC), тоді zAC або zBC. Так як z=(x,y), то xA, yС або xB, yС.Отже, xA або xВ при yС. Тому xAB і yС. За означенням декартового добутку z(B)С. ▲

Приклад 8.11. Зобразіть на координатній площині декартовий добуток множин А×В, якщо:

А= {1,2,3}, В=[3,5];
А={х ׀ xR, 1≤x≤3}; B={y ׀ yR, 3≤y≤5};
А=R, В=[3,5];
А=R, В=R.

Розв’язання:

а) Так як множина А складається з трьох елементів, а множина В містить всі дійсні числа від 3 до 5, включаючи і самі ці числа, то декартовий добуток А×В складатиметься з нескінченної кількості пар, перша компонента яких або 1, або 2, або 3, а друга – будь-яке дійсне число з проміжку [3, 5]. Безліч таких пар дійсних чисел на координатній площині зобразиться трьома відрізками (рис. 8.2).

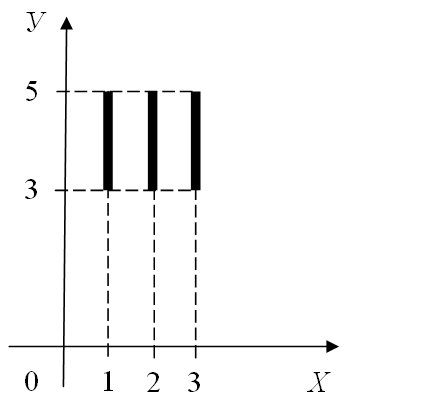
Рис. 8.2.

b) У цьому випадку нескінченними є обидві множини А і В. Тому першою координатою пари, що належить множині А×В, може бути будь-яке число з проміжку [1, 3], а другою – будь-яке число з проміжку [3,5] і, отже, точки, що зображують елементи декартового добутку даних множин А і В, утворюють квадрат (рис. 8.3).

Рис. 8.3.

с) Цей випадок відрізняється від попереднього тим, що множина А складається з усіх дійсних чисел, тобто абсциса точок, що зображають елементи множини А×В, приймає всі дійсні значення, в той час як ордината вибирається з проміжку [3, 5].

Безліч таких точок утворює нескінченну смугу (рис. 8.4).

Рис. 8.4.

d) Декартовий добуток R×R складається з різноманітних дійсних чисел. Точки, що зображують ці пари, суцільно заповнюють координатну площину.

Таким чином, декартовий добуток R×R містить стільки ж елементів, скільки точок знаходиться на координатній площині. ▲

Приклад 8.12. На координатній площині побудувати множину (-1; 3×1; 3).

Розв’язання:

Першу множину поміщаємо на осі OX, другу на осі OY. Множина всіх пар, тобто декартовий добуток, зображається точками заштрихованого прямокутника, але без лівої та нижньої сторони (рис. 8.5).

Рис. 8.5 Декартовий добуток

Приклад 8.13. Скільки цілих чисел між 0 та 1000 містять рівно одну цифру 6?

Розв’язання:

Нехай S – множина цілих чисел між 0 та 1000, що містять рівно одну цифру 6. Розглянемо три підмножини S₁, S₂ та S₃ множини S.

S₁ – множина, яка містить число, що складається з однієї цифри і ця цифра 6;

S₂ – множина, яка містить двохзначне число, що містить лише одну цифру, яка рівна 6;

S₃ – множина, яка містить трьохзначне число, що містить лише одну цифру, яка рівна 6.

Множина S₁ містить лише один елемент – число 6.Отже,  S₁=1.

У множині S₂ кожен елемент, що містить 6, є або першою, або другою цифрою. Якщо 6 – друга цифра, то існує 8 різних чисел, які будуть стояти на першій позиції, оскільки перше число не може бути 0 або 6. Якщо 6 – перша цифра, то таких чисел 9, оскільки друга цифра не може бути рівна 6. Таким чином, S₂ містить 8+9=17 елементів, тобто  S₂=17.

Елемент із S₃ може містити 6 як першою, так і другою чи третьою цифрою. Якщо 6 – перша цифра, то існує 9 варіантів вибору другої цифри та 9 варіантів вибору третьої цифри. Згідно комбінаторному принципу множення, S₃ містить 9 9=81 чисел з першою цифрою 6. Якщо 6 –друга цифра, то існує 9 варіантів вибору третьої цифри та 8 варіантів вибору першої цифри, оскільки перша цифра не може бути нулем. Очевидно, S₃ містить 98=72 чисел, у яких 6 – друга цифра. Аналогічно, S₃ містить 72 числа, у яких 6 – третя цифра. Отже, всього S₃ містить 81+72+72=225 елементів, тобто S₃=225.

Оскільки та множиниS₁, S₂ і S₃ – ті, що попарно не перетинаються, тоді

.▲

Приклад 8.14. Скільки додатних цілих чисел, менших 1001, діляться на 2, 3 чи 5?

Розв’язання:

Нехай X – множина додатних цілих чисел, які діляться на 2, 3 чи 5. Розглянемо три підмножини X₁, X₂ і X₃ множини X.

X₁ – множина додатних цілих чисел, які діляться на 2. Число елементів чи потужність цієї множини дорівнює .

X₂ – множина додатних цілих чисел, які діляться на 3 Число елементів чи потужність цієї множини дорівнює .

X₃ – множина додатних цілих чисел, які діляться на 5. Число елементів чи потужність цієї множини дорівнює .

Тоді множина X₁X₂ – множина додатних цілих чисел, які діляться на 2 або 3. Відповідно . МножинаX₁X₃ – множина додатних цілих чисел, які діляться на 2 або 5. Тоді . МножинаX₂X₃ – множина додатних цілих чисел, які діляться на 3 або 5. Аналогічно .