3. Способи задання множин

Спосіб 1. Найбільш природним є спосіб задання множини переліком (або списком) елементів.

Наприклад: .

Порядок елементів у записі множини значення не має:

.

Вважається, що всі елементи множини різні. Цей спосіб завдання застосовується лише для скінчених множин з невеликим числом елементів. Іноді множини задають переліком частини множини, з якого можна зрозуміти, що являє собою вся множина.

Приклади стислого представлення множин:

• ;

• ;

• .

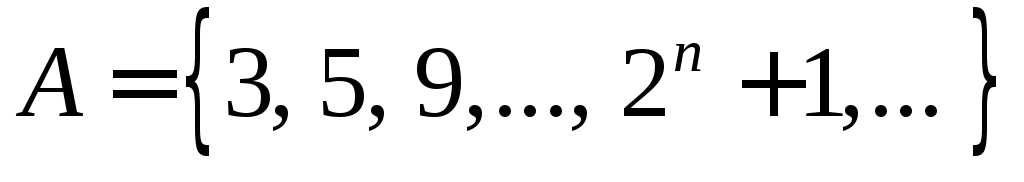Спосіб 2. Універсальним є задання множини за допомогою характерних властивостей її елементів (тобто властивостей, які мають всі елементи даної множини і лише вони). Наприклад:

• ;

• ;

• .

Спосіб 3. Аналітичний, за допомогою символів операцій над множинами та дужок.

Наприклад, (незнайомі символи будуть описані в наступному підрозділі).

Спосіб 4. Вербальний (мовний) за допомогою опису характерних властивостей, які повинні мати елементи множини.

Наприклад, множина А – це множина, елементами якої є всі назви днів тижня.

Спосіб 5. Множини зручно задавати графічно за допомогою діаграм Ейлера-Венна. Діаграми Ейлера-Венна (Джон Венн (1834-1923) англійський логік і математик, професор Кембриджського університету) є геометричним зображенням множин. Множина зображується замкненою кривою довільної форми (найчастіше – кругом). Точки, які лежать всередині замкненої кривої, можна розглядати як елементи відповідної множини.

Наприклад:

Універсум на діаграмах Ейлера-Венна зображується у вигляді прямокутника.

На наступній діаграмі Ейлера-Венна задані множини , в універсумі :

4. Операції над множинами

Вважаємо, що всі множини, що розглядаються, є підмножинами деякого універсуму U.

Означення 4.1. Об'єднанням двох множин та називається множина ,що складається з усіх елементів, що належать хоча б одній з множин , :

,

де– знак об’єднання.

На діаграмі Ейлера-Венна об’єднання показується сірим кольором:

Об’єднання складається з усіх елементів множини та усіх елементів множини і не містить ніяких інших елементів.

Операція об’єднання узагальнюється на довільну кількість множин. У такому випадку використовується позначення:

Приклад 4.1.

• _,

• _,

• _, ▲

Означення 4.2. Перерізом двох множин та називається множина, що складається з тих і лише тих елементів, що належать і _, і В:

,

де– знак перерізу.

На діаграмі Ейлера-Венна переріз показаний сірим кольором:

Операція перерізу узагальнюється на довільну кількість множин. У такому випадку використовується позначення:

Приклад 4.2.

• , ,;

• , ,;

• , ,

• {прямокутники},{ромби},{квадрати}.▲

Означення 4.3. Різницею множин і називається множина , що складається з усіх тих елементів множини ,які не належать :

,

де – знак різниці.

Приклад 4.3.

• , ,,;

• , ,;

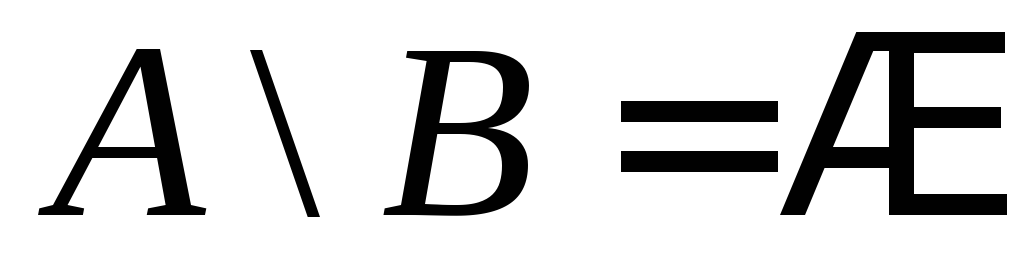• , {непарні числа},{парні числа}.▲

В означенні різниці, не розглядається випадок . Якщо, то різниця називається доповненням множини В до множини і позначається .

Зобразимо поняття різниці множин за допомогою діаграм Ейлера-Венна:

ТЕОРЕМА 4.1.

Доведення. , тоді

Означення 4.4. Різниця універсальної множини і будь-якої її підмножини А називається доповненням множини до універсальної .Позначається .

На діаграмі Ейлера-Венна доповнення показане сірим кольором:

Закони теорії множин

Для роботи із множинами часто використовують закони, наведені у таблиці 4.1.

Таблиця 4.1.

Назви законів	Формулювання законів
Закони комутативності
Закони асоціативності
Закони дистрибутивності
Закон подвійного доповнення
Закони ідемпотентності
Закони де Моргана
Закони поглинання
Закони тотожності
Закон домінування

Означення 4.5. Симетричною різницею двох множин та називається різниця об’єднання і перерізу даних множин та позначається

.

Геометрична ілюстрація:

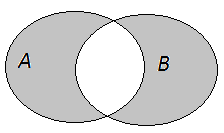
Приклад 4.4.

Розглянемо множини,

.▲

Використовуючи операції ¸¸ \¸можна виражати одні множини через інші. Існує наступний пріоритет операцій:. Для зміни цього порядку у виразі використовують дужки.

Таким чином, множину можна задати виразом, в який входять множини, операції і можуть бути дужки. Такий спосіб задання множини називається аналітичним.

Приклад 4.5. Нехай ;;;.

;

;

.▲

Означення 4.6. Кортеж – це впорядкований набір елементів.

Означення 4.7. Компоненти кортежу – елементи, що утворюють кортеж.

На відміну від множини, компоненти кортежу можуть повторюватись. Кортеж записують у круглих дужках, наприклад, (a, b, c, a, d, k) – кортеж довжиною 6. Кортежі довжини два часто називають парами, а довжини 3 – трійками.

Означення 4.8. Два кортежі називаються рівними, якщо вони мають однакову довжину та їхні відповідні компоненти рівні. Тобто, кортежі та рівні, якщо m=n, а також

Означення 4.9. Декартовим добутком двох множин таназивається множина всіх впорядкованих пар (a,b):

Якщо A=B, то такий добуток називають декартовим квадратом множини А:

Аналогічно можна ввести декартовий добуток трьох , чотирьох і т.д. множин. При скорочено пишуть і кажуть про n-й декартовий степінь множини A. Елементами є послідовності (набори, вектори, рядки) () довжиною n.

Приклад 4.6.

1. Нехай Тоді

2. Нехай – множини символів, які позначають горизонтальні і вертикальні поля шахівниці. Тоді – множина всіх кодів кліток шахівниці.▲

Для скінченних множин потужність (кількість елементів) декартового добутку дорівнює добутку потужностей цих множин: