Список літератури

1. Попович М.Г., Ковальчук О.В. Теорія автоматичного керування: Підручник. – Київ: Либідь, 1997. – 544 с.

2. Теорія автоматичного управління: Підручник/За ред. Г.Ф. Зайцева. – К.:Техніка, 2002. – 668 с.

3. Теорія автоматичного керування: Навчальний посібник./Л.М. Артюшин, Б.В. Дурняк,О.А. Машков, М.С. Сівов. – Львів:Вид-твоУАД, 2004. – 272 с.

4. В.А. Бесекерский, У.П. Попов Теория систем автоматического управления. - СПб:Изд-во "Профессия", 2004. – 752 с. – (Серия: Специалист)

5. Теория автоматического управления: Учебник /Под ред. А.В. Нетушила - М.:Высшая школа, 1983. - 432 с.

6. И.В. Мирошник Теория автоматического управления. Линейные системы. – СПБ:Питер, 2005. – 336 с.

7. Теория автоматического управления. Учебное пособие /Под ред. А.С. Шаталова - М.:Высшая школа, 1977. - 448 с.

8. Воронов А.А., Титов В.К., Новогренов Б.Н. Основы теории автоматического регулирования и управления: Учебное пособие. - М.:Высшая школа, 1977. – 519 с.

Навчальне видання

Дослідження стійкості лінійних систем автоматичного регулювання методичні вказівки

для самостійної підготовки та інструкція до лабораторної роботи № 6

з дисципліни «Теорія автоматичного керування» для студентів базового напрямку “Автоматизація і комп’ютерно-інтегровані технології”

Укладачі Крих Ганна Бориславівна,

Матіко Федір Дмитрович,

Дубіль Роман Ярославович

Редактор

Комп’ютерне верстання

Застосовуючи формулу Ейлера , а також формулу тригонометричних перетворень, одержимо

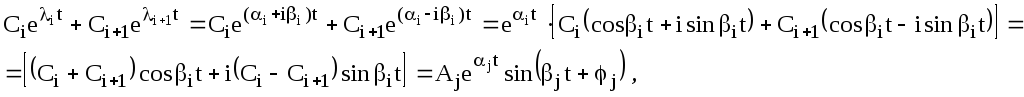де , а.

33