Приклад виконання завдання а) Дослідження стійкості сар за допомогою критерію Гурвіца

Завдання: Дослідити стійкість системи автоматичного регулювання з П-регулятором, структурна схема якої показана на рис.11. Функція передачі об’єкту регулювання

,

де - коефіцієнт передачі об’єкту регулювання;сталі часу аперіодичних ланок.

Функція передачі автоматичного П-регулятора

,

де - коефіцієнт передачі регулятора.

Для дослідження стійкості системи автоматичного регулювання за критерієм Гурвіца необхідно отримати характе-ристичне рівняння замкнутої САР. Функція передачі заданої САР має вигляд

.

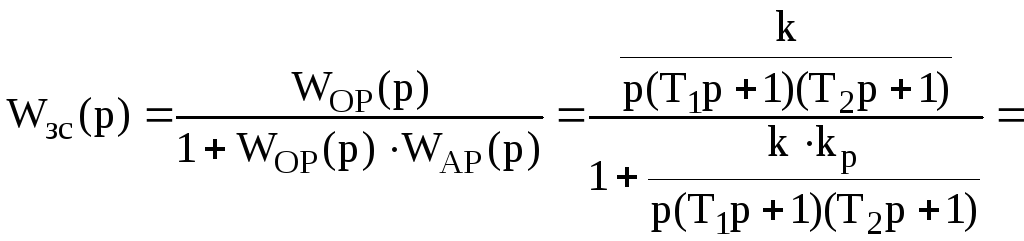
Характеристичне рівняння одержимо, прирівнявши знаменник отриманої функції передачі (характеристичний поліном системи) до нуля

.

Після розкриття дужок отримаємо

.

Загальний вигляд характеристичного рівняння третього порядку є таким

.

Тобто для досліджуваної системи ;;;. Як бачимо, всі коефіцієнти є одного знаку (додатними) при будь-яких значеннях коефіцієнта передачі П-регулятора, отже необхідна умова стійкості виконується.

Для визначення умов стійкості сформуємо головний визначник Гурвіца

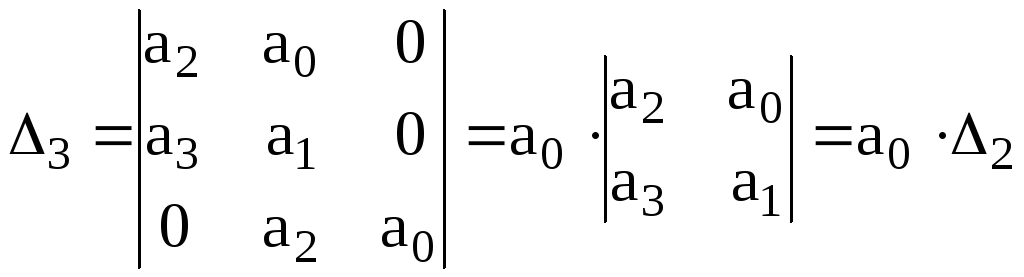
та визначники діагональних мінорів нижчих порядків

,

.

Досліджувана система буде стійкою, якщо >0 і>0 і>0. Визначникє додатний, знаквизначається тільки знаком, тому для того, щоб САР була стійкою достатньо щоб>0. Якщо, то САР буде на границі стійкості, при- нестійка.

Знайдемо критичне значення коефіцієнта передачі П-регулятора, при якому система буде знаходитися на границі стійкості з рівняння

.

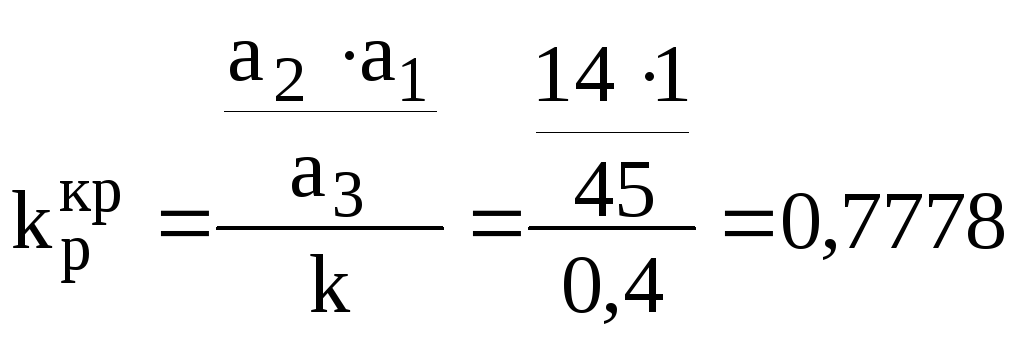Для забезпечення стійкості САР, значення коефіцієнта передачі П-регулятора повинно бути меншим від критичного . Якщо коефіцієнт передачі регуляторавиявиться більшим за критичне значення, то система буде нестійкою.

Змоделюємо досліджувану САР в середовищі Simulink:

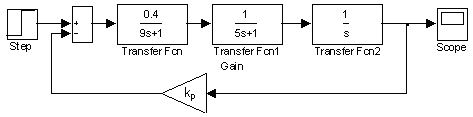
Рис 12. Структурна модель САР з П-регулятором.

Перехідна функція, отримана при критичному значенні =0,7778, показана на рис.13.

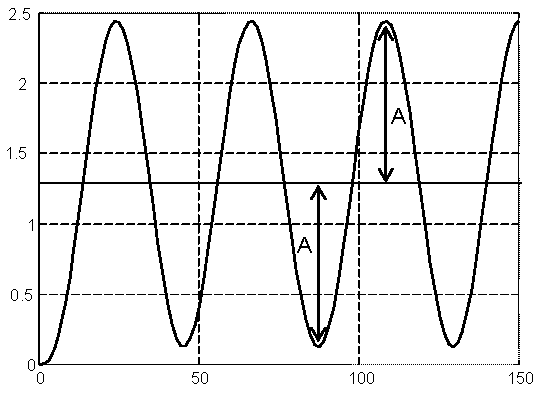
Рис. 13. Перехідна функція САР, отримана при =0,7778.

Перехідна функція є коливною із незаникаючими коливаннями. Усталені коливання здійснюються відносно значення вихідної величини 1,286. Амплітуда усталених коливань А=1,164, період коливань 42 с.

Змоделюємо перехідну функцію САР із значенням коефіцієнта передачі П-регулятора, меншим за критичне значення =0,7778, наприклад при=0,5 (рис. 14).

Усталене значення вихідної величини після завершення перехідного процесу (статична похибка регулювання) дорівнює 2. Період коливань становить 51 с, коефіцієнт заникання коливань 0,45.

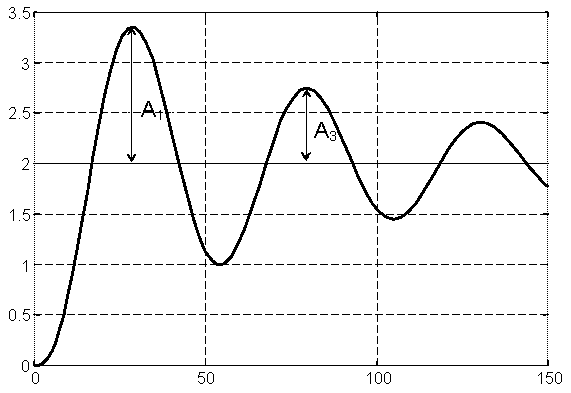
Рис. 14. Перехідна функція САР, отримана при =0,5.

Далі змоделюємо перехідну функцію САР із значенням коефіцієнта передачі П-регулятора, більшим за критичне значення, наприклад при =1 (рис. 15). Отриманий перехідний процес в САР є коливним, розбіжним. Коливання здійснюються відносно значення регульованої величини, що дорівнює 1. Період коливань 38 с.

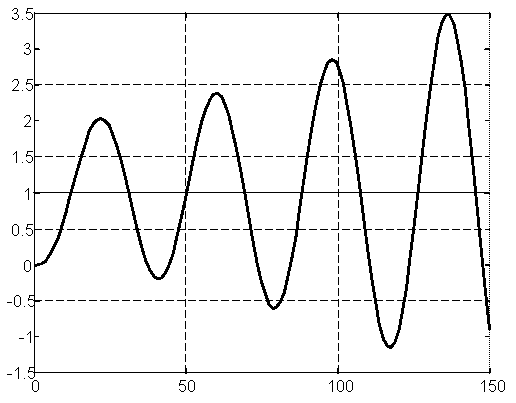
Рис. 15. Перехідна функція САР, отримана при =1.

Висновок: Таким чином, розраховане критичне значення параметра настроювання П-регулятора =0,7778 дійсно виводить систему на границю стійкості. Якщо=0,5, то САР є стійкою, при=1>0,7778 САР стає нестійкою. Отримані перехідні функції САР підтверджують правильність розрахунку критичного значення коефіцієнта передачі П-регулятора за критерієм Гурвіца. Перехідні процеси в САР є коливними, період коливань зменшується із збільшенням коефіцієнта передачі П-регулятора. Дослідження заданої САР показує, що із зменшенням коефіцієнта передачі П-регулятора статична похибка регулювання збільшується, що чітко обґрунтовується теоретично.

б) Дослідження стійкості САР за допомогою критерію Найквіста

Завдання: Об’єктом дослідження в другій частині лабораторної роботи є та сама САР, що і в першій частині.

Задане значення запасу стійкості САР: запас стійкості по фазі =35^о.

Задані зміни параметрів ОР: (збільшення коефіцієнта передачі ОР на 20%).

За допомогою критерію Найквіста розрахувати критичне значення параметра настроювання П-регулятора, а також таке його значення, що забезпечує заданий запас стійкості САР. Дослідити перехідну функцію САР із заданим запасом стійкості, а також дослідити вплив збільшення коефіцієнта передачі ОР.

Для того щоб спростити знаходження виразів частотних характеристик, функцію передачі об’єкта регулювання доцільно представити як добуток функцій передачі інтегруючої і двох аперіодичних ланок, тобто представити послідовним з’єднанням цих ланок, як показано на рис.16.

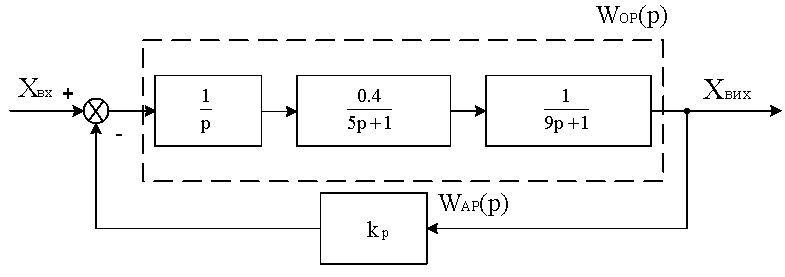
Рис. 16. Структурна схема досліджуваної САР.

Згідно з критерієм Найквіста амплітудно-фазова-характеристика (АФХ) САР, що знаходиться на границі стійкості проходить через точку (-1,і0), тобто виконується умова (25)

або

,

де - амплітудно-фазова характеристика розімкнутої системи;амплітудно-частотні характеристики об’єкта регулювання і автоматичного регулятора відповідно;фазочастотні характеристики відповідно об’єкта регулювання і автоматичного регулятора.

Визначимо необхідні амплітудно- і фазочастотні характеристики. Відомо, що АЧХ послідовного з’єднання елементів дорівнює добутку амплітудно-частотних характеристик елементів, що складають з’єднання, а ФЧХ – сумі їх фазочастотних характеристик. Відповідно АЧХ і ФЧХ об’єкту регулювання матимуть вигляд

,

АЧХ і ФЧХ П-регулятора -

.

Знайдені вирази характеристик підставимо в систему (25)

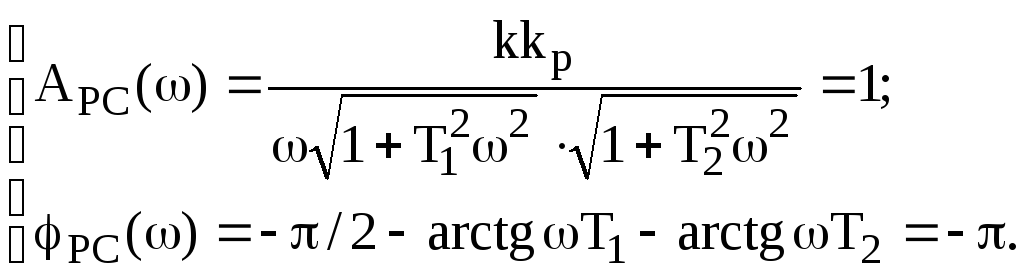
З врахуванням заданих значень параметрів моделей запишемо

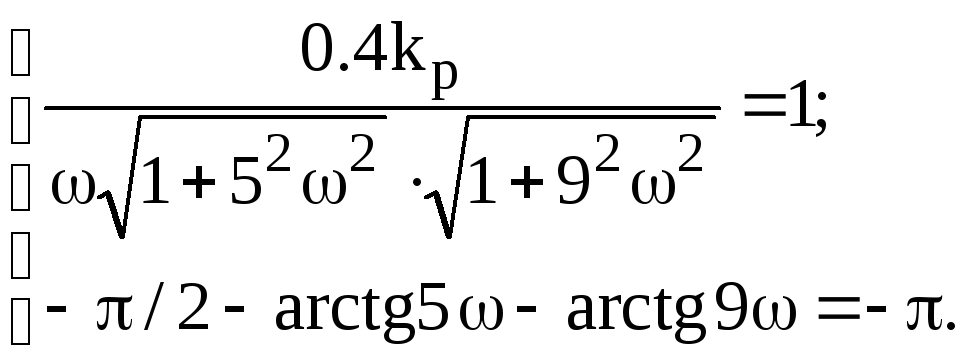
З другого рівняння системи визначимо частоту а з першого - критичне значення коефіцієнта передачі П-регулятора

.

Друге рівняння системи, як бачимо, аналітично не розв’язується, тому значення знайдемо числовим методом із застосуванням функції fzero в Matlab.

Для розрахунку параметрів, при яких САР буде на границі стійкості, та побудови АФХ виконаємо наступну програму в Matlab:

%знаходження

wp0=1;

wpi=fzero('fff',wp0),

%розрахунок критичного значення к_р

A1=0.4/sqrt(1+wpi^2*25);

A2=1/sqrt(1+wpi^2*81);

A3=1/wpi;

kr=1/A1/A2/A3,

%побудова АФХ розімкнутої САР на границі стійкості

w=[0:0.01:5];

A1=0.4./sqrt(1+w.^2*25);

A2=1./sqrt(1+w.^2*81);

A3=1./w;

A4=kr;

fi1=-atan(w*5);

fi2=-atan(w*9);

fi3=-pi/2;

fi4=0;

A=A1.*A2.*A3.*A4;

fi=fi1+fi2+fi3+fi4;

polar(fi,A), grid;

де

function y=fff(w);

y=-atan(w*5)-atan(w*9)-pi/2+pi;

В результаті виконання програми отримаємо розв’язок системи: ,На рис. 17 показана амплітудно-фазова характеристики розімкнутої системи, яка підтверджує, що розрахунок критичного значення П-регулятора виконаний правильно, оскільки АФХ проходить через точку з радіусом 1 і кутом 180⁰, що відповідає точці (-1, і0) в декартових координатах.

Для розрахунку значення коефіцієнта , при якому забезпечується заданий запас стійкості системи по фазі, частоту зрізурозраховують з другого рівняння системи

,

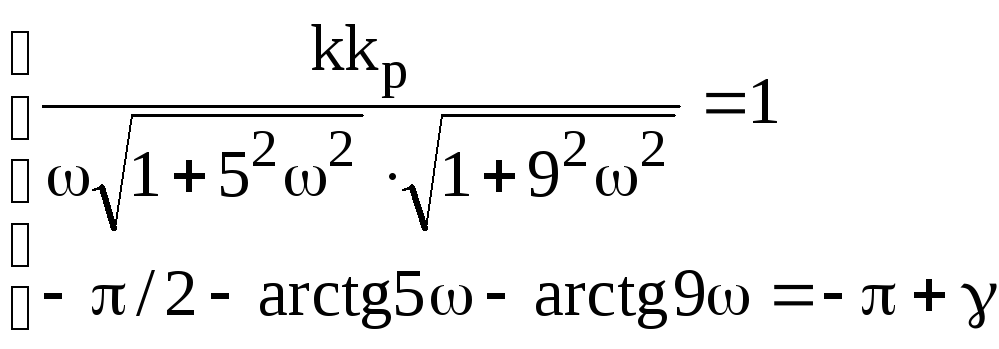а з першого визначають значення .

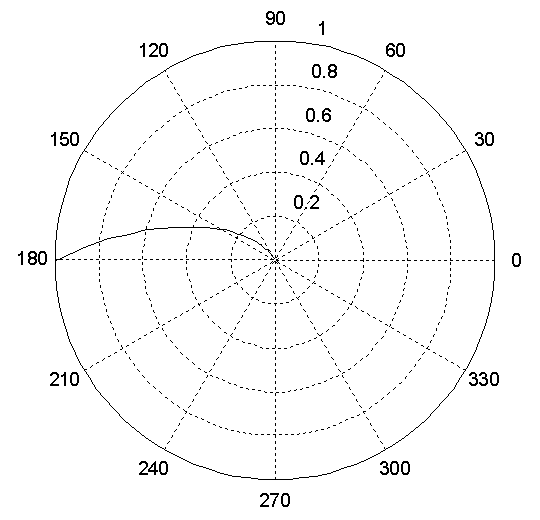
Рис. 17. АФХ розімкнутої САР (замкнута САР на границі стійкості).

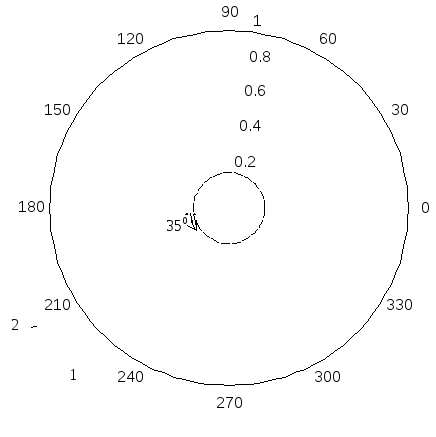
Рис. 18. АФХ розімкнутої САР із заданим запасом стійкості по фазі (крива 1) та АФХ системи із коефіцієнтом передачі об’єкта регулювання (крива 2).

Для розрахунків скористаємося наведеною вище програмою, яка відрізнятиметься від неї лише виглядом допоміжної функції y, а саме

function y=fff(w);

ga=35*pi/180;

y=-atan(w*5)-atan(w*9)-pi/2+pi-ga;

В результаті виконання програми отримуємо значення частоти зрізу і коефіцієнта передачі П-регулятора k = 0,2449. На рис. 18 (крива 1) показана АФХ розімкнутої САР при розрахованому значенні параметра регулятора, з якої видно, що запас стійкості САР становить 35⁰.

Побудуємо також перехідну функцію розрахованої САР.

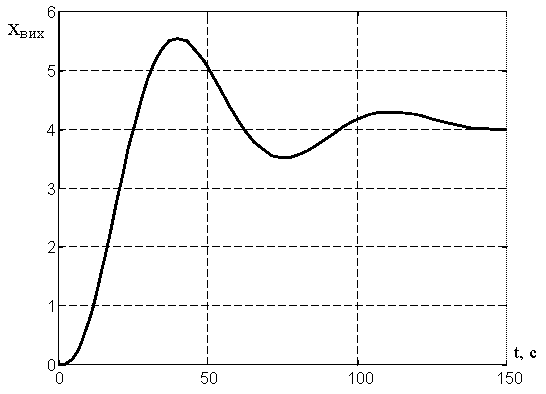
Рис. 19. Перехідна функція САР із заданим запасом стійкості по фазі.

Статична похибка регулювання дорівнює 4,08, А₁ = 5,55-4,08=1,47, А₃ = 4,3-4,08=0,22 і коефіцієнт заникання коливань .

Далі оцінимо вплив збільшення коефіцієнта передачі ОР (=0,48) на перехідну функцію. Як видно із рис. 20, для перехідної функції системи регулювання із статична похибка регулювання дорівнює 4,08, перша амплітуда , третя амплітуда, коефіцієнт заникання коливань . Для порівняння на рис. 20 пунктирною лінією показана також перехідна функція з рис. 19.

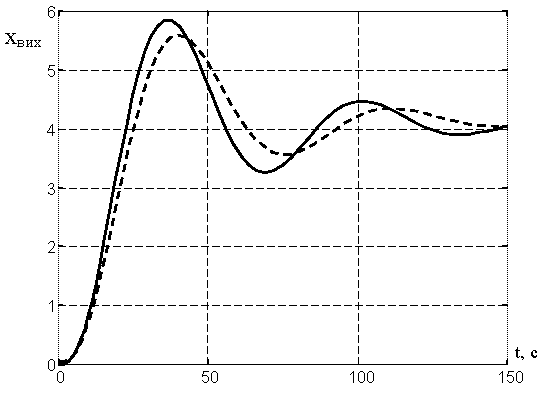
Рис. 20. Перехідні функції САР з коефіцієнтом передачі ОР k=0,4 (штрихова лінія) та коефіцієнтом передачі k=0,48 (суцільна лінія).

Порівнюючи ці два графіка, бачимо, що при збільшенні коефіцієнта передачі ОР статична похибка регулювання не змінилася, а запас стійкості САР зменшився, оскільки коефіцієнт заникання зменшився з 0,85 до 0,79. Зменшення запасу стійкості САР із збільшеним коефіцієнтом передачі ОР на 20% проілюстровано також за допомогою АФХ розімкнутої системи на рис.18 (крива 2), з якої видно, що запас стійкості по фазі зменшився до 30⁰, а запас стійкості по амплітуді з 0,67 до 0,6.

Висновок: Знайдене критичне значення параметру П-регулятора за допомогою критерію Найквіста збігається з розрахованим за критерієм Гурвіца, що підтверджує правильність розрахунків. Застосування критерію Найквіста дозволяє розраховувати САР на заданий запас стійкості. Дослідження заданої САР показують, що із збільшенням коефіцієнта передачі ОР запас стійкості САР зменшується і по фазі, і по амплітуді.