3. Запас стійкості систем автоматичного регулювання

Реальні системи повинні бути не тільки стійкими, але й мати певний запас стійкості, тобто повинні знаходитися на деякій відстані від границі стійкості. В протилежному випадку незначні зміни параметрів системи можуть призвести до її нестійкості і непридатності для роботи. На практиці проектування САР здійснюють переважно, виходячи не тільки з умов стійкості, але й з умов забезпечення потрібної якості перехідного процесу. З цією метою розрахунок САР проводять з умови забезпечення запасу стійкості.

Запас стійкості – це кількісна оцінка відстані значень параметрів системи або її характеристик від зони, небезпечної з точки зору стійкості

Запас стійкості САР можна оцінити за критерієм Найквіста. Чим ближче наближається АФХ розімкнутої системи до точки (-1, і0), тим менше її запас стійкості в замкнутому стані. Кількісно запас стійкості оцінюють за амплітудою і фазою (див. рис. 10 ).

Запас стійкості по амплітуді дорівнює відстані від точки перетину дійсної осі амплітудно-фазовою характеристикою розімкнутої системи до точки

, (26)

де - частота, при якій зсув фаз розімкнутої системи досягає –π, і відповідно- це є значення амплітудно-частотної характеристики розімкнутої системи при.

Запас стійкості за фазою оцінюється за кутом між від’ємною частиною дійсної осі і лінією, проведеною через початок координат і точку перетину АФХ з колом одиничного радіуса

, (27)

де - частота зрізу, тобто частота, при якій амплітудно-частотна характеристика розімкнутої системи досягає одиниці;- значення зсуву фаз між вихідним та вхідним сигналом розімкнутої системи при частоті зрізу.

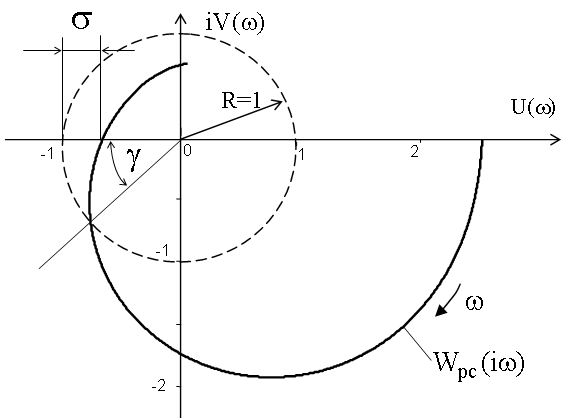
Рис. 10. Визначення запасу стійкості системи за фазою і амплітудою.

Незалежно від прийнятої форми, запас стійкості є кількісною характеристикою і використання його при розрахунках САР є гарантією стійкості системи в реальних умовах.

Висновки. Стійкість є основною вимогою до роботи САР, і відповідно дослідження стійкості є одним з основних етапів синтезу системи автоматичного регулювання. За наявності математичної моделі САР оцінка стійкості САР, а також аналіз впливу параметрів системи на стійкість може успішно здійснюватись за допомогою одного з розглянутих критеріїв.

Послідовність виконання роботи

Змістом виконання роботи є дослідження стійкості заданої системи автоматичного регулювання. За допомогою критеріїв Гурвіца (частина 1) і Найквіста (частина 2) необхідно визначити критичні значення коефіцієнтів настроювання автоматичного регулятора, а також значення параметрів настроювання, що забезпечують заданий запас стійкості за амплітудою або за фазою. Далі в середовищі Matlab-Simulink складають структурну схему системи і в результаті моделювання отримують перехідні функції замкнутої системи. Вихідними даними для виконання лабораторної роботи є функція передачі об’єкту регулювання з конкретними числовими значеннями параметрів, та функція передачі автоматичного регулятора з невідомими параметрами настроювання.

В частині 1 лабораторної роботи студентові необхідно:

1. Скласти характеристичне рівняння заданої САР, розрахувати числові значення його коефіцієнтів.

2. Скласти визначник Гурвіца та розрахувати критичні значення параметрів настроювання регулятор.

3. Скласти структурну схему замкнутої системи в Simulink, встановити задані та розраховані значення коефіцієнтів моделей.

4. Здійснити моделювання САР при одиничній стрибкоподібній зміні вхідної величини та отримати перехідну функцію САР.

5.Дослідити вплив зміни параметрів настроювання регулятора на перехідний процес в замкнутій системі. Порівняти перехідні функції, отримані принаймні при трьох значеннях параметрів настроювання регулятора (рівних, менших та більших за критичне значення), визначаючи кожний раз характер та вигляд перехідної функції, а також коефіцієнт заникання перехідного процесу, де А₁, А₃ – відповідно перша та третя амплітуди коливного процесу.

В частині 2 лабораторної роботи студентові необхідно:

1. На основі критерію Найквіста, розрахувати критичні значення параметрів настроювання заданого регулятора.

2. Розрахувати значення параметрів настроювання регулятора на заданий викладачем запас стійкості по фазі або по амплітуді.

3. Побудувати в середовищі Matlab амплітудно-фазові характеристики розімкнутої САР при розрахованих значеннях параметрів настроювання регулятора та оцінити графічно запас стійкості системи за фазою та амплітудою.

4. Скласти структурну схему замкнутої САР в Simulink, встановити задані значення параметрів об’єкта регулювання та розраховані значення параметрів регулятора.

5. Здійснити моделювання САР при одиничній стрибкоподібній зміні вхідної величини та отримати перехідні функції САР для критичного значення параметру регулятора та для параметра регулятора, що забезпечує заданий запас стійкості.

6. Дослідити вплив зміни параметрів об’єкта регулювання (наприклад, збільшення запізнення, збільшення-зменшення сталих часу, збільшення-зменшення коефіцієнта передачі) на перехідний процес в САР. Для цього порівняти перехідні функції при різних значеннях параметрів системи, кожний раз визначаючи коефіцієнт заникання та запас стійкості САР за амплітудою і фазою.