2.2. Дослідження стійкості сар за допомогою критерію Найквіста

На відміну від критерію Гурвіца, що встановлює приналежність коренів до лівої півплощини для будь-якої системи з відомим характеристичним рівнянням, критерій Найквіста призначений для дослідження тільки замкнутих систем. Критерій Найквіста – це графоаналітичний критерій. Характерною особливістю його застосування є те, що висновок про стійкість замкнутої САР роблять на основі вигляду амплітудно-фазової характеристики (АФХ) або логарифмічних частотних характеристик розімкнутої САР. Крім дослідження стійкості за виглядом вказаних частотних характеристик можна оцінити якісні показники замкнутої САР, наприклад запас стійкості. Більш того, можна легко зорієнтуватись за рахунок чого нестійку замкнуту систему перетворити на стійку.

Функцію передачі замкнутої САР (рис. 5), що є зустрічно паралельним з’єднанням, елементів можна представити у вигляді

. (13)

Функцію передачі розімкнутої САР (відсутній зворотний зв’язок), що є послідовним з’єднанням об’єкта регулювання і автоматичного регулятора, запишемо у вигляді добутку відповідних їм функцій передачі

. (14)

З врахуванням рівняння (13) функцію передачі замкнутої САР запишемо у вигляді

. (15)

Функцію передачі розімкнутої системи також представимо у вигляді відношення поліномів

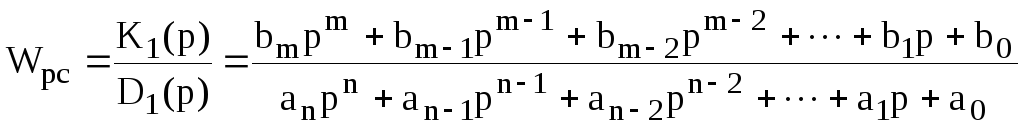, (16)

де - характеристичний поліном розімкнутої системи. Степінь полінома чисельника не може бути більше степені полінома знаменника. Підставляючи (16) в (15), одержимо

,

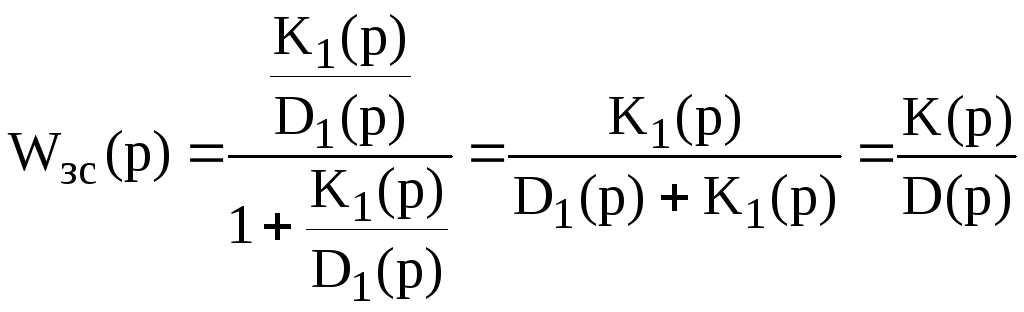де - характеристичний поліном замкнутої системи. Сформуємо нову функцію, як відношення характеристичних поліномів замкнутої та розімкнутої системи

. (17)

В загальному випадку імають однакову степінь. У виразіполіноми чисельника і знаменника також мають однакову степінь, це означає, що чисельник і знаменник мають однакову кількість коренів. Корені полінома чисельника будь-якої функції передачі називаютьсянулями, а корені полінома знаменника - полюсами.

Запишемо в полюсно-нульовому представленні

(18)

де - нулі,- полюси;- коефіцієнт передачі розімкнутої системи (в полюсно-нульовому сенсі). В загальному випадку коренііможуть бути як дійсними так і комплексними.

При підстановці у вираз (18) одержимо частотну характеристику

. (19)

Кожний множник або у виразі (19) в комплексній площині можна розглядати як різницю векторів таабота(рис. 6). Початок векторабуде знаходитись в точці, а кінець на уявній осі. Якщо змінювати частоту віддо, то кінець векторабуде ковзати вздовж уявної осі і повертатися на кут. Якщо корінь (дійсний або комплексний) розміщений зліва від уявної осі, то обертання здійснюється проти годинникової стрілки і кутвважається додатним. Якщо корінь розміщений справа, то обертання, наприклад, вектораздійснюється за годинниковою стрілкою, кут обертанняє від’ємним і при зміні частоти віддодорівнює.

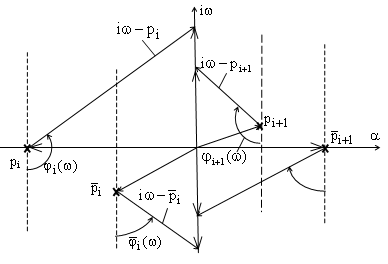
Рис. 6. Ілюстрація обертання векторів тав комплексній площині

при розміщенні нулів та полюсів зліва та справа від уявної осі.

Якщо кожне комплексне число чисельника і знаменникавиразу (19) записати в показниковій формі, то одержимо

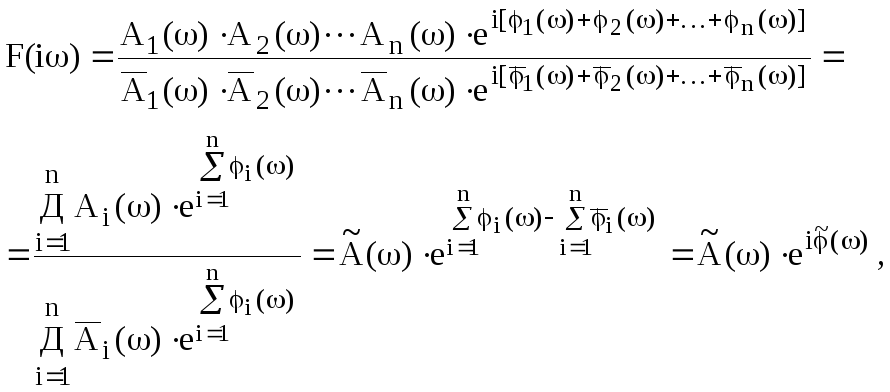(20)

де модуль і-ого комплексного числа відповідно чисельника і знаменника;,- аргумент і-ого комплексного числа відповідно чисельника і знаменника;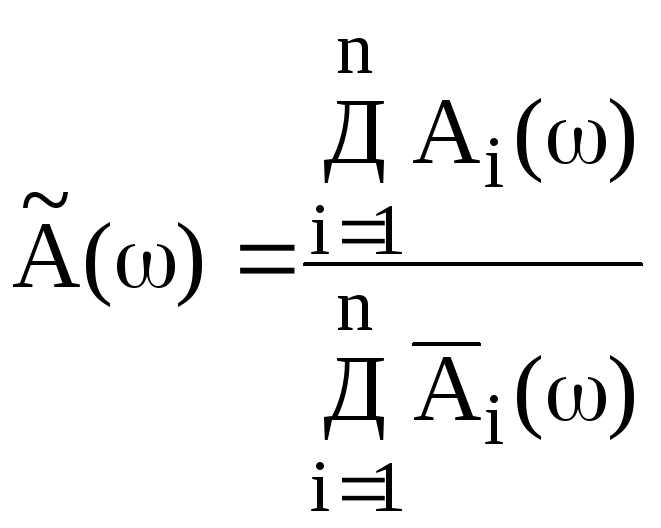- модуль. Аргументзгідно (20) визначається як різниця між сумою кутів повороту всіх векторів чисельника і сумою кутів повороту всіх векторів знаменника, тобто

. (21)

Припустимо, що характеристичне рівняння замкнутої САР має l правих коренів, тоді лівих коренів є n-l, а характеристичне рівняння розімкнутої системи має k правих коренів і лівих коренів. Тоді згідно рівнянь (19) і (21) зміна аргументупри зміні частоти віддодорівнюватиме

. (22)

В стійкій замкнутій системі всі дійсні корені мають бути від’ємними, а комплексні мати від’ємну дійсну частину, тобто бути лівими, тоді і зміна аргументу, як видно з рівняння (22) буде такою

.

При зміні частоти від 0 до зміна аргументубуде вдвічі меншою

. (23)

Як видно з рівняння (19) є по суті амплітудно-фазовою характеристикою САР в розімкнутому стані, зміщеною на 1.Згідно з критерієм Найквіста для стійкості замкнутої системи автоматичного регулювання необхідно і достатньо, щоб при зміні частоти від нуля до нескінченості, вектор , початок якого знаходиться в точці (-1, і0) комплексної площини, а кінець на амплітудно-фазовій характеристиці розімкнутої системи, повернувся в додатному напрямі (проти годинникової стрілки) на кут, деk – кількість додатних (правих) коренів характеристичного рівняння розімкнутої системи.

Інакше кажучи, зміна аргументу при зміні частоти від нуля до нескінченості в стійкій замкнутій системі дорівнюватиме.

Таким чином, якщо розімкнута система автоматичного регулювання є нестійкою, то це не означає що вона буде нестійкою в замкнутому стані. Вона може бути і стійкою, і нестійкою.

Розглянемо застосування критерію Найквіста для випадку, коли розімкнута система є стійкою. Якщо розімкнута система стійка (тобто додатні корені характеристичного рівняння відсутні і k=0), то для того, щоб система була стійкою в замкнутому стані, зміна аргументу при зміні частоти від 0 до +згідно (23) має дорівнювати нулю

. (24)

Для прикладу на рис. 7 показано напрям руху вектора для розімкнутої системи другого порядку з характеристичним рівнянням, дійсні корені якого є від’ємними. До точки В векторпри збільшенні частоти повертається за годинниковою стрілкою на куті далі при зростанні частоти до нескінченності повертається проти годинникової стрілки на такий самий кут. Таким чином сумарний кут повороту цього вектора дорівнює нулю. Це означає, що в замкнутому стані система буде також стійкою.

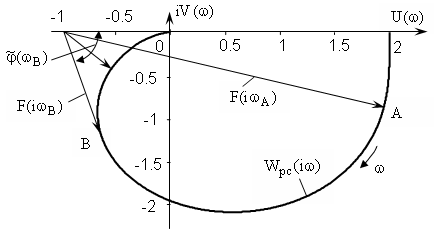
Рис. 7. Пояснення руху вектора вздовж АФХ розімкнутої системи.

На практиці для складних АФХ розімкнутих систем кути повороту вектора , визначити важко, тому користуються іншим, більш простішим правилом. Виявляється, що якщо точка (-1,і0) знаходиться поза АФХ стійкої розімкнутої системи, то кут повороту векторабуде завжди дорівнювати нулю. Тому критерій Найквіста для цього випадку можна сформулювати так:якщо амплітудно-фазова характеристика стійкої розімкнутої системи не охоплює точку (-1,і0), то замкнута система буде стійкою. Користуючись цим формулюванням легко бачити, що стійка розімкнута система з АФХ, показаною на рис. 8,а) буде нестійкою в замкнутому стані, а система на рис.8,б) - стійкою.

Якщо АФХ розімкнутої системи в комплексній площині проходить через точку (-1,і0), то замкнута система буде знаходитися на границі стійкості. Аналітично ця умова записується у вигляді

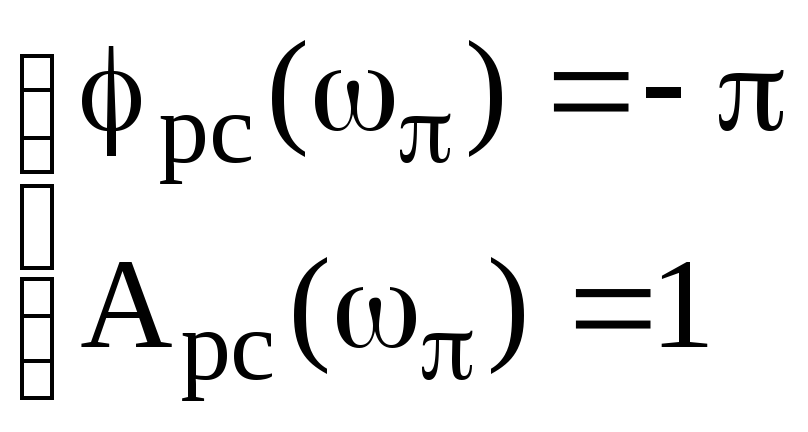, (25)

де - відповідно амплітудно-фазова, амплітудно-частотна та фазочастотна характеристики розімкнутої системи;- частота, при якій ФЧХ розімкнутої системи досягає значення.

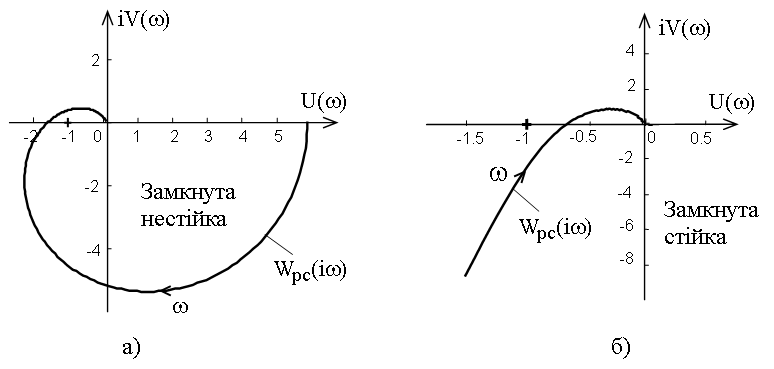
Рис. 8. Амплітудно-фазові характеристики розімкнутих стійких систем (k=0).

Розглянемо застосування критерію Найквіста для випадку, коли розімкнута система є нестійкою, і її характеристичне рівняння містить k правих коренів. Для встановлення стійкості таких систем в замкнутому стані визначають кут повороту вектора, який згідно критерію Найквіста має дорівнювати, де k – кількість правих коренів характеристичного рівняння розімкнутої системи

Однак на практиці зручніше користуватись іншим формулюванням критерію Найквіста. САР, нестійка в розімкнутому стані, буде стійкою в замкнутому, якщо при зміні частоти від 0 до +різниця між кількістю додатних і від’ємних переходів АФХ розімкнутої системи через відрізок дійсної осірівна.Від’ємним (-1) вважається перехід, при якому АФХ перетинає вісь знизу вверх, і навпаки – додатним (+1), якщо АФХ перетинає вісь зверху вниз. Якщо при АФХ розімкнутої системи бере початок з відрізкуто це відповідає 1/2 переходу з відповідним знаком. На рис. 9 показані АФХ нестійких розімкнутих систем, які при замиканні стають стійкими. На рис. 9, а АФХ розімкнутої нестійкої системи з одним правим коренем k=1 починається на відрізку дійсної осі та із зростанням частоти рухається зверху вниз і далі не перетинає вказаний відрізок, тобто кількість додатних переходів дорівнює1/2, тому в замкнутому стані система буде стійкою. На рис. 9, б АФХ розімкнутої нестійкої системи з двома правими коренями (k=2) перетинає відрізок дійсної осі один раз: зверху вниз (+1), від’ємних переходів немає, і це означає, що в замкнутому стані система буде стійкою, оскільки за критерієм Найквіста різниця між додатними і від’ємними переходами в стійкій системі має дорівнювати одиниці (k/2=2/2=1).

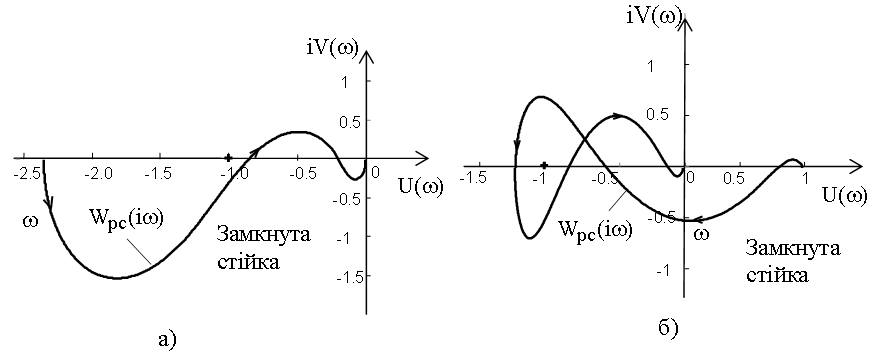
Рис. 9. Амплітудно-фазові характеристики розімкнутих нестійких систем:

а) k=1; б) k=2.