2. Встановлення стійкості сар за допомогою критеріїв стійкості

Якщо відомі параметри математичних моделей елементів САР (коефіцієнти передачі, сталі часу), то задачі встановлення коефіцієнтів характеристичного рівняння системи і визначення його коренів вирішуються відносно легко за допомогою засобів обчислювальної техніки. Але в теорії автоматичного керування обґрунтовані методи аналізу стійкості систем за допомогою критеріїв стійкості. Критерій стійкості – це математичне формулювання умов, яким повинні задовольняти коефіцієнти характеристичного рівняння або деякі функції цих коефіцієнтів, щоб система була стійкою. Критерії стійкості дозволяють не визначаючи коренів характеристичного рівняння, сформулювати умову стійкості за коефіцієнтами характеристичного рівняння. Цінність застосування критеріїв стійкості полягає не стільки в тому, що усувається необхідність визначати корені характеристичного рівняння, а в тому, що вони дають можливість встановити, як той чи інший параметр системи, її структура впливає на стійкість, і як їх необхідно змінити, щоб система стала стійкою.

Розроблені критерії стійкості поділяють на дві групи – алгебраїчні та частотні. До алгебраїчних критеріїв стійкості належать критерії Гурвіца, Рауса, до частотних – критерії Найквіста, Михайлова.

2.1. Дослідження стійкості сар за допомогою критерію Гурвіца

Необхідною (але недостатньою) умовою стійкості САР є те, що всі коефіцієнти характеристичного рівняння замкнутої системи повинні мати однаковий знак. В цьому випадку система може бути стійкою, але не виключена можливість її нестійкості. Тільки для систем першого і другого порядків необхідна умова стійкості є і достатньою. Якщо хоча б один коефіцієнт характеристичного рівняння відрізняється знаком від інших, то без жодних додаткових досліджень можна зробити висновок, що система є нестійкою.

Для систем порядку вищого за другий остаточний висновок про стійкість можна зробити, застосовуючи, наприклад, критерій Гурвіца.

Нехай досліджується система, модель якої задана у вигляді функції передачі

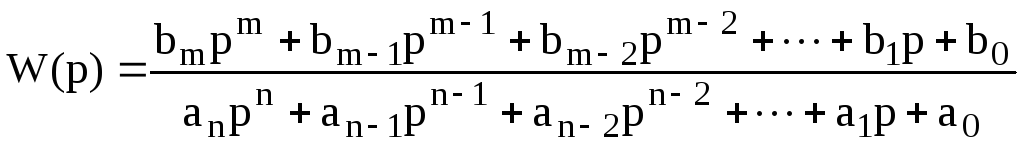. (10)

Характеристичне рівняння може бути отримане із знаменника функції передачі заміною оператора Лапласа р на змінну .

Критерій Гурвіца формулює умови стійкості у вигляді визначників, складених з коефіцієнтів характеристичного рівняння (5) системи. Достатню умову формулюють за допомогою визначника, складеного з коефіцієнтів характеристичного рівняння . Гурвіц запропонував складати цей визначник у вигляді квадратної матриці розміром

. (11)

В головній діагоналі виписують коефіцієнти характеристичного рівняння, починаючи з до. Стовпчики визначника вверх від головної діагоналі заповнюють коефіцієнтами із спадаючими індексами, а вниз від діагоналі – коефіцієнтами із наростаючими індексами. Всі місця коефіцієнтів з індексами меншими від 0 та з індексами більшими від n, а також відсутні коефіцієнти заповнюють нулями. Цей визначникназивається головним, і з нього складають мінори

, ,,…,. (12)

Для стійкості системи достатньо, щоб головний визначник Гурвіца, а також всі його діагональні мінори були одного знаку з коефіцієнтом (якщото і всі мінори мають бути додатними).

Умову перебування системи на границі стійкості отримують при нульовому значенні визначника Гурвіца, тобто . Це можливо приі при. Перша умова відповідає границі стійкості першого роду (аперіодична границя стійкості), а друга - границі стійкості другого роду (коливна границя стійкості).

Суттєвим недоліком критерію Гурвіца є те, що для рівнянь високих порядків (вище 4-ого) умови стійкості є достатньо громіздкими і тоді в кращому випадку можна сказати стійка система автоматичного регулювання чи нестійка. У випадку ж нестійкості системи критерій не дає відповіді на питання, як треба змінити параметри системи, щоб зробити її стійкою. Власне тому в інженерній практиці застосовують більш зручні критерії стійкості, зокрема частотний критерій Найквіста.