
- •Розв’язати рівняння з параметрами — означає знайти всі розв’язки цього рівняння для кожної допустимої системи значень параметрів.
- •12.1. Лінійні рівняння з параметром
- •12.2. Квадратні рівняння з параметром
- •Похідні обернених тригонометричних функцій:
- •Значення похідної в деякій точці дорівнює тангенсу кута, утвореного дотичною до кривої в цій точці з додатним напрямом осі Ох.
Значення похідної в деякій точці дорівнює тангенсу кута, утвореного дотичною до кривої в цій точці з додатним напрямом осі Ох.
Приклад. Знайти тангенси кутів нахилу дотичної до кривої у = х2 у точках М1(½; ¼), М2(–1; 1) (рис. 3).
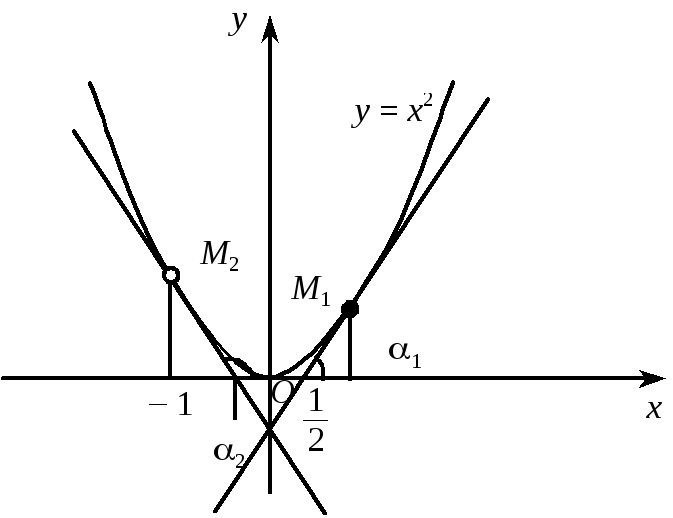
Рис. 3
-
Згідно з (6) дістаємо:

За
формулою похідної степеневої функції
маємо:
![]()
Отже,
![]()
![]()
Рівняння дотичної та нормалі до кривої
Розглянемо рівняння кривої у = f(x) (рис. 4). Візьмемо на кривій точку М(х1, у1) і запишемо рівняння дотичної до цієї кривої в точці М, припускаючи, що дотична не паралельна жодній координатній осі.
Рівняння кривої, що має кутовий коефіцієнт k і проходить через точку М, набирає вигляду
![]() .
.
Для
дотичної
![]() ,
тому рівняння дотичної буде таке:
,
тому рівняння дотичної буде таке:
![]()
Поряд із дотичною до кривої розглядають і її нормаль.
Нормаллю до кривої в даній точці називається пряма, яка проходить через цю точку і перпендикулярна до дотичної в ній.
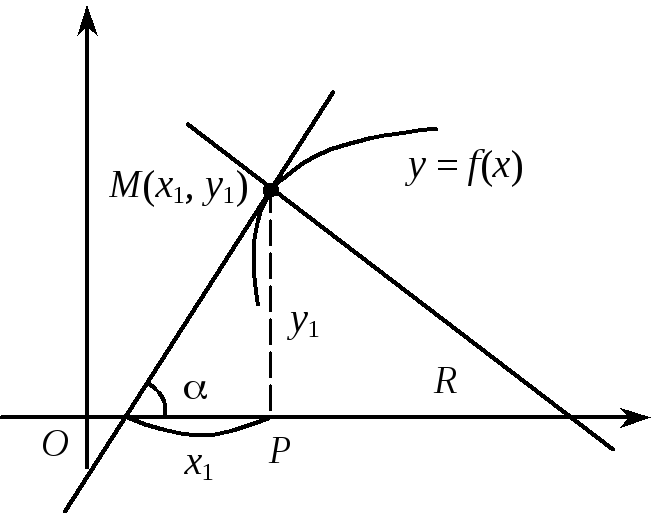
Рис. 4
Із означення нормалі випливає, що її кутовий коефіцієнт kнорм пов’язаний із кутовим коефіцієнтом k дотичної рівністю
![]() ,
тобто
,
тобто
![]()
Отже, дістаємо рівняння нормалі до кривої у = f(x) у точці М (х1, у1):
![]()
Приклад. Записати рівняння дотичної та нормалі до кривої у = х3 у точці М(1; 1).
Оскільки у = 3х2, то кутовий коефіцієнт дотичної
![]() .
.
Отже, згідно з (1) рівняння дотичної буде таке:
![]() ,
або
,
або
![]() .
.
Рівняння нормалі:
![]() ,
або
,
або
![]() (рис. 5).
(рис. 5).

Рис. 5
![]()
1. Знайти похідну функції.
1)
![]() ; 2)
; 2)
![]() ;
;
3)
![]() ; 4)
; 4)
![]() ;
;
5)
![]() ; 6)
; 6)
![]() ;
;
7)
![]() ; 8)
; 8)
![]() ;
;
9)
![]() ; 10)
; 10)
![]() .
.
2. В
якій точці похідна функції
![]() дорівнює 7?
дорівнює 7?
3. Скласти
рівняння дотичної до графіка функції
![]() в точці
в точці
![]() :
:
4. Знайти
![]() кута похилу графіка функції
кута похилу графіка функції
![]() в точці
в точці
![]()
5. В
яких точках графіка функції
![]() дотична до нього утворює тупий кут з
віссю абсцис?
дотична до нього утворює тупий кут з
віссю абсцис?
6. Знайти
![]() ,
якщо
,
якщо
![]() .
.
7. Знайти похідну функції.
1)
![]() ; 2)
; 2)
![]() ;
;
3)
![]() ; 4)
; 4)
![]() ;
;
5)
![]() ; 6)
; 6)
![]() ;
;
7)
![]() ; 8)
; 8)
![]() ;
;
9)
![]() ; 10)
; 10)
![]() .
.
8. Знайти
приріст функції
![]() в точці
в точці
![]() ,
якщо
,
якщо
![]() .
.
9. Вибрати
функцію, для якої не існує похідної в
точці
![]() .
.
1)
![]() ; 2)
; 2)
![]() ;
;
3)
![]() ;
4)
;
4) ![]() .
.
10. Розв’язати
рівняння
![]() ,
якщо:
,
якщо:
1)
![]() ; 2)
; 2)
![]() ;
;
3)
![]() ; 4)
; 4)
![]() .
.
