§.4. Социально-экономическая структура общества

4.1. Модель распределение богатства в обществе

Функция распределения богатства в обществе L(z), называемая также функцией Лоренца сообщает, что z-я часть самых бедных людей общества владеет L(z)-й частью всего общественного богатства. Далее приведен график функции L(z) , самая нижняя кривая. Площадь заштрихованной линзы называется коэффициентом Джинни J. Эта величина не более 1/2. Чем она меньше, тем равномернее распределено богатство в обществе. При J >0,2 распределение богатства называется опасно несправедливым — это преддверие социальных волнений. Из функции L(z) можно получить другую функцию w(z) , она сообщает долю общественного богатства, которой владеет z-я часть самых богатых людей.

w(z)=1— L(1 — z)

График функции w самая верхняя кривая. Еще одну функцию можно получить из L(z): пусть S(x)=L(1/2 + x) — L(1/2 — x).

Она показывает долю общественного богатства, которой владеет средний класс. График функции S, кривая расположена только над отрезком [0, 1/2]. Говорят, что в обществе есть средний класс, если L(3/4) — L(1/4)  1/2 или, что то же самое S(1/4)  1/2 .

Например, это значит, что , т. е. половина самых бедных владеет 41% всего богатства и т. д.

Дано: L(z) = 2^z— 1, для 0z1/2, а на отрезке [1/2,1] функциюL(z) непрерывно доопределить так, чтобы её график проходил через точку (1,1).

1. Вычислим коэффициент Джинни. Имеем

Т.е. J = 0,06. Таким образом, можно сделать вывод о том, что распределение богатства в обществе нормальное (т. к. J < 0,2).

Зная функцию L(z) найдем другую функцию w(z). Имеем

w(z)=1— L(1 — z).

w(z) = 1 — 2^{1 — z}+1= 2 — 2^{1 — z}

w(1/10) = 2 — 2^9/10 = 0.13

Так что, в этом случае, десятая часть самых бога­тых владеет 13% всего богатства. По функции L(z) определим еще одну функцию:

s(x)=L(1/2+ x) — L(1/2 — x).

S(x) = 2^{1/2 + x} — 1 — 2^{1/2 — x} + 1= 2^{1/2 + x} — 2^{1/2 — x}

S(1/4)= 2^3/4 — 2^1/4 = 0,49 , значит, средний класса в обществе нет.

Распределение богатства в обществе.

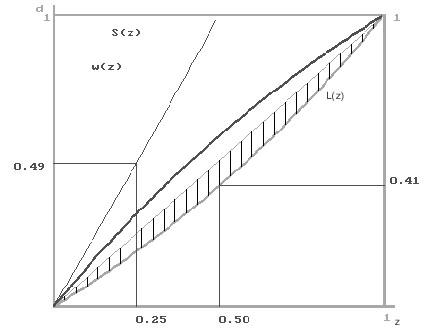
Нужно отметить, что функции d(z), w(z), S(z) не дают представления об абсолютном распределении богатства общества, а лишь о распределении богатства внутри него.

4.2.Распределение общества по получаемому доходу

Пусть F(z) есть доля имеющих месячный доход меньшеzпо отношению ко всем, имеющим какой-нибудь денежный доход (всех таких членов общества назовем налогоплательщиками). ФункциюF(z) вполне правильно трактовать как функцию распределения случайной величиныI— месячный доход случайного налогоплательщика. С.в.Iможно считать непрерывной. ФункцияF(z) может быть интересна налоговой инспекции. Для учебных целей выбраны функцииF(z) , которые вполне могут отличаться от реальной. С помощью функцииF(z) можно найти несколько интересных характеристик общества. Например, средний доход, который находится как интеграл от 0 до бесконечности функцииzdF(z) . Другой подобной характеристикой является коэффициент Рейнбоу, который находится как отношение решений уравненийF(z) = 0.9 иF(z) = 0.1, т.е. этот коэффициент показывает отношение доходов 10% членов общества с самыми высокими доходами к доходам 10% с самыми низкими доходами. Если это отношение превышает 20, то распределение доходов называется несправедливым, иначе — нормальным.

Функция F(z) задана в виде:

Коэффициент Рейнбоу:

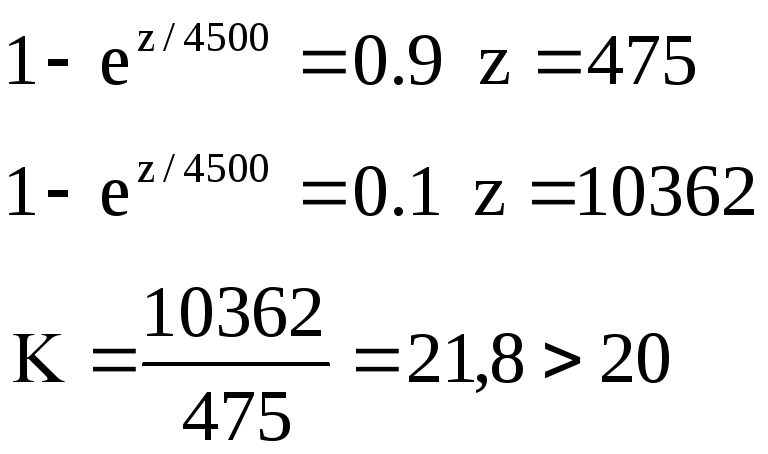
значит распределение доходов несправедливое.

Найдем средний месячный доход:

Найдем размер месячного дохода B_p, который для случайно выбранного налогоплательщика может быть превзойден с вероятностью0,3:

B_p = 5417.9

Функция F(z) даёт довольно хорошее представление об уровне жизни.

Р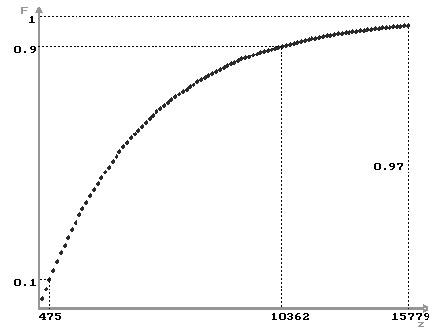аспределение общества по получаемому доходу.