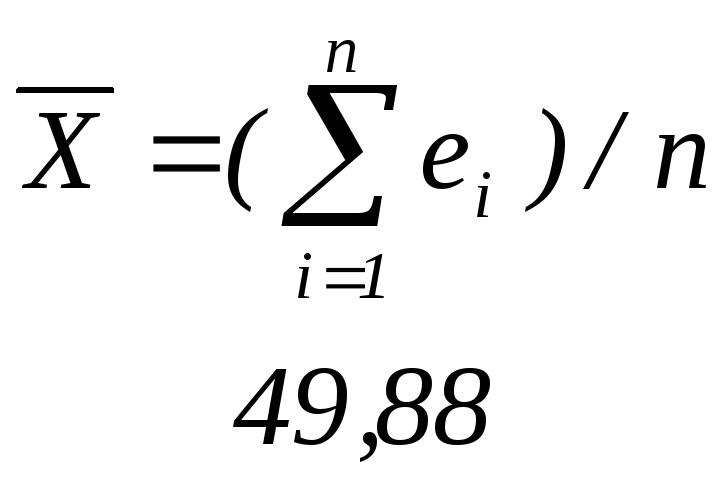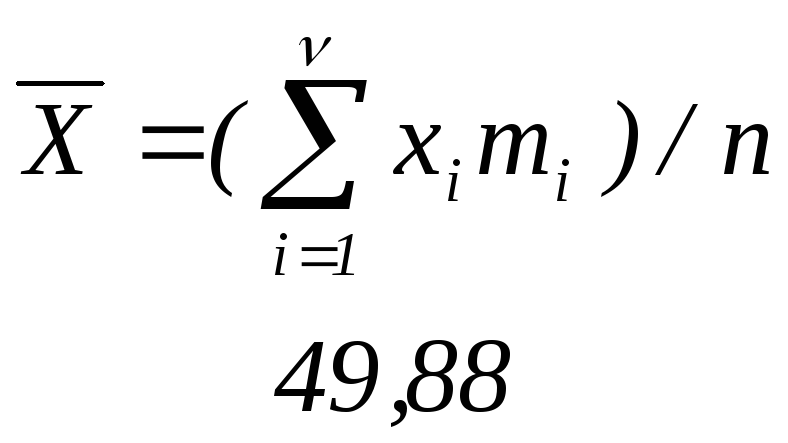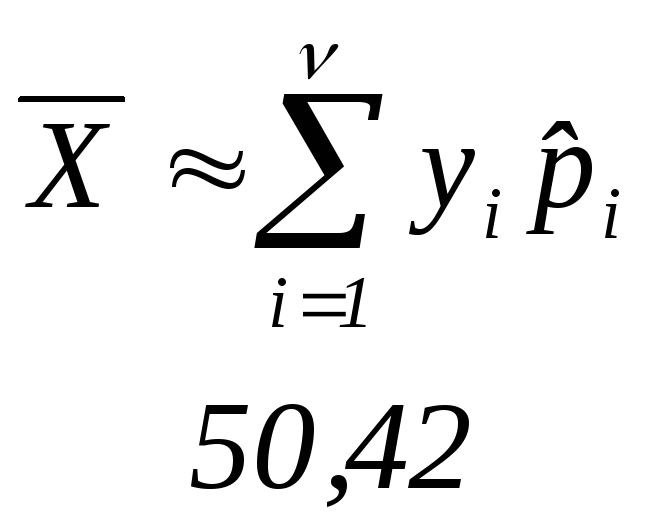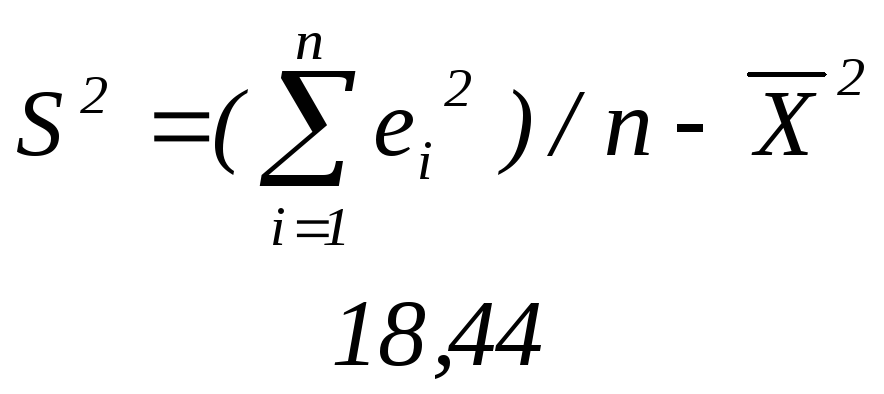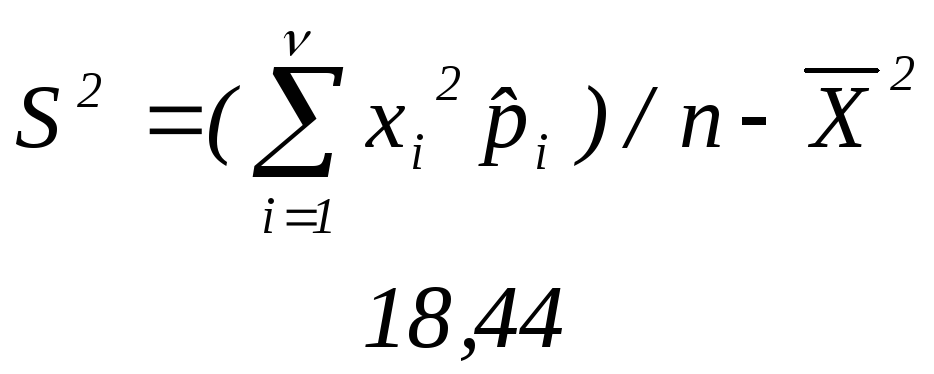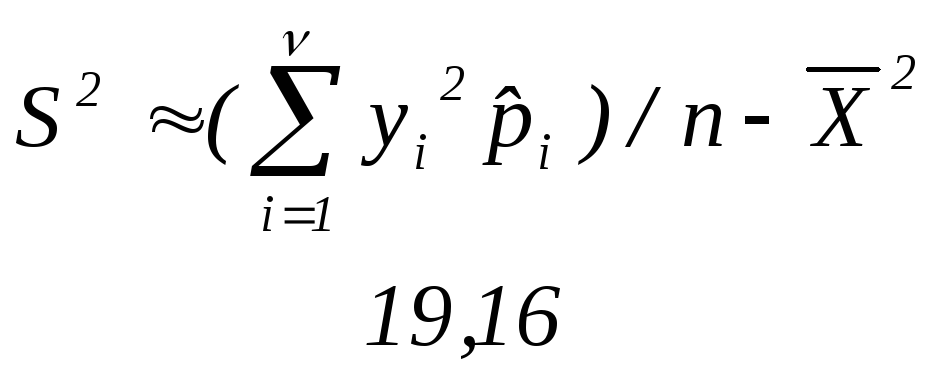2.4. Статистический анализ денежных потоков

Исходные данные для анализа: ежедневные (суммарные) денежные вклады населения, в отделение сбербанка в течение 4-х недель (или аналогичный какой-нибудь денежный поток). Для удобства обработки все числа предполагаются целыми двузначными, что всегда можно сделать округлением и масштабированием.

1-я неделя						2-я неделя						3-я неделя						4-я неделя
1	2	3	4	5	6	1	2	3	4	5	6	1	2	3	4	5	6	1	2	3	4	5	6
56	45	44	46	45	53	55	54	53	49	49	49	49	49	49	52	52	52	52	52	52	40	42	58

Статистические характеристики I:

Денежный поток:

56

45

44

46

45

53

55

54

53

49

49

49

49

49

49

52

52

52

52

52

52

40

42

58

Ранжированный ряд:

40

42

44

45

45

46

49

49

49

49

49

49

52

52

52

52

52

52

53

53

54

55

56

58

Дискретный вариационный ряд:

40	42	44	45	46	49	52	53	54	55	56	58
1	1	1	2	1	6	6	2	1	1	1	1
1/24	1/24	1/24	2/24	1/24	6/24	6/24	2/24	1/24	1/24	1/24	1/24

Многоугольник частот:

Статистические характеристики II:

Интервальный вариационный ряд:

40-42	42-44	44-46	46-48	48-50	50-52	52-54	54-56	56-58	58-60
1/24	1/24	3/24	1/24	6/24	0	8/24	2/24	1/24	1/24

Многоугольник интервальных частостей:

Выборочная функция распределения:

Статистические характеристики III:

	По исходному ряду данных	По дискретному ряду данных	По интервальному ряду данных
Выборочная средняя
Выборочная дисперсия
Выборочное среднеквадратическое отклонение
Несмещенная оценка генеральной дисперсии

§ 3. Модели сотрудничества и конкуренции

3.1. Сотрудничество и конкуренция двух фирм на рынке одного товара

А. Пусть Рассмотрим две фирмы, выпускающие один и тот же товар. Пусть затраты -ой фирмы при выпуске равны (таким образом, есть себестоимость выпуска одной единицы товара). Произведенный обеими фирмами товар поступает на общий рынок. Цена на товар линейно падает в зависимости от поступающего на рынок общего его количества, т.е.,.