
Прикладная математика. Курсовые. / вариант 10 / Вар 10 / Математика 1
.3.doc
-
Задача о “расшивке узких мест”.
Исходные данные:
из задачи 1.1. получили следующие данные
|
|
X5 X4 X1 |
6 28 40 |
0 0 1 |
19/9 2/9 4/9 |
3 -1 1 |
0 1 0 |
1 0 0 |
-7/9 4/9 -1/9 |
1/3 -1/3 1/3 |
|
|
Z |
3340 |
0 |
7 |
4 |
0 |
0 |
9 |
8 |
Задание:
Решить задачу о “расшивке узких мест”.
Решение:
При выполнении оптимальной производственной программы второй и третий ресурсы используются полностью, т.е. образуют “узкие места производства”. Будем их заказывать дополнительно. Пусть Т(0, t2, t3) – вектор дополнительных объемов ресурсов. Так как используются найденные двойственные оценки, то должно выполняться следующее условие:
H + Q-1T ≥ 0.
Задача состоит в том, чтобы найти вектор , максимизирующий суммарный прирост прибыли:
W = 9 t2 + 8 t3
при условии сохранения двойственных оценок ресурсов (и, следовательно, структуры производственной программы), предполагая, что можно надеяться получить дополнительно не более 1/3 первоначального объема ресурса каждого вида
0
 102
102
t2 ≤ 1/3 204
t3 188 ,
причем по смыслу задачи t2 ≥0, t3 ≥ 0.
Следовательно, получаем
6


 1 -7/9 1/3 0
0
1 -7/9 1/3 0
0
28 + 0 4/9 -1/3 • t2 ≥ 0
40 0 -1/9 1/3 t3 0 .
Перемножим матрицы и получим следующую систему неравенств:
-
 7/9t2
+ 1/3t3
≥ -6, -7t2
+ 3t3
≥ -54, (I)
7/9t2
+ 1/3t3
≥ -6, -7t2
+ 3t3
≥ -54, (I)
4/9t2 – 1/3t3 ≥ -28, 4t2 – 3t3 ≥ -252, (II)
-1/9t2 + 1/3t3 ≥ -40, - t2 + 3t3 ≥ -360; (III)
t2 ≤ 204/3, t3 ≤ 188/3, t2 ≤204/3, t3 ≤ 188/3,
t2 ≥ 0, t3 ≥ 0; t2 ≥ 0, t3 ≥ 0.
Решим данную задачу графически.
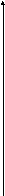
 t3
t3
II
84

 М
М






 188/3
188/3


 I
I



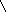

0 54/7 68 t2
Программа “расшивки” имеет вид
t2 = 0, t2 = 242/7 , t3 = 188/3,
и прирост прибыли составит maxW = 9∙242/7+ 8∙188/3 =17062/21 ≈ 812,48 в точке М(242/7,188/3).
