- Область устойчивости двойственных оценок, где

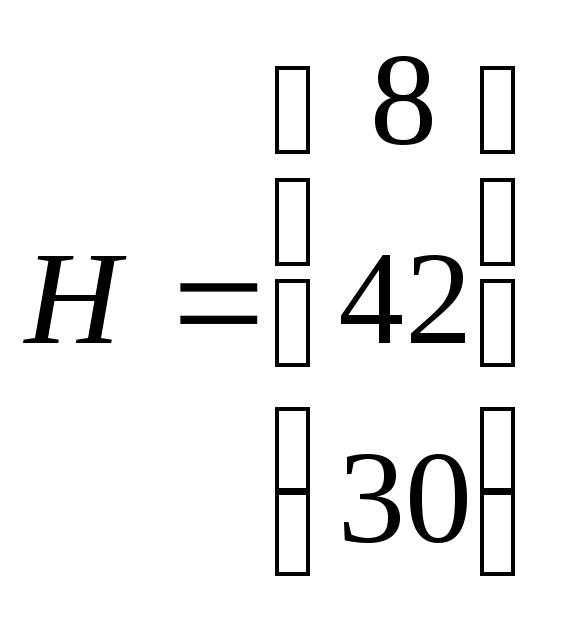- вектор свободных членов системы ограничений из 1-ой задачи

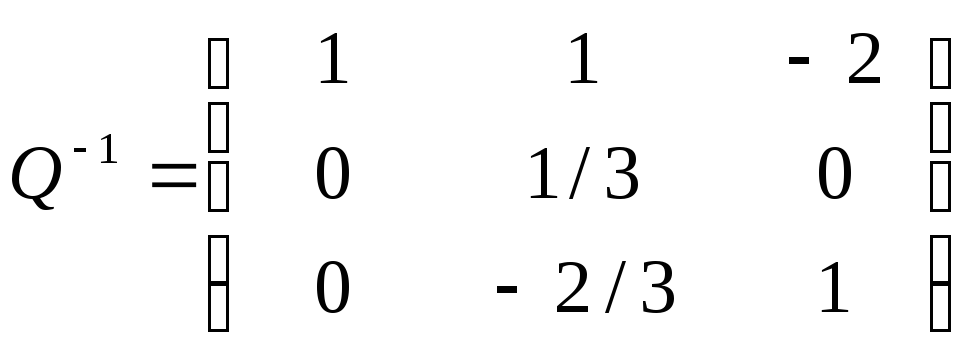- обращённый базис

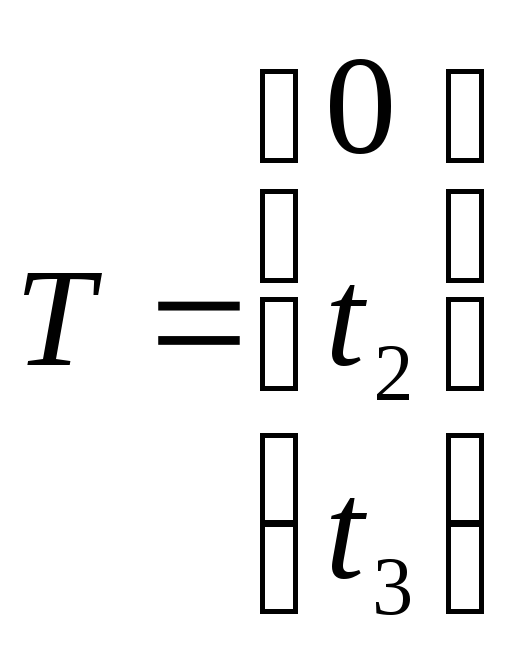- вектор дополнительных объемов ресурсов

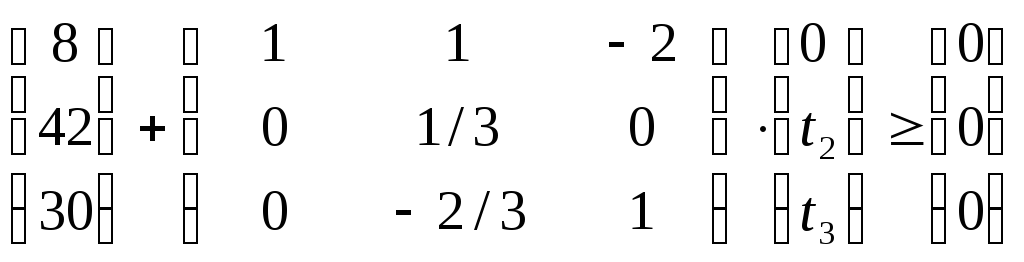
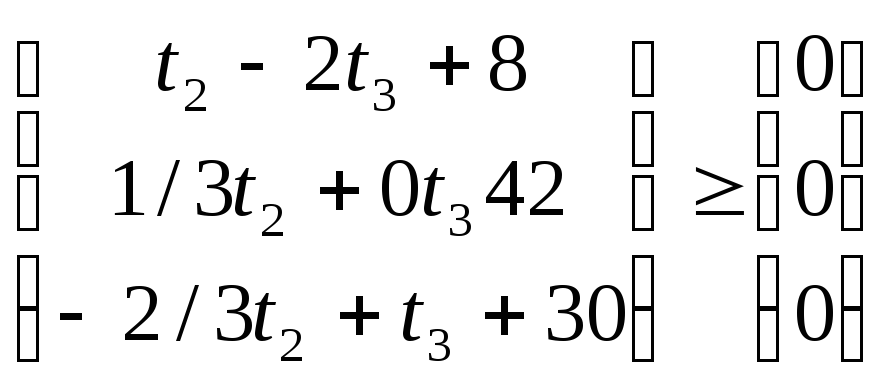
Кроме того, закупки ресурсов не могут превышать трети ресурсов уже находящихся на предприятии:

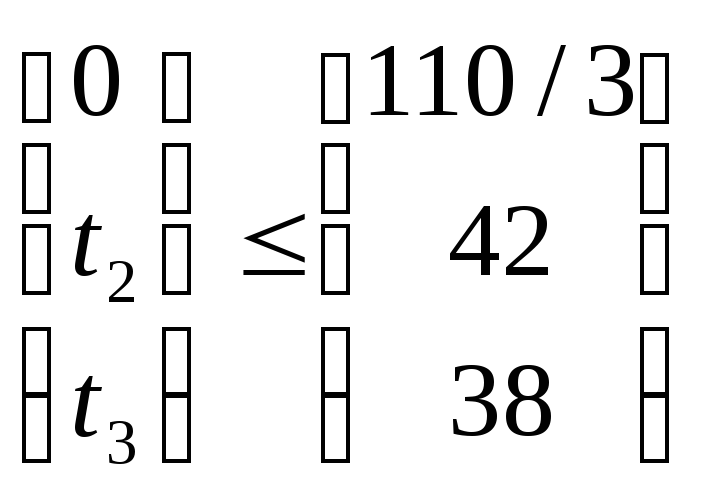
Так как 2-ой и 3-ий ресурсы расходуются полностью, то и больше 0.

Мы получили математическую модель задачи «расшивки узких мест»:

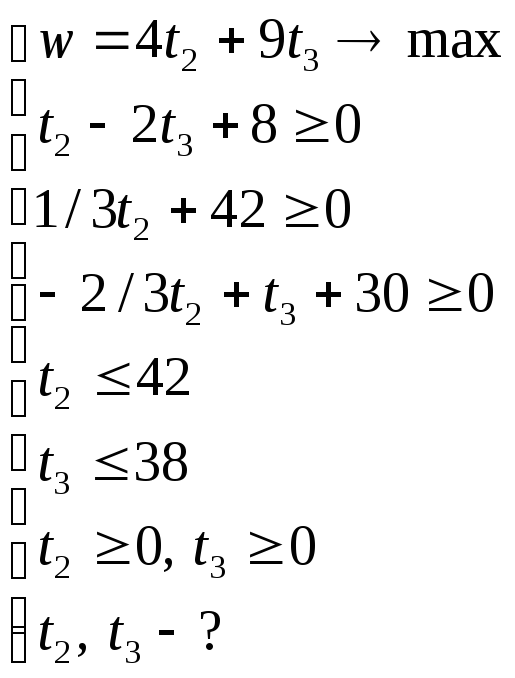
Решим задачу графически:

Так как , то можно исключить из системы:

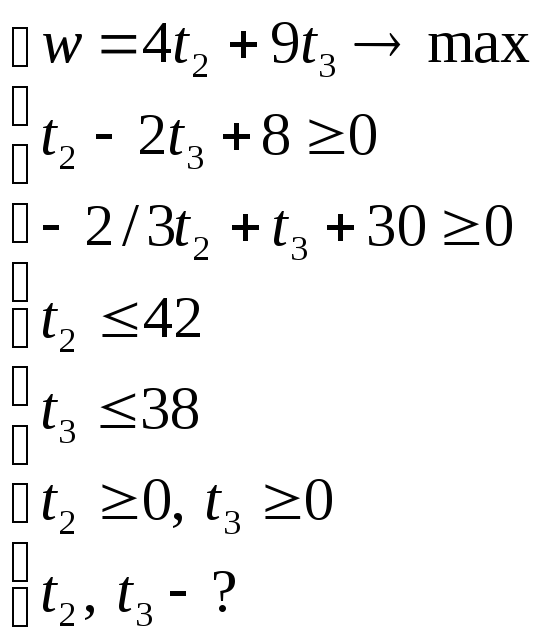
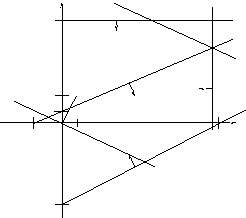
где 1 - , 2 - , 3 - , 4 - 5 – градиент целевой функции , 6 – линия уровня, заштрихованная область – область допустимых решений, т.е. значения и , при которых выполняются ограничения. ОДР образует многоугольник. Передвигая линию уровня по направлению градиента, мы пройдём все вершины многоугольника ОДР. Последняя вершина будет соответствовать максимальному значению целевой функции. В данном случае это точка А с координатами (42;25) ( и ). Область устойчивости находится между и прямыми (двойная штриховка).

Программа расшивки имеет вид: (0, 42, 25), а прирост прибыли составляет

Задание №3

Имеется 3 производителя однородной продукции, имеющие запасы этой продукции 65, 40 и 70 единиц соответственно. Также имеется 4 потребителя данной продукции. Их потребность составляет 30, 58, 32 и 43 единицы соответственно. Транспортная компания заключила контракт с поставщиками и потребителями на вывоз и поставку данной продукции от производителей к потребителям. При перевозке продукции от каждого производителя к каждому потребителю транспортная компания имеет определённые издержки на единицу продукции: 1 у.е. при перевозке от 1-ого производителя к 1-ому потребителю, 3 у.е. - от 1–ого производителя ко 2-ому потребителю, 2 у.е. – от 1-ого к 3-ему, 5 у.е. – от 1-ого к 4-ому, 4 у.е. – от 2-ого к 1-ому, 6 у.е. – от 2-ого ко 2-ому, 5 у.е. – от 2-ого к 3-ему, 9 у.е. – от 2-ого к 4-ому, 2 у.е. – от 3-его к 1-ому, 4 у.е. – от 3-его ко 2-ому, 1 у.е. – от 3-его к 3-ему, 3 у.е. – от 3-его к 4-ому. Так как естественным стремлением транспортной компании является максимизация прибыли, то требуется составить такой план перевозок, чтобы издержки были минимальными.

Можно записать эти издержки на единицу продукции в виде матрицы, где строка издержки при поставке от одного производителя к каждому потребителю, а столбец издержки при поставке к одному потребителю от каждого производителя:

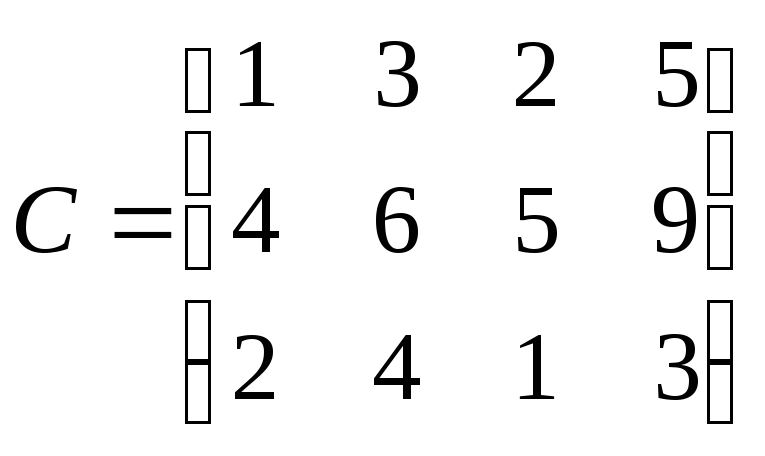
Предложение производителей и спрос потребителей можно записать в виде векторов А и B соответственно:

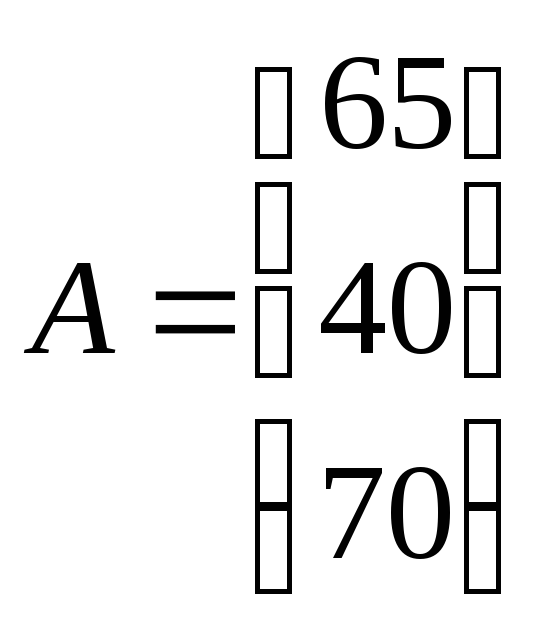и

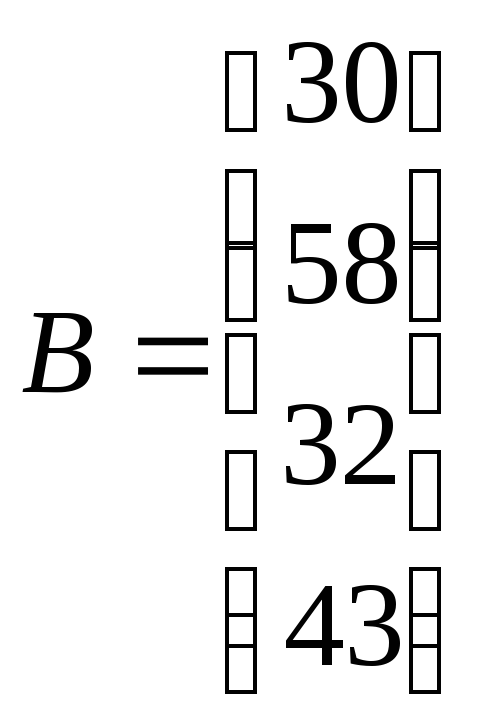
Суммарное предложение не больше суммарного спроса. Для того, чтобы они были равны введём фиктивного потребителя с потреблением равным разнице между предложением и спросом.. Фактически эта потребность будет указывать на количество продукции, которая не будет вывозиться от производителя. Для того, чтобы введение фиктивного потребителя не повлияло на решение, затраты на перевозку единицы продукции к фиктивному потребителю приравняем к 0. В действительности это будет также, так как транспортная компания не будет нести издержки за товар, который она никуда не возит. Тогда вектор В и матрица С будут выглядеть так:

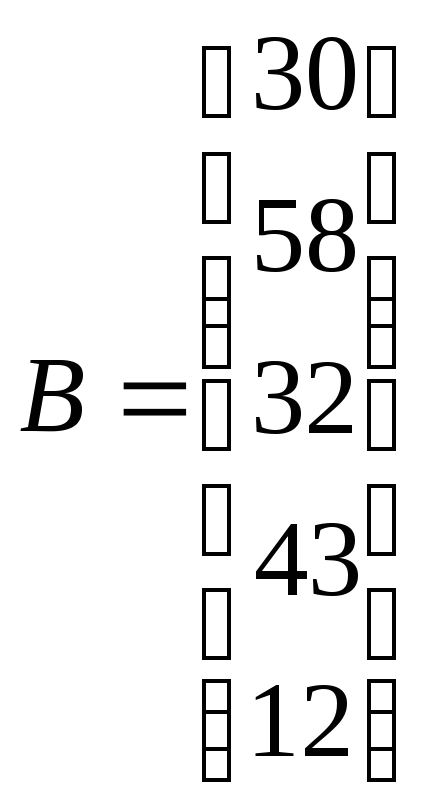и

Мы получили так называемую «замкнутую» задачу.

Обозначим количество перевезённой продукции за x. Таким образом, количество перевезённой продукции от 1-ого производителя к 1-ому потребителю будет , а от 1-ого производителя ко 2-ому потребителю - и т.д. Мы получим матрицу одного размера с С:

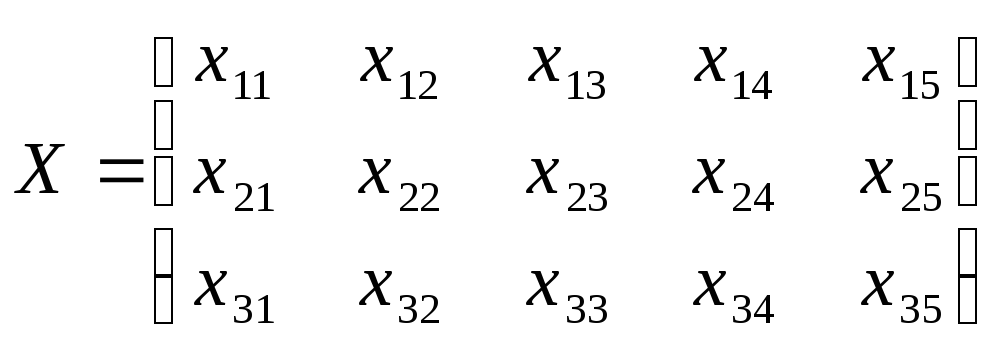
Так как нам требуется найти план перевозок, т.е. такие x, чтобы суммарные издержки были минимальными, то выражение

,

значение которого и есть суммарные издержки (т.е. количество перевезённой продукции помноженное на соответствующие издержки на единицу продукции из матрицы С), должно быть минимальным.

С другой стороны, суммарные перевозки от одного производителя должны быть равны его запасам, а суммарные перевозки к одному потребителю должны быть равны его потреблению:

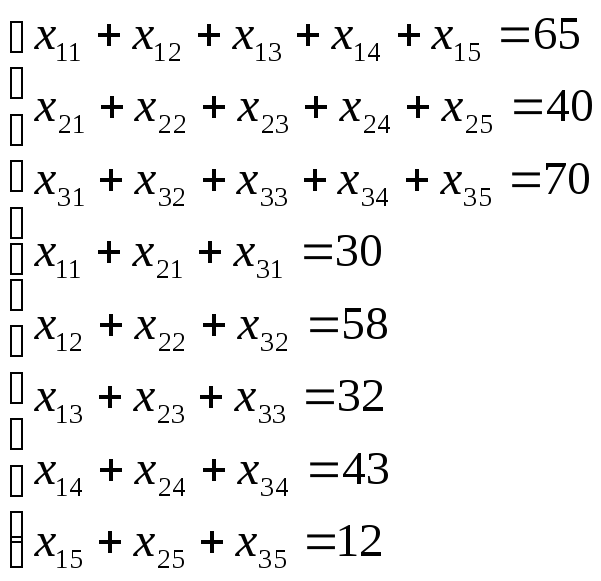
Кроме того, все количество перевозимой продукции по смыслу задачи должно быть положительной.

Итак, математическая модель нашей задачи:

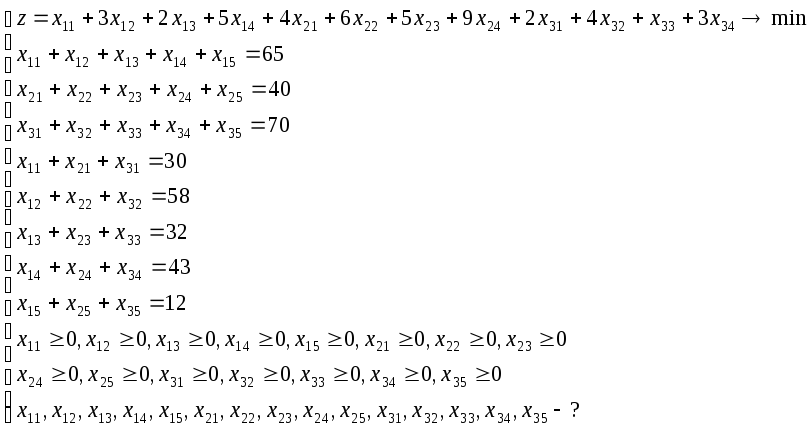
Это задача линейного программирования. Решим её методом потенциалов. Составляется таблица, которая соответствует матрице X. Для решения требуется первое базисное решение. Найдем его с помощью метода минимальных издержек: выбирается 1-ая базисная переменная соответствующая минимальным издержкам, ей присваивается максимально возможное значение; потом выбирается по тому же критерию 2-ая базисная переменная среди оставшихся и т.д.

	30	58	32	43	12
65	30 1	35 3	-- 2	-- 5	-- 0
40	-- 4	23 6	-- 5	5 9	12 0
70	-- 2	-- 4	32 1	38 3	-- 0

где «--» соответствует свободным переменным, а числа в нижнем правом углу ячейки – соответствующим издержкам.

Пусть p и q – двойственные переменные, соответствующие строкам и столбцам таблицы. Если значения x, p и q - допустимые решения соответствующих двойственных задач, то при равенстве целевых функций эти решения – оптимальны. Для того чтобы целевые функции были равны требуется выполнение условий: для базисных переменных и для свободных переменных (). Таким образом, для нашей таблицы получим систему:

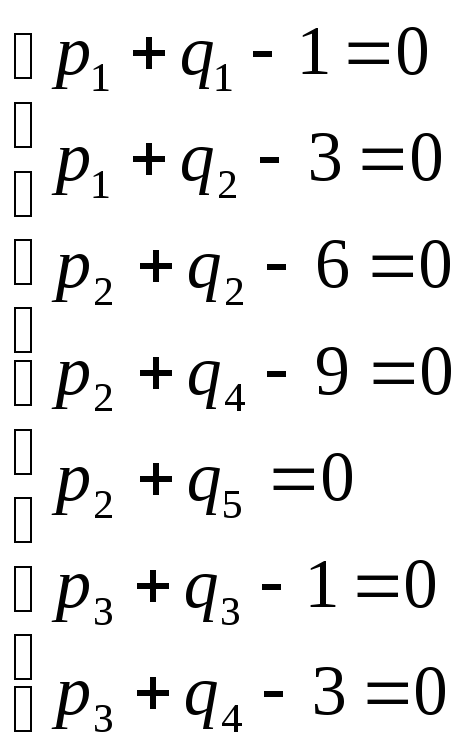
Пусть , тогда - это допустимое решение.

Тогда - решение не оптимально т.к. есть .

Так как решение не оптимально поменяем набор базисных переменных. Для этого выберем ячейку, которой соответствует максимальная симплекс-разница . Для того, чтобы не нарушить равновесия воспользуемся методом циклического пересчёта:

	30	58	32	43	12
65	30 1	35 3	-- 2	-- 5	-- 0
40	-- 4	23 6	+w--5	-w5 9	12 0
70	-- 2	-- 4	-w321	+w383	-- 0

где w=5. Таким образом, сумма в строках и столбцах осталась неизменной, а мы получили новое базисное решение:

	30	58	32	43	12
65	30 1	35 3	-- 2	-- 5	-- 0
40	-- 4	23 6	5 5	-- 9	12 0
70	-- 2	-- 4	27 1	43 3	-- 0

Проверим его на оптимальность:

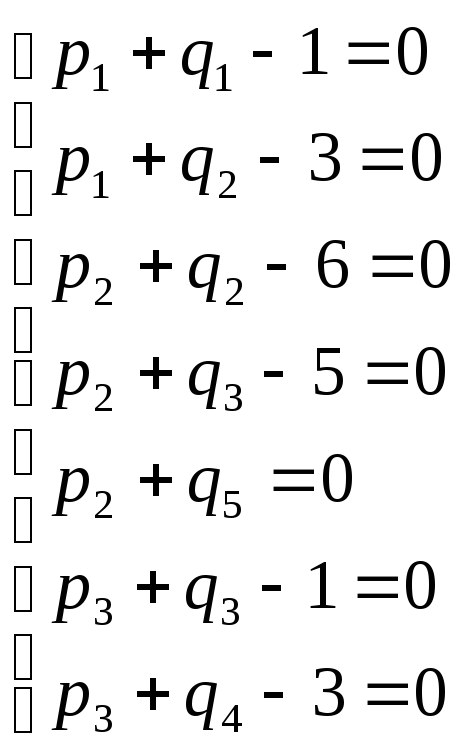
- решение оптимально, так как все симплекс разницы

Ответ: при 12 единицах продукции оставшихся у 2-ого производителя.

13