Задание №2

1

Некое предприятие, использующее те же ресурсы что и предприятие из предыдущей задачи, желает приобрести все эти ресурсы. Оно желает приобрести их по ценам , и соответственно за единицу каждого из трёх ресурсов. Из условий предыдущей задачи нам известны затраты всех 3-х ресурсов для производства для каждого из 4-х видов продукции, количество ресурсов на производстве и прибыль от единицы каждой продукции. Их мы представили в виде матриц и векторов:

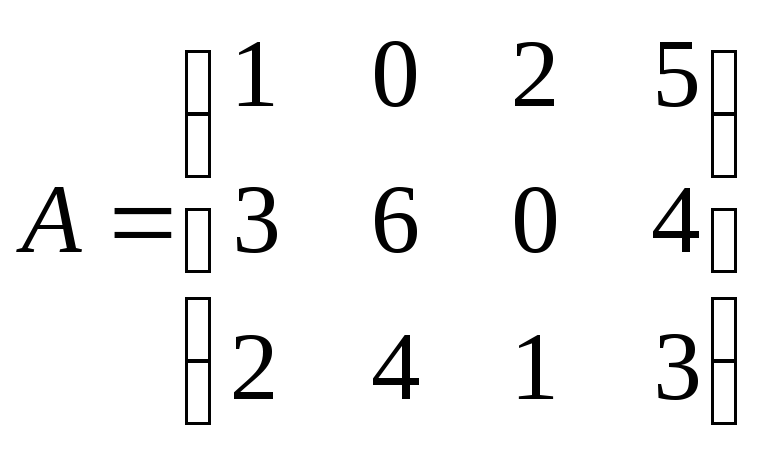
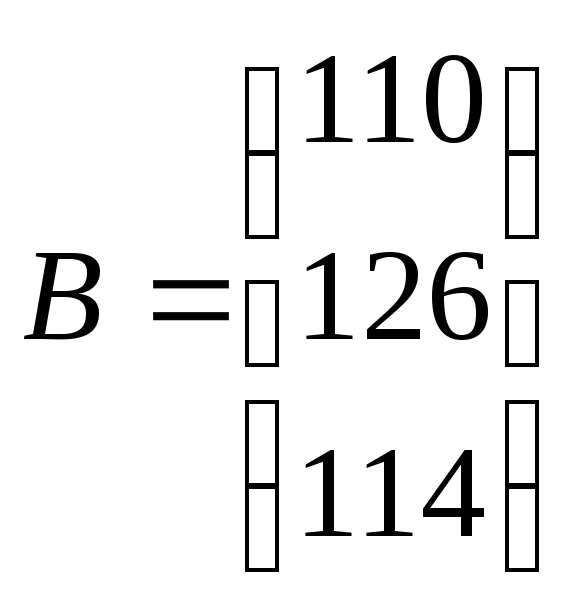
Так как продажа ресурсов должна быть целесообразной, то прибыль от продажи единице каждого вида продукции должна быть меньше, чем прибыль от продажи ресурсов в количестве равном затрате этих ресурсов для производства единицы продукции каждого вида.

Для производства продукции 1-ого вида требуется 1 единица 1-ого ресурса, 3 единицы 2-ого ресурса и 2 единицы 3-его ресурса, что соответствует элементам 1-ого столбца матрица А. Прибыль от продажи продукции 1-ого вида равна 30. Следовательно, для целесообразности продажи ресурсов прибыль от продажи 1 единицы 1-ого ресурса, 3-х единиц 2-ого ресурса и 2-х единиц 3-его ресурса должна быть больше, либо равна 30, т.е. прибыли от продажи продукции 1-ого вида:

Соответственные условия должны выполняться и для продукции других видов. Им соответствуют 2-ой, 3-ий и 4-ый столбцы матрицы А, а также 2-ой, 3-ий и 4-ый элементы матрицы-строки прибыли С:

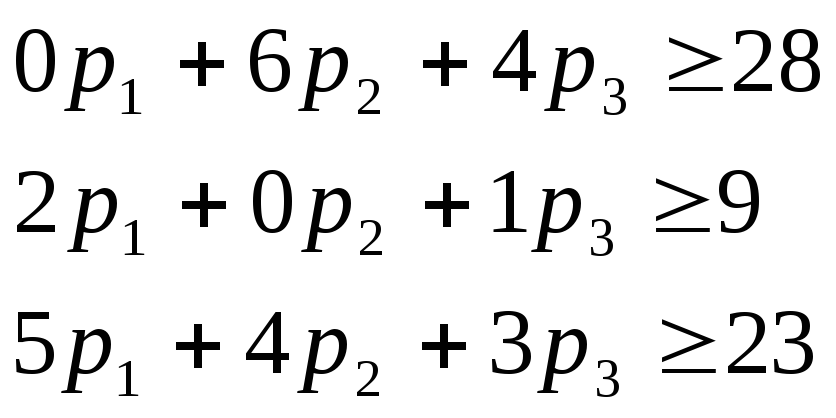
Но при продаже требуется учитывать и интересы покупателя. Естественным желанием покупателя является снижение расходов. Так как предприятие желает закупить весь объём имеющихся ресурсов, то его затраты при ценах , и составят , где коэффициенты при , и - количество имеющихся ресурсов. Таким образом:

Кроме того, так как цены не могут быть отрицательными, то .

Таким образом, для нахождения оптимальной цены продажи ресурсов необходимо решить систему:

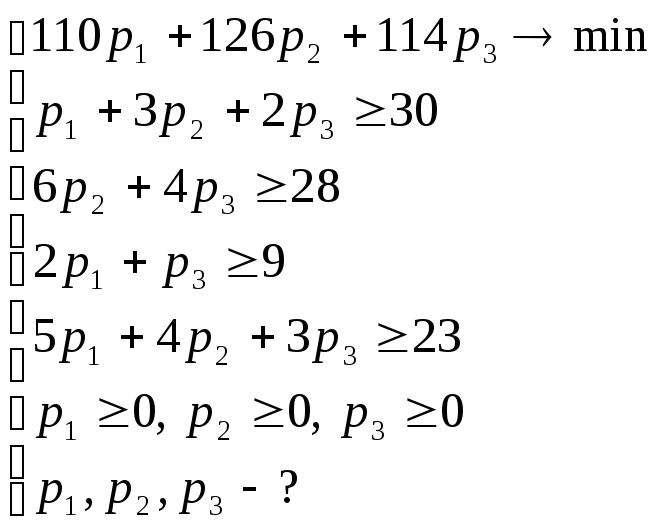
Мы получили задачу двойственную линейной производственной задаче из 1-ого задания. Отсюда, по 2-ой теореме двойственности, при производственной программе и ценах , и , необходимым и достаточным условием оптимальности решений двойственных задач является выполнение условий:

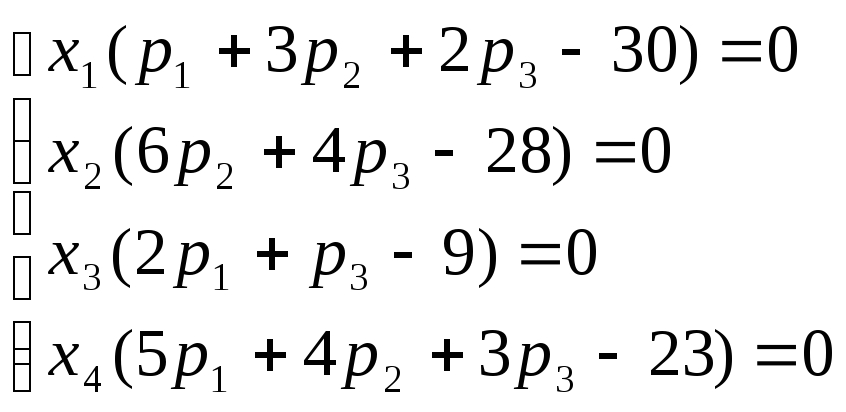
Учитывая, что для линейной производственной задачи оптимальное решение уже найдено (42, 0, 30. 0), подставим эти значения систему:

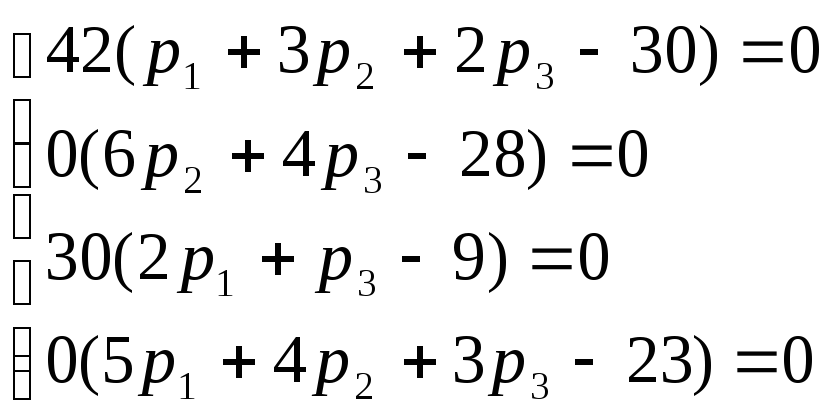
Так как 42 и 30 не равны 0, то мы получим систему:

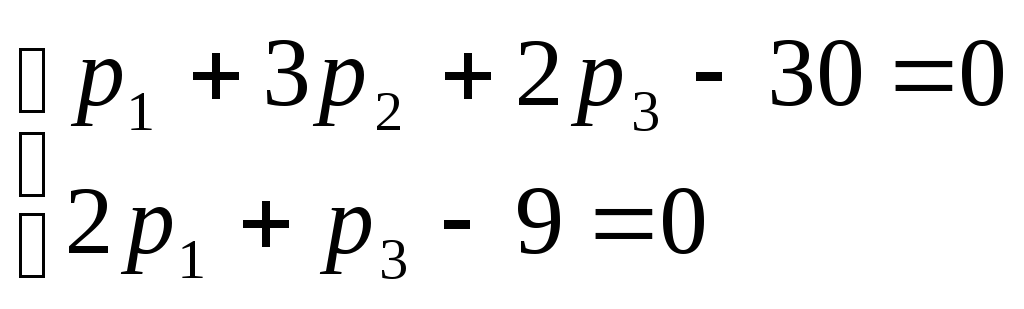
Учитывая, что 1-ый ресурс был избыточным, то, согласно теореме двойственности, его двойственная оценка , получим систему:

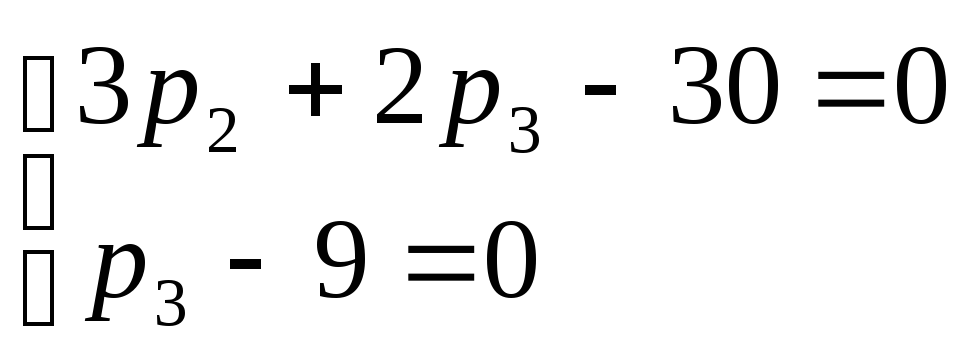
Решив её, мы получим и . Оптимальное решение:

(0, 4, 9)

Данные значения , и являются двойственными оценками соответствующих ресурсов, т.е. оценка единицы 1-ого ресурса равна 0, оценка единицы 2-ого ресурса равна 4, а оценка 3-его ресурса равна 9. Эти оценки являются «теневыми» ценами ресурсов. Экономически они указывают на сколько увеличится прибыль при выполнении оптимальной производственной программы, если количество соответствующего ресурса увеличить на единицу, при неизменном количестве остальных ресурсов.

Используя задачу 1, мы можем найти оценку технологии, т.е. на сколько уменьшится прибыль, если будет произведена 1 единица продукции не по оптимальной программе. Оценки технологий получились в конечной симплексной таблице как коэффициенты при соответствующих x в целевой функции. Таким образом, при производстве единицы 2-ой продукции прибыль упадёт на 32, а для 4-ой продукции падение составит 20.

2.

При выполнении оптимальной производственной программы из задания 1 2-ой и 3-ий ресурс расходуются полностью, они образовывают «узкие места» производства. Для увеличения прибыли требуется закупить дополнительно данные ресурсы в количестве и . Закупки 1-ого ресурса не требуются, так как этот ресурс избыточен.

Предыдущей задаче были найдены двойственные оценки ресурсов. Они показывают насколько увеличится прибыль, если увеличить количество ресурса на единицу. Таким образом, общая прибыль от использования дополнительных ресурсов в количестве и будет равна . Так как требуется максимально увеличить прибыль то:

Оптимальное решение исходной задачи можно представить в виде:

Новое решение будет иметь вид: Если оно допустимо, то требуется. Чтобы структура производства не поменялась, т.е . Отсюда: