§ 1. Оптимальное производственное планирование
1.1. Линейная задача производственного планирования
Задача линейного оптимального планирования – один из важнейших математических инструментов, используемых в экономике. Рассмотрим предприятие, которое из m видов ресурсов производит n видов продукции. Известны нормы расхода a[i,j] – количество единиц i-го ресурса, расходуемое на производство одной единицы j-го вида продукции. Известны запасы ресурсов – i-го ресурса имеется b[i], известны удельные прибыли c[j] – прибыли от реализации одной единицы j-го вида продукции. План производства X=(x[1],..., x[n]) называется допустимым, если имеющихся ресурсов для него достаточно. Рассматриваемая задача состоит в нахождении допустимого плана, дающего максимальную прибыль из всех допустимых планов. Такой план называется оптимальным. Симплекс-метод является наиболее мощным и распространенным методом решения подобных задач, называемых задачами линейного программирования – ЛП.
З
аданы
удельные прибыли, нормы расхода и запасы
ресурсов и компьютер решает поставленную
задачу симплекс-методом.
|
42 |
28 |
17 |
19 |
|
|
5 |
2 |
4 |
1 |
132 |
|
3 |
4 |
0 |
6 |
124 |
|
4 |
2 |
54 |
4 |
117 |
Обозначим x1, x2, x3, x4 – число единиц 1-й, 2-й, 3-й, 4-й продукции, которые планируем произвести. При этом можно использовать только имеющиеся запасы ресурсов. Целью является получение максимальной прибыли. Получаем следующую математическую модель оптимального планирования:
P(x1,x2,x3,x4)=42∙x1+28∙x2+17∙x3+19∙x4→max
5∙x1+2∙x2+4∙x3+1∙x4≤132
3∙x1+4∙x2+0∙x3+6∙x4≤124
4∙x1+2∙x2+54∙x3+4∙x4≤117
x1,x2,x3,x4≥0
Для решения полученной задачи в каждое неравенство добавим неотрицательную переменную. После этого неравенства превратятся в равенства, в силу этого добавляемые переменные называются балансовыми. Получается задача ЛП на максимум, все переменные неотрицательны, все ограничения есть равенства и есть базисный набор переменных: x5 – в 1-м равенстве, x6 – во 2-м и x7 – в 3-м . Теперь можно запускать симплекс-метод.
P(x1 –x7)=42∙x1+28∙x2+17∙x3+19∙x4+0∙x5+0∙x6+0∙x7→max
5∙x1+2∙x2+4∙x3+1∙x4+1∙x5=132
3∙x1+4∙x2+0∙x3+6∙x4+ 1∙x6=124
4∙x1+2∙x2+54∙x3+4∙x4+ 1∙x7=117
x1 –x7≥0
Таблица №1
|
|
|
36 |
14 |
25 |
50 |
0 |
0 |
0 |
| |
|
С |
Б |
Н |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
|
|
0 |
x5 |
132 |
5 |
2 |
4 |
1 |
1 |
0 |
0 |
26.4 |
|
0 |
x6 |
124 |
3 |
4 |
0 |
6 |
0 |
1 |
0 |
41.33 |
|
0 |
x7 |
117 |
4 |
2 |
54 |
4 |
0 |
0 |
1 |
29.25 |
|
|
P |
0 |
-42 |
-28 |
-17 |
-19 |
0 |
0 |
0 |
|
Если все оценочные коэффициенты (зеленый цвет) неотрицательны, то получено оптимальное решение: базисные переменные равны свободным членам, остальные равны 0, максимум целевой функции указан правее буквы P. Если же есть отрицательный оценочный коэффициент, то находят самый малый из них. Если в столбце коэффициентов над ним (голубой цвет) нет положительных, то задача не имеет решения. Задача оптимального планирования не может быть таковой, поэтому ищут минимальное отношение свободных членов к положительным элементам указанного столбца (это отношение указано справа от таблицы голубым цветом, а минимальное отношение – красным). В пересечении двух голубых строки и столбца получаем разрешающий элемент (красный цвет) и затем строим новую таблицу.
Таблица №2
|
|
|
|
42 |
28 |
17 |
19 |
0 |
0 |
0 |
|
|
С |
Б |
Н |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
X7 |
|
|
0 |
X1 |
26.40 |
1.00 |
0.40 |
0.80 |
0.20 |
0.20 |
0 |
0 |
66 |
|
0 |
x6 |
44.80 |
0 |
2.80 |
-2.4 |
5.40 |
-0.6 |
1 |
0 |
16 |
|
50 |
X7 |
11.40 |
0 |
0.40 |
50.8 |
3.20 |
-0.8 |
0 |
1 |
28.5 |
|
|
P |
1108.8 |
0 |
-11.2 |
16.6 |
-10.6 |
8.40 |
0 |
0 |
|
Если есть отрицательные оценочные коэффициенты (зеленый цвет), то проделываем то же самое еще раз (см. выше).
Таблица №3
|
|
|
|
42 |
28 |
17 |
19 |
0 |
0 |
0 |
| |||||||||||||||||||||
|
С |
Б |
Н |
x1 |
x2 |
x3 |
x4 |
x5 |
X6 |
X7 |
|
| ||||||||||||||||||||
|
36 |
x1 |
20 |
1 |
-0 |
1.14 |
-0.57 |
0.29 |
-0.14 |
0 |
| |||||||||||||||||||||
|
0 |
X2 |
16 |
0 |
1 |
-0.86 |
1.93 |
-0.21 |
0.36 |
0 |
16 | |||||||||||||||||||||
|
50 |
X7 |
5 |
0 |
-0 |
51.14 |
2.43 |
-0.71 |
-0.14 |
1 |
| |||||||||||||||||||||
|
|
P |
1288 |
0 |
-0 |
7 |
11 |
6 |
4 |
0 |
| |||||||||||||||||||||
Оптимальное решение: x1=20, x2=16, x7=5, все остальные переменные равны 0; максимум целевой функции равен 1288; значение переменной с номером i большим 4 есть остаток (i-4)-го ресурса.
Так как все оценочные коэффициенты (зеленый цвет) неотрицательны, то получено оптимальное решение: базисные переменные равны свободным членам, остальные равны 0, максимум целевой функции указан правее буквы P. Выше выписан ответ.
1.2. Двойственная задача линейного программирования
Задача линейного оптимального планирования – исходная в своей паре симметричных двойственных задач. Вообще же другая задача в двойственной паре строится так:
меняется тип экстремума целевой функции (max на min и наоборот);
коэффициенты целевой функции одной задачи становятся свободными членами другой задачи;
свободные члены одной задачи становятся коэффициентами целевой функции двойственной задачи;
тип неравенств меняется ( <= на => и наоборот);
каждый столбец одной задачи порождает строку ограничений другой задачи и наоборот.
В матрично-векторном виде обе задачи выглядят так:
|
Исходная задача |
Двойственная задача |
|
CX→max AX≤B,X≥0 |
YB→min YA≥B, X≥0 |
|
P=42∙x1+28∙x2+17∙x3+19∙x4→max 5∙x1+2∙x2+4∙x3+1∙x4 ≤132 3∙x1+4∙x2+0∙x3+6∙x4 ≤124 4∙x1+2∙x2+54∙x3+4∙x4 ≤117 x1, x2, x3, x4 ≥0
|
S=132∙y1+124∙y2+117∙y3→min 5∙y1+3∙y2+4∙y3 ≥42 2∙y1+4∙y2+2∙y3 ≥28 4∙y1+0∙y2+54∙y3 ≥17 1∙y1+6∙y2+4∙y3 ≥19 y1, y2, y3 ≥0 |
Решение полученной задачи легко найти с помощью второй основной теоремы двойственности, согласно которой для оптимальных решений X(x1,x2,x3,x4) иY(y1,y2,y3) пары двойственных задач необходимо и достаточно выполнение условий:
-
x1∙(5∙y1+3∙y2+4∙y3-42)=0,
x2∙(2∙y1+4∙y2+2∙y3-28)=0,
x3∙(4∙y1+0∙y2+54∙y3-17)=0,
x4∙(1∙y1+6∙y2+4∙y3-19)=0.
y1∙(5∙x1+2∙x2+4∙x3+1∙x4-132)=0,
y2∙(3∙x1+4∙x2+0∙x3+6∙x4-124)=0,
y3∙(4∙x1+2∙x2+54∙x3+4∙x4-117)=0.
Ранее было найдено, что в решении исходной задачи x1>0,x2>0. Поэтому:
5∙y1+3∙y2+4∙y3-42=0,
2∙y1+4∙y2+2∙y3-28=0.
Если же учесть, что третий ресурс был избыточным и, согласно той же теореме двойственности, его двойственная оценка равна нулю y3=0, то приходим к системе уравнений:
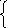5 y1+3 y2=42
2 y1+ 4 y2=28
Таким образом, получили двойственные оценки ресурсовy1=6,y2=4,y3=0, причем общая оценка всех ресурсов равна 1288.
Заметим, что решение содержалось в последней строке симплексной таблицы исходной задачи. Очень важен экономический смысл всех элементов этой строки. Например, двойственная оценка третьего ресурса y2=4 показывает, что добавление одной единицы третьего ресурса обеспечит прирост прибыли в 4 единицы, а оценка третьей технологии ∆3=7 показывает, что если произвести одну единицу продукции 3-го вида (она не входит в оптимальную производственную программу), то прибыль уменьшится на 7 единиц.
1.3. Расшивка узких мест
Таблица №3
-
42
28
17
19
0
0
0
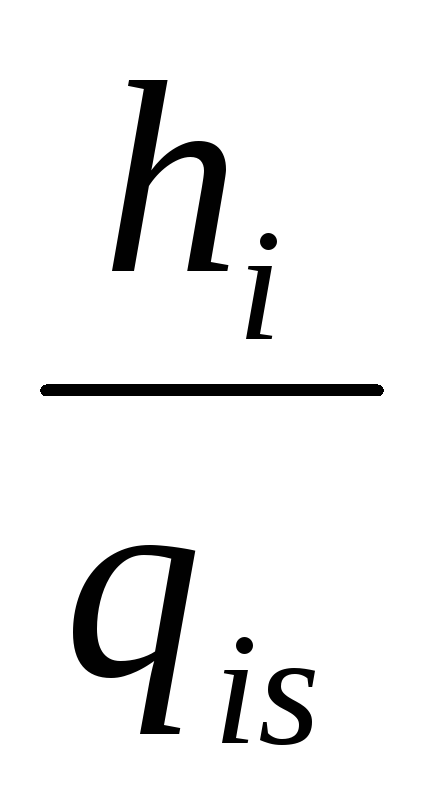
С
Б
Н
x1
x2
x3
x4
x5
x6
x7
42
x1
20
1
0
1.14
-0.57
0.29
-0.14
0
28
X2
16
0
1
-0.86
1.93
-0.21
0.36
0
0
X7
5
0
0
51.14
2.43
-0.71
-0.14
1
P
1288
0
0
7
11
6
4
0
При выполнении
оптимальной производственной программы
первый и второй ресурсы используются
полностью, т.е. образуют «узкие места
производства». Будем их заказывать
дополнительно. Пусть
– вектор дополнительных объемов
ресурсов. Так как мы будем использовать
найденные двойственные оценки ресурсов,
то должно выполняться условие
,
где Н – значения базисных переменных
в последней симплексной таблице, аQ-1– обращенный базис, который образуют
столбцы при балансовых переменных в
этой таблице. Задача состоит в том, чтобы
найти вектор
,
максимизирующий суммарный рост прибыли
(1)
при условии сохранения двойственных оценок ресурсов (и, следовательно, ассортимента выпускаемой продукции)
(2)
предполагая, что
можно надеяться получить дополнительно
не более
первоначального объема ресурса каждого
вида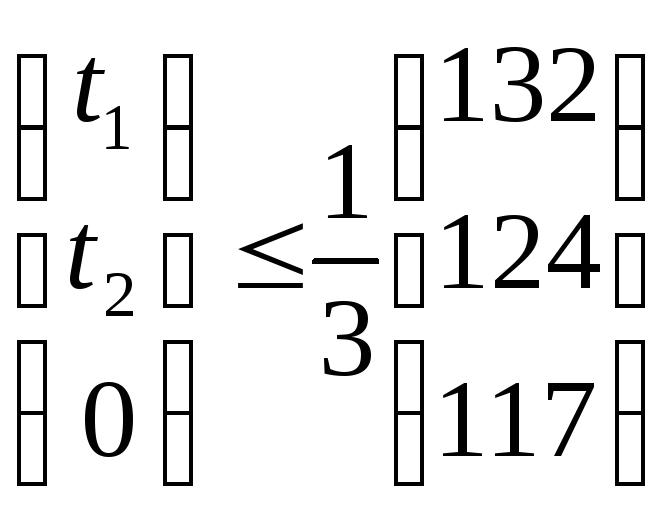
(3)
причем по смыслу
задачи
,
(4)
Переписав неравенства
(2) и (3) в виде:
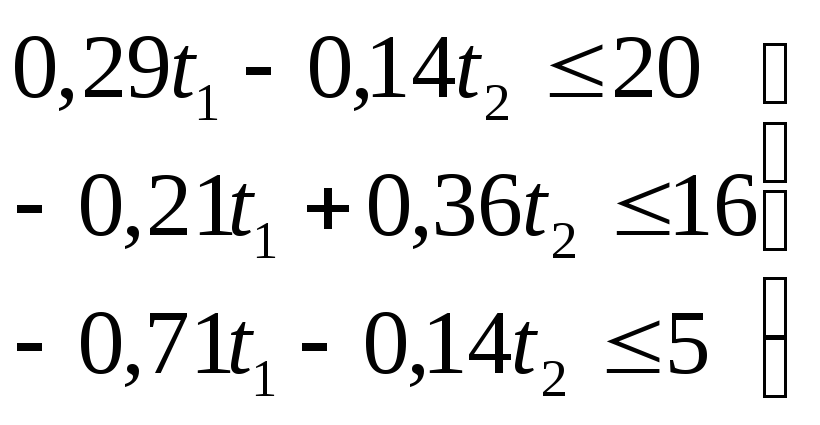(5)
;
(6)
приходим к задаче ЛП: максимизировать (1) при условиях (5), (6) и (4).
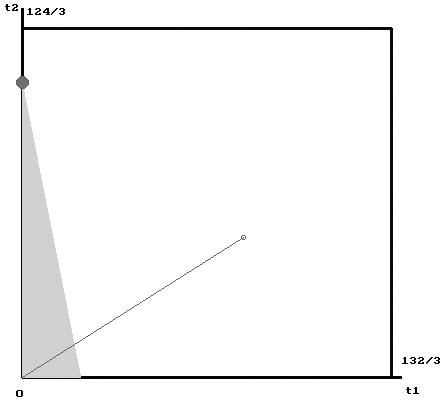
Эту задачу легко решить графически: см. рис. Допустимое множество закрашено серым цветом. Программа «расшивки» имеет вид:
Ответ:
максимальный прирост прибыли составитmaxW=
1.4. Задача о комплектном плане
Задачу ЛП с двумя переменными можно решить графически. Возьмем на плоскости систему координат: ось OX1 направим горизонтально и вправо, ось OX2 – вертикально и вверх. Каждое ограничение задачи, раз оно линейное нестрогое неравенство, графически изображается полуплоскостью, граничная прямая которой соответствует уже не неравенству, а равенству. Допустимое множество задачи является пересечением всех этих полуплоскостей и есть выпуклый многоугольник.
Вторая из двух основных теорем ЛП гласит: Если экстремум целевой функции достигается на допустимом множестве, то функция принимает его в какой-то вершине многоугольника – допустимого множества. Исходя из этой теоремы, найти искомый экстремум можно просто перебрав вершины многоугольника и определив ту, в которой значение функции экстремально. Чаще делают по-другому: строят линию уровня целевой функции и двигают ее параллельно в направлении экстремума, стараясь уловить последнюю точку пересечения линии с допустимым множеством. Зададим задачу ЛП с тремя ограничениями и четырьмя переменными, затем зададим выражения x3 и x4 через x1 и x2 . Теперь переменных осталось две и задача может быть решена графически.
|
42 |
28 |
19 |
17 |
|
|
5 |
2 |
4 |
1 |
132 |
|
3 |
4 |
0 |
6 |
124 |
|
4 |
2 |
54 |
4 |
117 |
Предположим, что в линейной производственной задаче продукция производится комплектно: продукции 3-го вида надо произвести в 2 раза больше, чем 1-го, а 4-го столько же, сколько и 2-го вида продукции. Т.е. имеем соотношения x3=2x1 иx4=x2.
-
76
123
13
7
132
3
34
124
112
22
117
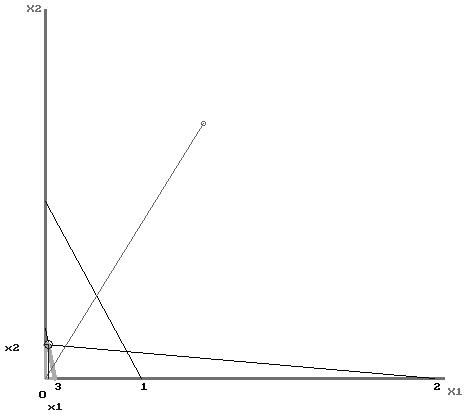
P=76x1+123x2→max
13x1+7x2≤132 (1)
3x1+34x2≤124 (2)
112x1+22x2≤117 (3)
Искомая точка находится как решение системы:
Ответ:x1=0,33;x2=3,62;maxP=470,35.
1.5. Оптимальное распределение инвестиций
Эта задача решается с помощью динамического программирования.
Динамическое программирование – это вычислительный метод для решения задач управления определенной структуры. Данная задача с nпеременными представляется как многошаговый процесс принятия решений. На каждом шаге определяется экстремум функции только от одной переменной.
Знакомство с методом динамического программирования проще всего начать с рассмотрения нелинейной задачи распределения ресурсов между предприятиями одного производственного объединения или отрасли. Для определенности можно считать, что речь идет о распределении капитальных вложений (инвестиций).
Предположим, что указано nпунктов, где требуется построить или реконструировать предприятия одной отрасли, для чего выделеноbрублей. Обозначим черезfi(xi) прирост мощности или прибыли наj-м предприятии, если оно получитxiрублей капитальных вложений. Требуется найти такое распределение (x1,x2,...,xn) капитальных вложений между предприятиями, которое максимизирует суммарный прирост мощности или прибылиz=f1(x1)+f2(x2)+...+fn(xn), при ограничении по общей сумме капитальных вложенийx1+x2+...+xn=b, причем будем считать, что все переменныеxjпринимают только целые неотрицательные значенияxj=0, или 1, или 2, или 3, ...
Функции fj(xj) мы считаем заданными, заметив, что их определение – довольно трудоемкая экономическая задача.
Воспользуемся методом динамического программирования для решения этой задачи. Введем параметр состояния и определим функцию состояния. За параметр состояния ξ примем количество рублей, выделяемых нескольким предприятиям, а функцию состояния Fk(ξ) определим как максимальную прибыль на первыхkпредприятиях, если они вместе получают ξ рублей. Параметр ξ может изменяться от 0 доb. Если из ξ рублейk-ое предприятие получитxkрублей, то каково бы ни было это значение, остальные ξ-xkрублей естественно распределить между предприятиями от первого до (k-1)-го так, чтобы была получена максимальная прибыльFk-1(ξ-xk). Тогда прибыльkпредприятий будет равнаfk(xk)+Fk-1(ξ-xk). Надо выбрать такое значениеxkмежду 0 и ξ, чтобы эта сумма была максимальной, и мы приходим к рекуррентному соотношению:
Fk(ξ)=max{fk(xk)+Fk-1(ξ-xk)}
0≤xk≤ ξ
для k=2,3,4,...,n. Если же k=1, то F1(ξ)=f1(ξ). (при условии, что функция f1 возрастающая).
Пусть 4 фирмы образуют объединение. Рассмотрим задачу распределения инвестиций в размере 700 тыс. рублей по этим 4 фирмам. Размер инвестиций пусть будет кратен 100 тыс. рублей. Эффект от направления i-й фирме инвестиций в размере m (сотен тыс. рублей) выражается функцией fi(m). Приходим к задаче:
f1(x1)+f2(x2)+f3(x3)+f4(x4)→max,
x1+x2+x3+x4≤7,
x1, x2, x3, x4≥0,
где xi – пока еще неизвестный размер инвестиций i-й фирме. Эта задача решается методом динамического программирования: последовательно ищется оптимальное распределение для k=2,3 и 4 фирм. Пусть первым двум фирмам выделено m инвестиций, обозначим z2(m) величину инвестиций 2-й фирме, при которой сумма f2(z2(j))+f1(m-z2(100j)), 0≤j≤m максимальна, саму эту максимальную величину обозначим F2(m). Далее действуем также: находим функции z3 и F3 и т.д. На k-ом шаге для нахождения Fk(m)) используем основное рекуррентное соотношение: Fk(m)=max{fk(j)+Fk-1(m-100j):0<=j<=7}.
|
xj |
0 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
|
f1(x1) |
0 |
28 |
42 |
51 |
57 |
61 |
64 |
66 |
|
f2(x2) |
0 |
5 |
20 |
29 |
36 |
41 |
45 |
47 |
|
f3(x3) |
0 |
8 |
26 |
37 |
47 |
53 |
58 |
61 |
|
f4(x4) |
0 |
22 |
37 |
49 |
59 |
68 |
76 |
82 |
Прежде
всего, заполняем таблицу №1. Значения
f2(x2) складываем
со значениямиF1(ξ-x2)=f1(ξ-x2)
и на каждой северо-восточной диагонали
находим наибольшее число, которое
отмечаем и указываем соответствующее
значение
=100*z2.
Таблица №1
|
|
ξ-x2 |
0 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
|
x2 |
|
0 |
28 |
42 |
51 |
57 |
61 |
64 |
66 |
|
0 |
0 |
0 |
28 |
42 |
51 |
57 |
61 |
64 |
66 |
|
100 |
5 |
5 |
33 |
47 |
56 |
62 |
66 |
69 |
|
|
200 |
20 |
20 |
48 |
62 |
71 |
77 |
81 |
|
|
|
300 |
29 |
29 |
57 |
71 |
80 |
86 |
|
|
|
|
400 |
36 |
36 |
64 |
78 |
87 |
|
|
|
|
|
500 |
41 |
41 |
69 |
83 |
|
|
|
|
|
|
600 |
45 |
45 |
73 |
|
|
|
|
|
|
|
700 |
47 |
47 |
|
|
|
|
|
|
|
Красным цветом обозначен максимальный суммарный эффект от выделения соответствующего размера инвестиций 2 предприятиям.
|
ξ |
0 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
|
F2(ξ) |
0 |
28 |
42 |
51 |
62 |
71 |
80 |
87 |
|
z2 |
0 |
0 |
0 |
0 |
2 |
2 |
3 |
4 |
Таблица №2
|
|
ξ-x3 |
0 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
|
x3 |
|
0 |
28 |
42 |
51 |
62 |
71 |
80 |
87 |
|
0 |
0 |
0 |
28 |
42 |
51 |
62 |
71 |
80 |
87 |
|
100 |
8 |
8 |
36 |
50 |
59 |
70 |
79 |
88 |
|
|
200 |
26 |
26 |
54 |
68 |
77 |
88 |
97 |
|
|
|
300 |
37 |
37 |
65 |
79 |
88 |
99 |
|
|
|
|
400 |
47 |
47 |
75 |
89 |
98 |
|
|
|
|
|
500 |
53 |
53 |
81 |
95 |
|
|
|
|
|
|
600 |
58 |
58 |
86 |
|
|
|
|
|
|
|
700 |
61 |
61 |
|
|
|
|
|
|
|
Красным цветом обозначен максимальный суммарный эффект от выделения соответствующего размера инвестиций 3 предприятиям.
|
ξ |
0 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
|
F3(ξ) |
0 |
28 |
42 |
54 |
68 |
79 |
89 |
99 |
|
z3 |
0 |
0 |
0 |
2 |
2 |
3 |
4 |
3 |
Таблица №3
|
|
ξ-x4 |
0 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
|
x4 |
|
0 |
28 |
42 |
54 |
68 |
79 |
89 |
99 |
|
0 |
0 |
0 |
28 |
42 |
54 |
68 |
79 |
89 |
99 |
|
100 |
22 |
22 |
50 |
64 |
76 |
90 |
101 |
111 |
|
|
200 |
37 |
37 |
65 |
79 |
91 |
105 |
116 |
|
|
|
300 |
49 |
49 |
77 |
91 |
103 |
117 |
|
|
|
|
400 |
59 |
59 |
87 |
101 |
113 |
|
|
|
|
|
500 |
68 |
68 |
96 |
110 |
|
|
|
|
|
|
600 |
76 |
76 |
104 |
|
|
|
|
|
|
|
700 |
82 |
82 |
|
|
|
|
|
|
|
Красным цветом обозначен максимальный суммарный эффект от выделения соответствующего размера инвестиций 4 предприятиям.
|
ξ |
0 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
|
F4(ξ) |
0 |
28 |
50 |
65 |
79 |
91 |
105 |
117 |
|
z4 |
0 |
0 |
1 |
2 |
2 |
2 |
2 |
3 |
Сведем результаты в 4 таблицы. Теперь F4(700)=117 показывает максимальный суммарный эффект по всем 4-м фирмам, аz4(700)=300 – размер инвестиций в 4-ю фирму для достижения этого максимального эффекта. После этого на долю первых 3-х фирм осталось (700-300) и для достижения максимального суммарного эффекта по первым 3-м фирмам в 3-ю надо вложить200 и т.д. Красным отмечены оптимальные значения инвестиций по фирмам (zi) и значения эффектов от них (Fi(ξ)).
|
ξ |
0 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
|
|
|
|
|
|
|
|
|
|
|
F1(ξ) |
0 |
28 |
42 |
51 |
57 |
61 |
64 |
66 |
|
z1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
F2(ξ) |
0 |
28 |
42 |
51 |
62 |
71 |
80 |
87 |
|
z2 |
0 |
0 |
0 |
0 |
2 |
2 |
3 |
4 |
|
F3(ξ) |
0 |
28 |
42 |
54 |
68 |
79 |
89 |
99 |
|
z3 |
0 |
0 |
0 |
2 |
2 |
3 |
4 |
3 |
|
F4(ξ) |
0 |
28 |
50 |
65 |
79 |
91 |
105 |
117 |
|
z4 |
0 |
0 |
1 |
2 |
2 |
2 |
2 |
3 |