8. Задача формирования оптимального портфеля ценных бумаг
Перед
нами стоит задача сформировать оптимальный
портфель заданной эффективности из
трёх видов ценных бумаг: безрисковых
эффективности 2 и некоррелированных
рисковых ожидаемой эффективности 4 и 9
и рисками 8 и 12. Определить, как устроена
рисковая часть оптимального портфеля,
а также при какой ожидаемой эффективности
портфеля возникает необходимость в
операции “short
sale”
и с какими ценными бумагами.
При
исследовании финансового рынка дисперсию
иногда называют вариацией V
и рискованность обычно отождествляют
со средним квадратическим отклонением.
Итак,
получили m0
= 2;
 ;
;
 .
.
Зададимся
эффективностью портфеля mp.
Находим
обратную матрицу к матрице V,
она равна

Теперь вычисляем
знаменатель:

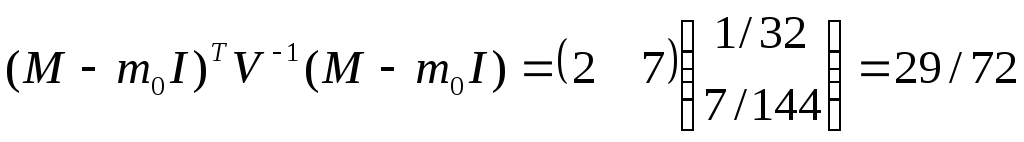
Оптимальное значение
долей есть
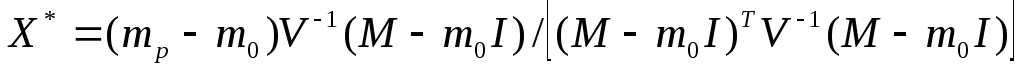
Подставив полученные
ранее значения, получим
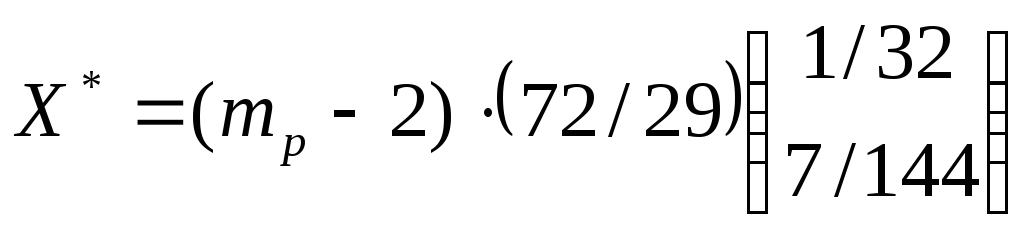
Отсюда рисковые
доли соответственно равны:
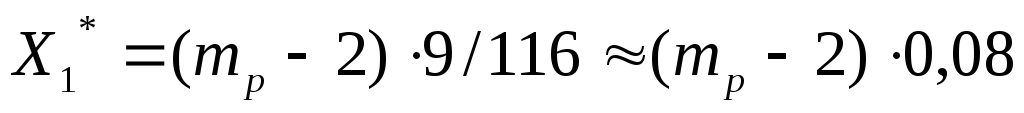

Следовательно,
безрисковая доля:

Найдём
теперь значение mp,
при котором возникает необходимость в
проведении операции “short
sale”:

При mp
> 7, то X0*
< 0 и необходимо
провести операцию “short sale”
Использованная литература:
Методические указания
к выполнению курсовой работы по дисциплине
“Прикладная математика” / Сост.: Колемаев
В.А., Карандаев И.С., В.И. Малыхин, Т.М.
Гатауллин, Ю.Г. Прохоров, Х.Х. Юнисов;
ГУУ, М., 2000. 73 с.
-
22-


