В. Принятие решений в условиях частичной неопределенности.

Предположим, что в рассматриваемой схеме известны вероятности того, что реальная ситуация развивается по варианту.Именно такое положение называется частичной неопределенностью. Как здесь принимать решение? Можно выбрать одно из следующих правил.

Правило максимизации среднего ожидаемого дохода. Доход, получаемый фирмой при реализации -горешения, является случайной величиной с рядом распределения

		…
		…

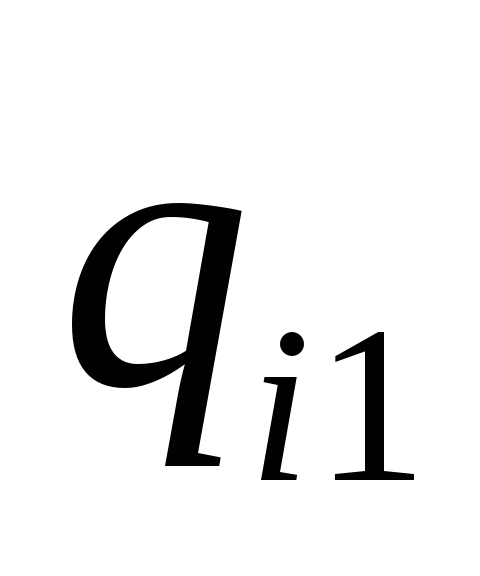
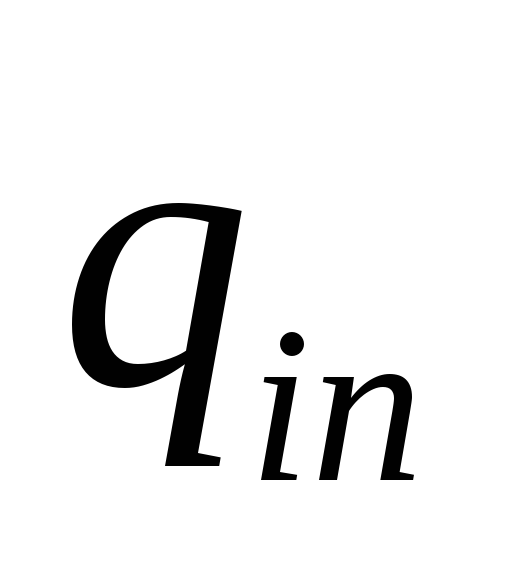
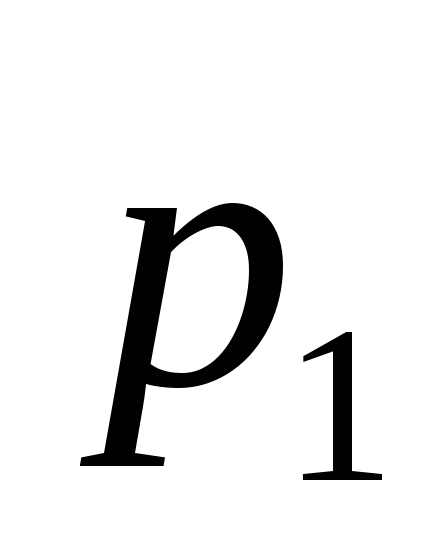
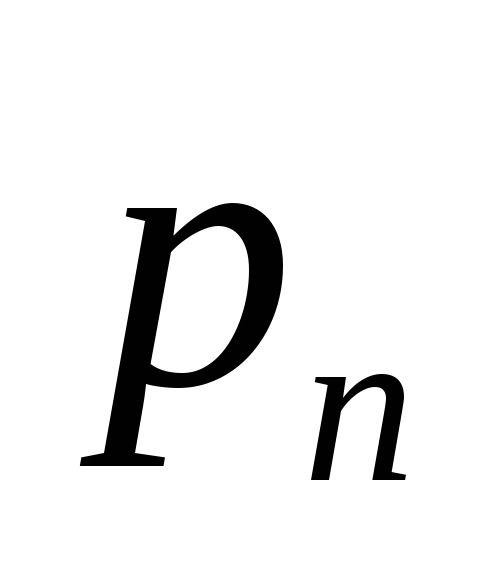
Математическое ожидание и есть средний ожидаемый доход, обозначаемый также .Итак, правило рекомендует принять решение, приносящее максимальный средний ожидаемый доход.

Предположим, что в схеме из предыдущего п. вероятности есть (1/20, 1/4, 1/5, 1/2).Тогда

Максимальный средний ожидаемый доход равен 18,6 –соответствует 2-у решению.

Правило минимизации среднего ожидаемого риска. Риск фирмы при реализации -горешения, является случайной величинойс рядом распределения

		…
		…

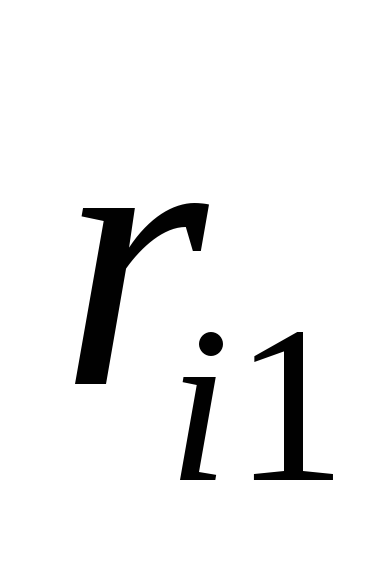
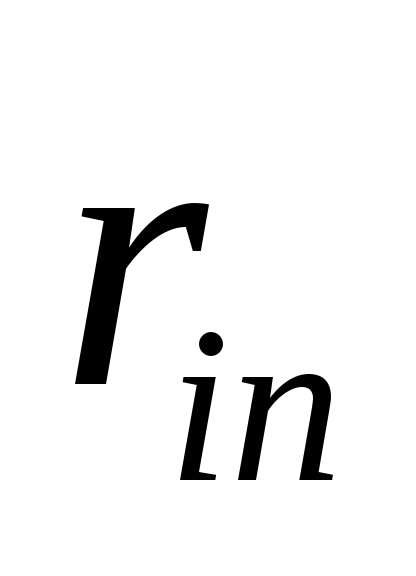
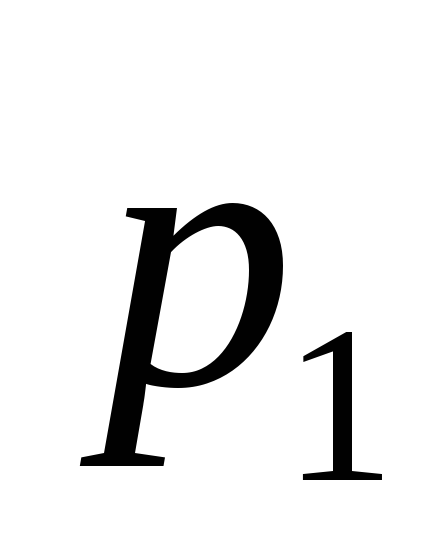
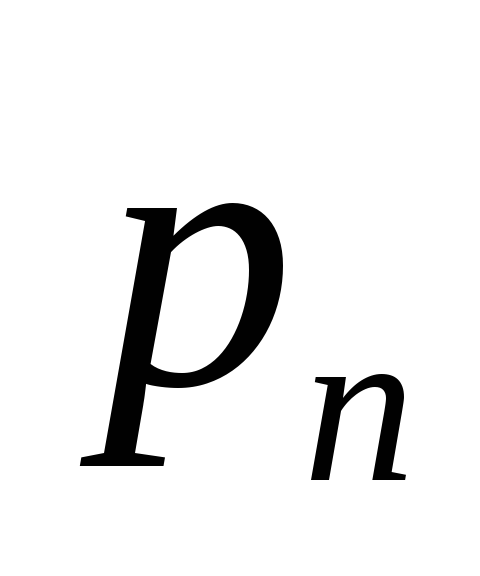
Математическое ожидание и есть средний ожидаемый риск, обозначаемый также .Правило рекомендует принять решение, влекущее минимальный средний ожидаемый риск.

Вычислим средние ожидаемые риски при указанных выше вероятностях. Получаем Минимальный средний ожидаемый риск равен1,9,соответствует 2-у решению.

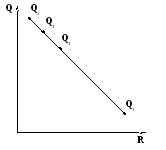Нанесем средние ожидаемые доходы и средние ожидаемые риски на плоскость – доход откладываем по вертикали, а риски по горизонтали (см. рис.):

Получили 4точки. Чем выше точка , тем более доходная операция, чем точка правее –тем более она рисковая. Значит, нужно выбирать точку выше и левее. Точка доминирует точку , еслии и хотя бы одно из этих неравенств строгое. В нашем случае 2-я операция доминирует все остальные.

Точка, не доминируемая никакой другой называется оптимальной по Парето, а множество всех таких точек называется множеством оптимальности по Парето. Легко видеть, что если из рассмотренных операций надо выбрать лучшую, то ее обязательно надо выбрать из операций, оптимальных по Парето. В нашем случае, множество Парето, т.е. оптимальных по Парето операций, состоит только из одной 2-й операции.

Для уточнения распределения вероятностей можно провести пробную операцию. После ее проведения вероятности состояний, характеристики операций и оптимальные решения могут стать совершенно иными.

Первоначальные вероятности и средний ожидаемый доход:

2	6	8	22	14,2
0	4	8	32	18,6
-6	-4	0	10	3,7
0	8	12	24	16,4
1/20	1/4	1/5	1/2

Первоначальные вероятности и средний ожидаемый риск:

0	2	4	10	6,3
2	4	4	0	1,9
8	12	12	22	16,8
2	0	0	8	4,1
1/20	1/4	1/5	1/2

Вероятности и средний ожидаемый доход после пробной операции:

2	6	8	22	20,0
0	4	8	32	28,8
-6	-4	0	10	8,4
0	8	12	24	21,6
0,1	0	0	0,9

Вероятности и средний ожидаемый риск после пробной операции:

0	2	4	10	9,0
2	4	4	0	0,2
8	12	12	22	20,6
2	0	0	8	7,4
0,1	0	0	0,9

Максимально оправданная стоимость пробной операции – 10,2.

Для нахождения лучшей операции иногда применяют подходящую взвешивающую формулу, которая для пар дает одно число, по которому и определяют лучшую операцию. Например, пусть взвешивающая формула есть. Тогда получаем:. Видно, что 2-я операция – лучшая, а 3-я – худшая.

Правило Лапласа. Иногда в условиях полной неопределенности применяют правило Лапласа равновозможности, когда все вероятности считают равными. После этого можно выбрать какое-нибудь из двух приведенных выше правил-рекомендаций принятия решений.