3.3. Матричная игра как модель конкуренции и сотрудничества

Пусть игроки – Первый и Второй, играют в матричную игру с матрицей . Пусть стратегия Первого есть, а Второго –. Тогда выигрыш Первого есть случайная величина (с.в.)с рядом распределения:

			…				…
			…				…

Математическое ожидание этой с.в., т.е. есть средний выигрыш Первого. Пустьесть дисперсия этой с.в. Естественно назвать среднее квадратическое отклонение с.в., т.е.риском для Первого при игре со стратегиями. Поскольку выигрыш Первого есть проигрыш для Второго, тоесть случайный проигрыш Второго ивполне естественно можно назвать риском игры с такими стратегиями и для Второго.

Предположим сначала, что игроки озабочены только максимизацией среднего дохода за партию игры – обычная цель в таких играх. Тогда игроки будут играть со своими оптимальными стратегиями: – Первый игрок и– Второй.

Математическое ожидание с. в. называется ценой игры, обозначим ее.

Но что же назвать риском всей игры?

Вычислим дисперсию выигрыша Первого при оптимальных стратегиях игроков.

.

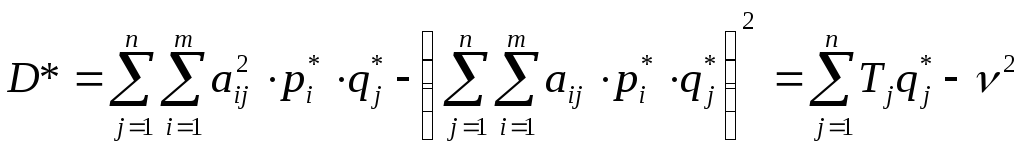Так как , а черезсумма обозначена.

Заметим, что в сумме можно оставить лишь те слагаемые, у которых

Заметим теперь, что если Первый играет со стратегией , а Второй отвечает-й чистой стратегией, то выигрыш первого есть с.в. с рядом распределения:

			…				…
			…				…

Если есть оптимальная стратегия Первого, а, то из теории матричных игр с нулевой суммой известно, что выигрыш Первого при таких стратегиях по-прежнему равен цене игры, а дисперсия выигрыша Первого при этом равна, то есть равна. Таким образом, что происходит с риском выигрыша Первого, можно понять, сравнив дисперсию при оптимальных стратегияхи дисперсиюили величиныи. ПустьКак легко понять, если средиесть разные числа, то

Теперь можно сделать следующий вывод:

Чуть-чуть отойдя от своей оптимальной стратегии (смотрите ниже Пример) и таким образом почти не уменьшив свой выигрыш, Первый может значительно уменьшить свой риск. При этом уменьшается и риск Второго, что отвечает и его интересам.

Чисто математически можно сказать, что в описанной ситуации риск выигрыша Первого не зависит от его стратегии непрерывно.

Рассмотрим подробно пример матричной игры с матрицей . Как известно, общий случай в окрестности оптимальных стратегий игроков сводится к анализу такой игры.

Пример. Пусть матрица игры есть. Графическое решение этой игры показано на рисунке.

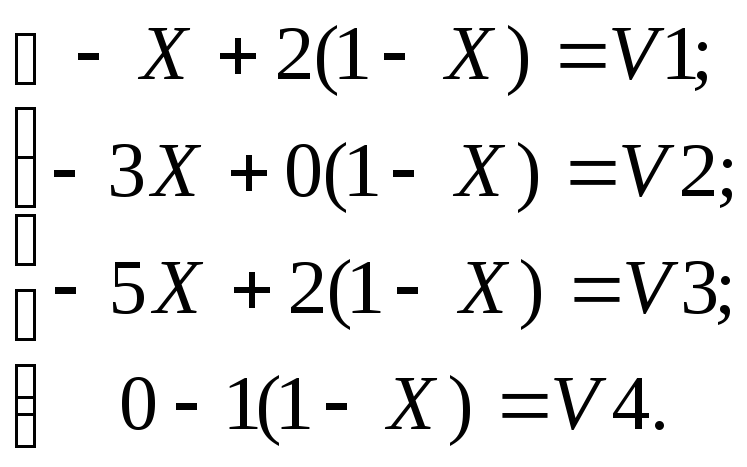
На рисунке ищем верхнюю точку нижней огибающей. Эта точка показывает цену игры и оптимальную стратегию первого игрока.

Так как прямые V1 иV3 находятся выше точкиO, то вероятности 1-й и 3-й стратегий равны 0.

Оптимальные стратегии: ????????????????
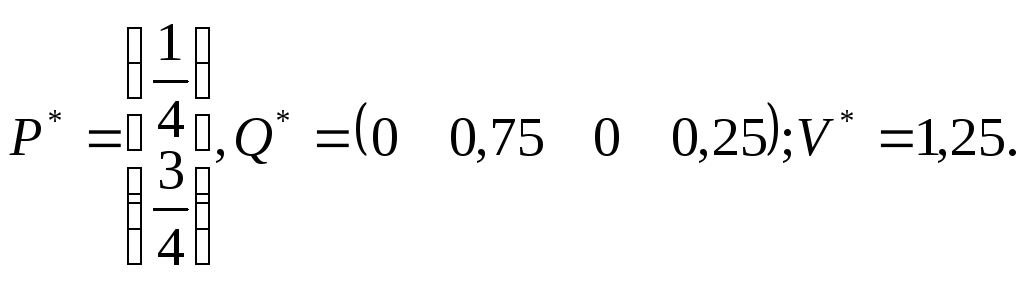