2.4.Статистический анализ денежных потоков.

Анализ суточных вкладов в отделение Сбербанка.

Исходные данные для анализа: ежедневные (суммарные) денежные вклады населения в отделение сбербанка в течение 4- недель (или аналогичный какой-нибудь денежный поток). Для удобства обработки все числа предполагаются целыми двузначными, что всегда можно сделать округлением и масштабированием.

Вариант данных:

1-я неделя	2-я неделя	3-я неделя	4-я неделя
1 2 3 4 5 6	1 2 3 4 5 6	1 2 3 4 5 6	1 2 3 4 5 6
	Денежный поток
15 14 13 9 9 9	9 9 9 12 12 12	12 12 12 2 0 16	18 5 4 6 5 13

Статистические характеристики I:

Ранжированный ряд:

0 2 4 5 5 6 9 9 9 9 9 9 12 12 12 12 12 12 13 13 14 15 16 18

Дискретный вариационный ряд:

0	2	4	5	6	9	12	13	14	15	16	18
1	1	1	2	1	6	6	2	1	1	1	1
1/24	1/24	1/24	2/24	1/24	6/24	6/24	2/24	1/24	1/24	1/24	1/24

p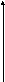_i

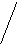
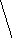
6/24

0 2 4 5 6 9 12 13 14 15 16 18 x_i

Статистические характеристики II:

Интервальный вариационный ряд:

Интервалы	0-2	2-4	4-6	6-8	8-10	10-12	12-14	14-16	16-18	18-20
Центральное значение интервала	1	3	5	7	9	11	13	15	17	CAPut!’
Частоты	1/24	1/24	3/24	1/24	6/24	0/24	8/24	2/24	1/24	1/24

Многоугольник частостей:

График выборочной функции распределения:

F

1

1 3 5 7 9 11 13151719 хX

f

8/48

1/48

1 3 5 7 9 1113 151719 х

1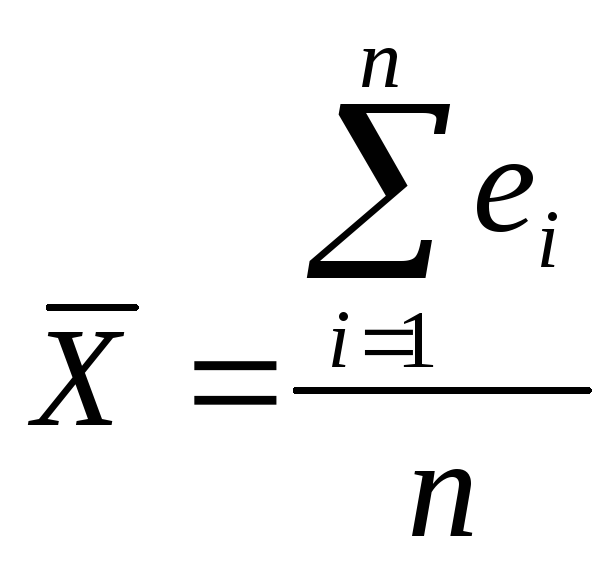.По исходным данным:

, где е_i- размер вклада, n- объем выборки

В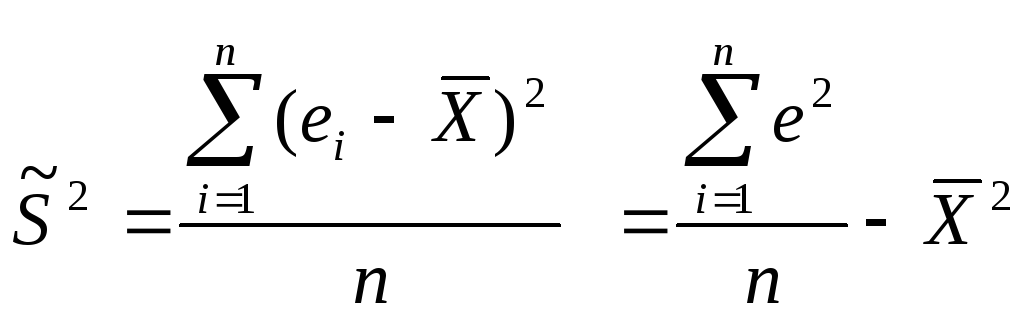ыборочная дисперсия:

Выборочное СКО:

Несмещенная оценка генеральной дисперсии:

2. По дискретному вариационному ряду:

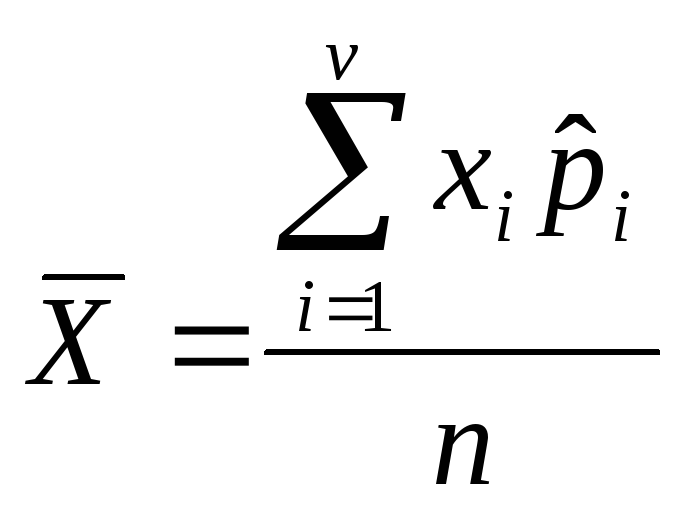,где p_i - частость, v- число вариантов выборки,

х_i- одинаковые как числа элементы

В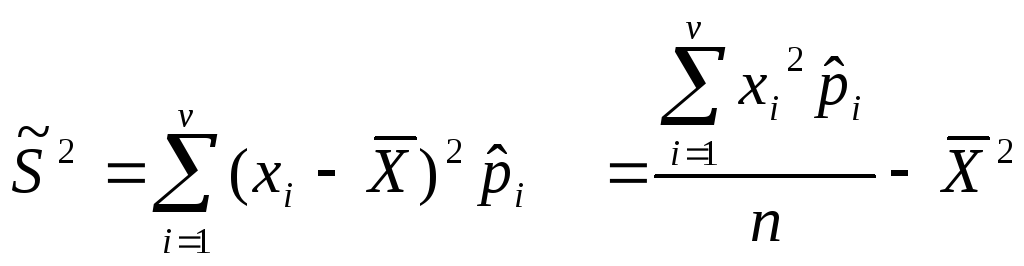ыборочная дисперсия:

Выборочное СКО:

Несмещенная оценка генеральной дисперсии:

3. По интервальному вариационному ряду:

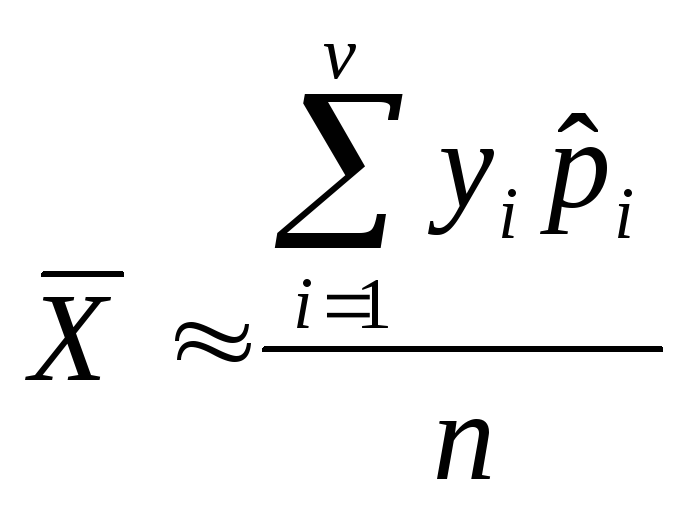
Выборочная дисперсия:

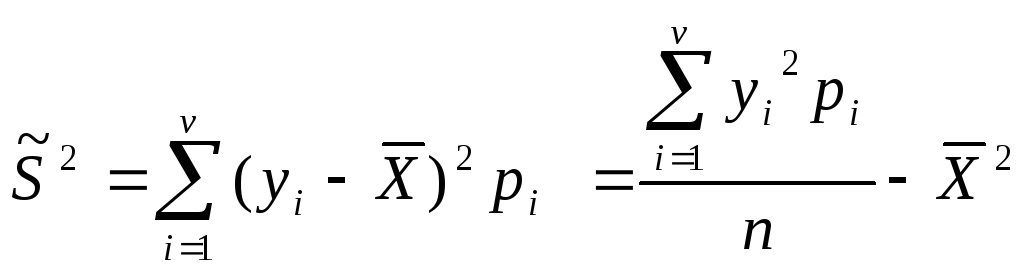
Выборочное СКО:

Несмещенная оценка генеральной дисперсии:

Несмещенной оценкой генеральной средней (математического ожидания) служит выборочная средняя:

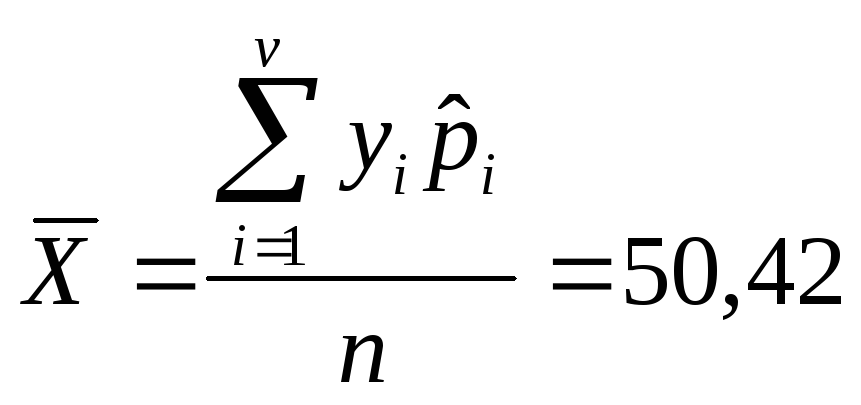
Несмещенная оценка генеральной дисперсии:

Понятие генеральной совокупности в терминах денежного потока означает все когда-либо осуществляемые вклады населения в отделение сбербанка. Понятие генеральной средней означает средний вклада среди всех когда-либо осуществлявшихся в отделение сбербанка.

5) Интервальный вариационный ряд: границы интервала [0;20], шаг h=2, число интервалов v=10.

H=2	[0,2)	[2,4)	[4,6)	[6,8)	[8, 10)	[10,12)	[12,14)	[14,16)	[16,18)	[18,20)
	1	3	5	7	9	11	13	15	17	CAPut!’
pi	1/24	1/24	3/24	1/24	6/24	0/24	8/24	2/24	1/24	1/24

График выборочной функции плотности:

f

8/48

1/48

1 3 5 7 9 11 13 15 17 19 х