
- •Государственный университет управления
- •1.1 Линейная производственная задача.
- •1.2 Двойственная задача линейного программирования.
- •1.3. Задача о «расшивке узких мест».
- •1.4.Задача о комплектном плане.
- •1.5 Оптимальное распределения ресурсов.
- •2.1. Принятие решения в условиях неопределенности.
- •2.2. Анализ доходности и рискованности финансовой операции.
- •2.3. Задача формирования оптимального портфеля ценных бумаг.
- •2.4 Статистический анализ денежных потоков.
- •§3. Модели сотрудничества и конкуренции.
- •3.1. Сотрудничество и конкуренция двух фирм на рынке одного товара. Независимое поведение двух фирм
- •Стратегия Курно
- •Стратегия Стакельберга.
- •Объединение двух фирм.
- •3.2. Кооперативная биматричная игра как модель сотрудничества и конкуренции двух участников.
- •3.3 Матричная игра как модель конкуренции и сотрудничества.
- •§.4. Социально-экономическая структура общества
- •4.1. Модель распределение богатства в обществе
- •4.2.Распределение общества по получаемому доходу
- •Литература:
1.3. Задача о «расшивке узких мест».
|
СБ |
Б |
Н |
36 |
30 |
16 |
12 |
0 |
0 |
0 |
|
|
Х1 |
Х2 |
Х3 |
Х4 |
Х5 |
Х6 |
Х7 | ||||
|
30 |
Х2 |
16 |
0 |
1 |
-2/15 |
7/15 |
1/5 |
-2/15 |
0 |
|
|
36 |
Х1 |
25 |
1 |
0 |
2/3 |
1/6 |
0 |
1/6 |
0 |
|
|
0 |
Х7 |
28 |
0 |
0 |
104/15 |
26/15 |
-7/5 |
14/15 |
1 |
|
|
|
Р |
1380 |
0 |
0 |
4 |
8 |
6 |
2 |
0 |
|
При выполнении оптимальной производственной программы первый и второй ресурсы используются полностью, тем самым они образуют "узкие места" производства. Будем их заказывать дополнительно. Пусть T = (t1,t2, 0) — вектор дополнительных объемов ресурсов. Так как мы будем использовать найденные двойственные оценки ресурсов, то должно выполняться условие H + Q–1 = 0 или H– Q–1T, где H — значения базисных переменных в последней симплексной таблице, а Q–1 — обращенный базис, который образуют столбцы при балансовых переменных в этой таблице. Задача состоит в том, чтобы найти вектор T , максимизирующий суммарный прирост прибыли W = 6t1 + 2t2 (1) при условии, сохранения двойственных оценок ресурсов (и, следовательно ассортимента выпускаемой продукции),








 (2)
(2)
предполагая, что можно получить дополнительно не более 1/3 первоначального объема ресурсов каждого вида.




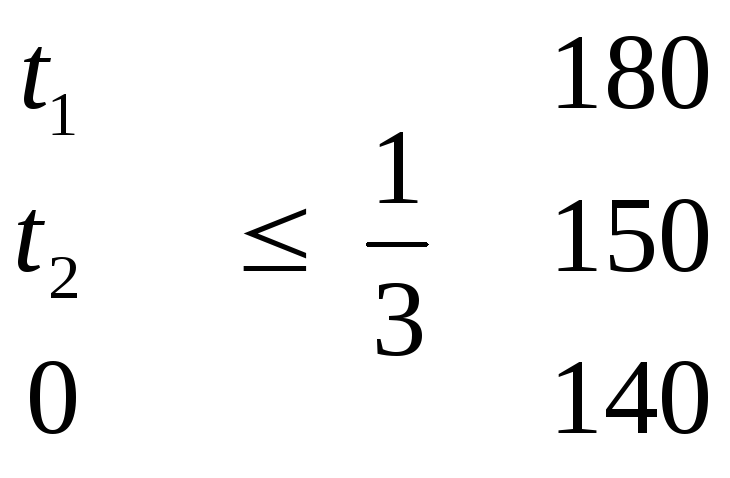 (3)
(3)
причем по смыслу задачи t1 ≥ 0, t3 ≥ 0 (4)
Переписав неравенства (2) и (3) в виде:
—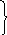 1/5t1
+ 2/15t2
≤ 16
1/5t1
+ 2/15t2
≤ 16
0t1 — 1/6t2 ≤ 25 (5)
7/5t1 — 14/15t2 ≤ 28
![]() (6)
(6)
приходим к задаче ЯП; максимизировать (1) при условиях (5), (6) и (4).
Э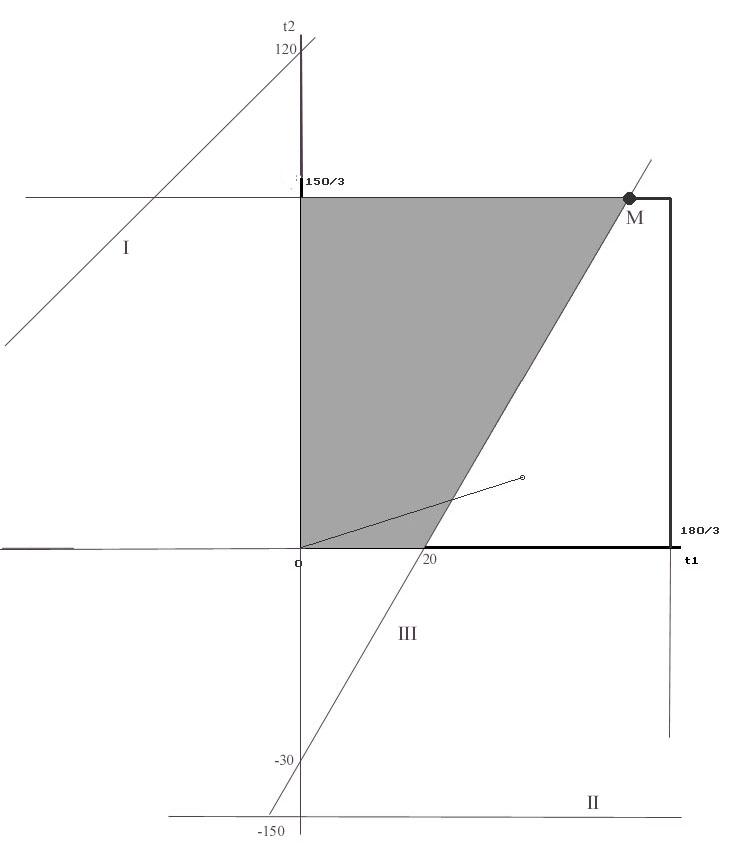 ту
задачу легко решить графически: см.
рис.. Программа "расшивки" имеет
видt1= 531/3
, t2= 50,t3=
0, а прирост прибыли составил maxW = 420.
ту
задачу легко решить графически: см.
рис.. Программа "расшивки" имеет
видt1= 531/3
, t2= 50,t3=
0, а прирост прибыли составил maxW = 420.
Сводка результатов приведена в таблице 1.
Таблица 1.
|
ci |
36 |
30 |
16 |
12 |
b |
x4+i |
yi |
ti |
|
aij |
4 |
5 |
2 |
3 |
180 |
0 |
6 |
53 1/3 |
|
6 |
0 |
4 |
1 |
150 |
0 |
2 |
50 | |
|
0 |
7 |
6 |
5 |
140 |
28 |
0 |
0 | |
|
xj |
25 |
16 |
0 |
0 |
1380 |
|
|
420 |
|
Δj |
0 |
0 |
4 |
8 |
|
|
|
|
1.4.Задача о комплектном плане.
Предположим, что в линейной производственной задаче продукция производится комплектно: 4-го вида продукции необходимо произвести в 5 раза больше, чем 2-го, а 1-го столько в 2 раза больше чем 3-го. Таким образом, имеем: х3 = 2х1, х4 = 5х2. Подставим эти выражения в задачу из пункта 1.1 и получим задачу ЛП с двумя переменными:
-
Исходная задача ЛП:
Задача ЛП с двумя переменными:
P(x1, x2, x3, x4) = 36x1 + 30х2 + 16x3 + 12x4 max (4)
4x1 + 5х2 + 2x3 + 3x4 180
6x1 + 0х2 + 4x3 + x4 150 (5)
0x1 + 7х2 + 6x3 + 5x4 140
x1 — 4 0
Р = 68х1+90х2 max,
8x1 + 20х2 180 (1)
14x1 + 5х2 150 (2)
12x1 + 32х2 140 (3)
x1,x2 0
Б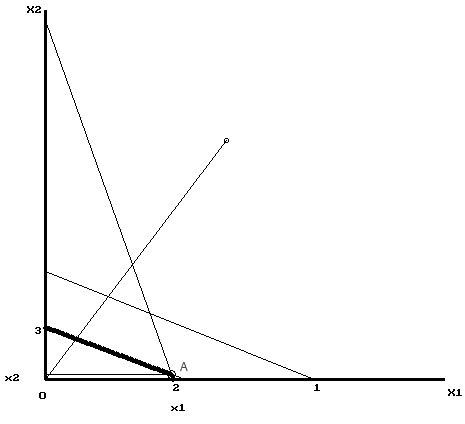 удем
решать задачу графически: исходя из
ограничений, построим допустимое
множество задачи (пересечение 3-х
полуплоскостей, выпуклый многоугольник),
затем построим линию уровня целевой
функции и будем двигать ее параллельно,
стараясь уловить последнюю точку
пересечения линии с допустимым множеством.
удем
решать задачу графически: исходя из
ограничений, построим допустимое
множество задачи (пересечение 3-х
полуплоскостей, выпуклый многоугольник),
затем построим линию уровня целевой
функции и будем двигать ее параллельно,
стараясь уловить последнюю точку
пересечения линии с допустимым множеством.
Искомая точка А находится как решение системы:
![]()
 14x1
+ 5х2
= 150
14x1
+ 5х2
= 150
12x1 + 32х2 = 140 х1=10,57, х2=0,41
Максимальное значение целевой функции примерно равно 755,67.
