Но что же назвать риском всей игры?

Вычислим дисперсию выигрыша Первого при оптимальных стратегиях игроков.

.

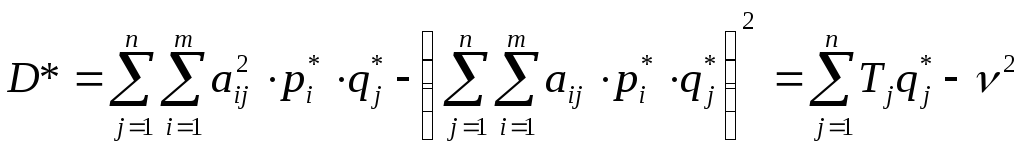Так как , а черезсумма обозначена.

Заметим, что в сумме можно оставить лишь те слагаемые, у которых

Заметим теперь, что если Первый играет со стратегией , а Второй отвечает-й чистой стратегией, то выигрыш первого есть с.в. с рядом распределения:

			…				…
			…				…

Если есть оптимальная стратегия Первого, а, то из теории матричных игр с нулевой суммой известно, что выигрыш Первого при таких стратегиях по-прежнему равен цене игры, а дисперсия выигрыша Первого при этом равна, то есть равна. Таким образом, что происходит с риском выигрыша Первого, можно понять, сравнив дисперсию при оптимальных стратегияхи дисперсиюили величиныи. ПустьКак легко понять, если средиесть разные числа, то

Теперь можно сделать следующий вывод:

Чуть-чуть отойдя от своей оптимальной стратегии (смотрите ниже Пример) и таким образом почти не уменьшив свой выигрыш, Первый может значительно уменьшить свой риск. При этом уменьшается и риск Второго, что отвечает и его интересам.

Рассмотрим подробно пример матричной игры с матрицей . Как известно, общий случай в окрестности оптимальных стратегий игроков сводится к анализу такой игры.

П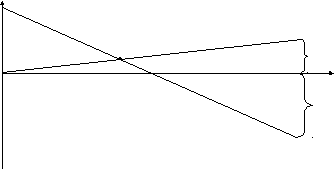ример. Пусть матрица игры есть. Графическое решение этой игры показано на рисунке 1.

2

1

1

2

Рис.1

Цена игры , оптимальные стратегии игроков есть,. Дисперсия выигрыша Первого при оптимальных стратегиях, т. е. риск игры равен примерно 1. Далее вычисления дают,;,Примерная, но достаточно точная зависимость риска Первого в малой окрестности его оптимальной стратегии показана на рис. 2.

1

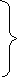
1

Рис.2 2/5

Как видно из рис. 2 при отходе Первого от своей оптимальной стратегии вправо, т. е. при увеличении вероятности выбора им 1-й строки. Второй начинает отвечать 1-й чистой стратегией и риск Первого скачком увеличивается до, а при отходе Первого от своей оптимальной стратегии влево Второй переходит на свою 2-ю чистую стратегию и риск Первого скачком снижается до

1

Рис.3 1/5

Аналогичное верно и в отношении Второго. Кратко повторим. Примерная, но достаточно точная зависимость риска Второго в малой окрестности его оптимальной стратегии показана на рис. 3. Как видно из рис. 3 при отходе второго от своей оптимальной стратегии вправо, т. е. при увеличении вероятности выбора им 1-й строки Первый начинает отвечать 2-й чистой стратегией и риск Второго скачком уменьшается до, а при отходе второго от своей оптимальной стратегии влево Первый переходит на свою 1-ю чистую стратегию и риск Второго скачком увеличивается до

Пусть . Эту величину и можно назвать риском всей игры. Однако играть с таким риском можно лишь при согласии обеих сторон. Для анализируемой игрыи игроки для достижения такого риска должны играть так: Первый играет со своей оптимальной стратегией3,5), а Второй должен использовать 2-ю чистую стратегию.

§.4. СОЦИАЛЬНО-ЭКОНОМИЧЕСКАЯ СТРУКТУРА ОБЩЕСТВА

1. Модель распределения богатства в обществе.

Такой моделью является так называемая “диаграмма или кривая Лоренца распределения богатства в обществе.

Рассмотрим функцию , которая сообщает, что-я часть самых бедных людей общества владеет-й частью всего общественного богатства (см. рис.). Если бы распределение богатства было бы равномерным, то график функциишел бы по диагонали квадрата.

Поэтому, чем меньше площадь заштрихованной линзы, тем равномернее распределено богатство в обществе. Величина этой площади называется также коэффициентом Джинни.

Исходя из содержательного смысла функции можно доказать, что эта функция и первые ее две производные положительны на [0,1].

Пример 1. Пусть . Тогда ,т. е. пятая часть самых бедных владеет только всего богатства и т. д. Вычислим коэффициент Джинни. Имеем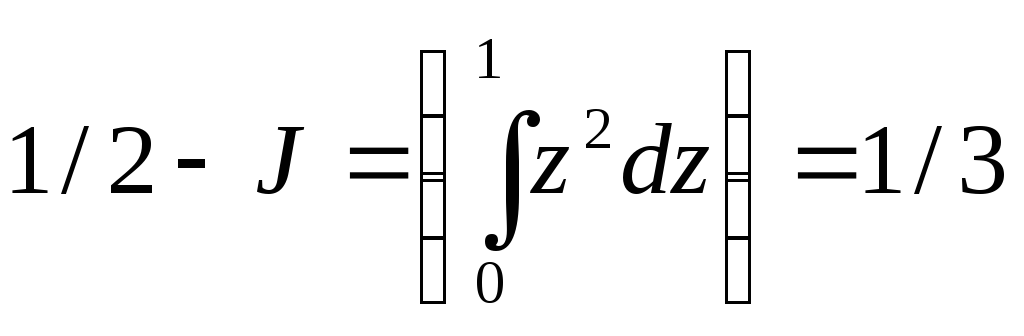, значит,.

Назовем распределение богатства в обществе опасно несправедливым, если . Следовательно, функцияне свидетельствует об опасно несправедливом распределении богатства.

Зная функцию найдем другую функцию«такую часть всего богатства общества имеет-я часть самых богатых людей». Имеем..В частности, для функции из примера получаем. Так что, в этом случае, десятая часть самых богатых владеет 19% всего богатства или примерно пятой частью.

По функции определим еще одну функцию:Эта функция определена на отрезке [0,1/2]. О смысле этой функции догадайтесь сами.

Как найти часть богатства, которой владеет срединная часть общества – богаче, чем 1/4 самых бедных, но беднее, чем 1/4 самых богатых?

Эта часть равна

Скажем, что в обществе есть средний класс, если эта часть не менее 1/2. Есть ли средний класс при функции распределения богатства ? Для ответа вычисляем . Окончательный ответ: есть.

Отметим, что функции ,,не дают представления об абсолютном богатстве общества, а лишь о распределении богатства внутри него.

2. Распределение общества по получаемому доходу.

Пусть есть доля получающих месячный доход меньшепо отношению ко всем, имеющим какой-нибудь денежный доход (всех таких членов общества назовем налогоплательщиками). Функциювполне правильно трактовать, как функцию распределения случайной величины (с. в.)-месячный доход случайного налогоплательщика. С. в.можно считать непрерывной. Функцияможет быть интересна для налоговой инспекции.

Пример 2. Конкретно, пусть =1-(2000/2000+).

Определим размер месячного дохода, который для случайно выбранного налогоплательщика может быть превзойден с вероятностью 0,5. Найдем также средний месячный доход.

1

Решение. Удобно решить эту задачу в общем виде – для функции ,,и произвольной вероятности. График функции см. на рис.

Итак найдем размер месячного дохода B, который для случайно выбранного налогоплательщика может быть превзойден с вероятностью p. Так какесть вероятность, то. Следовательно,и окончательно,. Для рассматриваемого примера получаем

Теперь найдем средний месячный доход. Сначала найдем плотность распределения с. в.. Она есть производная функции. Таким образом,.

Средний месячный доход есть математическое ожидание с. в. I, т. е., и дальнейшие вычисления даютДля рассматриваемого примера получаем.

Важным показателем является коэффициент Рейнбоу. Он находится так: найдем решение уравнения , обозначим его, затем найдем решение уравнения, обозначим его, тогда коэффициент Ренйбоу есть.

Отметим, что в отличие от функций ,,из пункта 4.1., которые не дают представления об абсолютном богатстве общества, а лишь о распределении богатства внутри него, функция, как раз наоборот, дает довольно хорошее представление об уровне жизни.