2. Двойственная задача

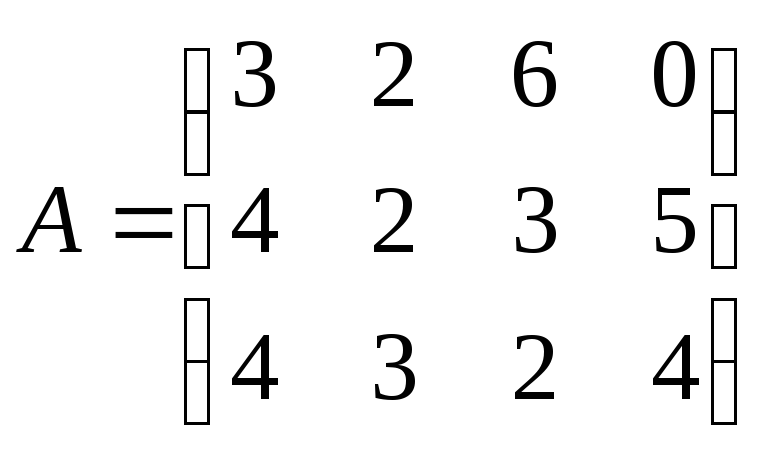
Некое предприятие «КПО», использующее те же ресурсы что и предприятие из предыдущей задачи, желает приобрести все эти ресурсы. Оно желает приобрести их по ценам y₁, y₂ и y₃ соответственно за единицу каждого из трёх ресурсов. Величины у₁, у₂, у₃ принято называть расчетными, или двойственными, оценками ресурсов. Из условий предыдущей задачи нам известны затраты всех 3-х ресурсов для производства для каждого из 4-х видов продукции (A), количество ресурсов на производстве (B) и прибыль от единицы каждой продукции (C):

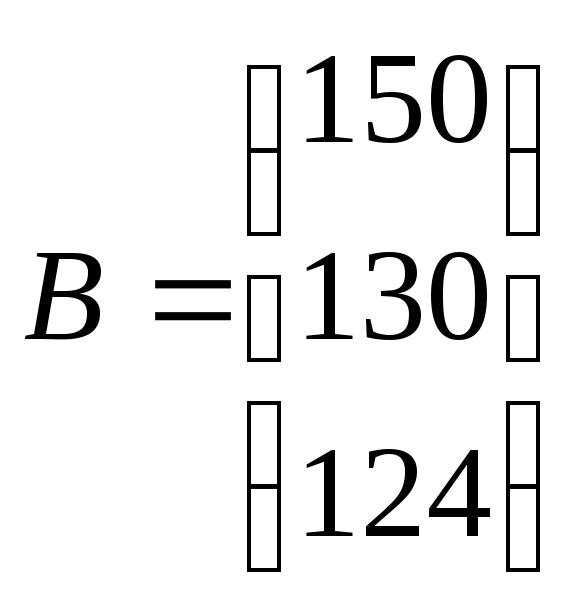
Для производства единицы продукции первого вида мы должны затратить, как видно из матрицы А, 3 единицы ресурса первого вида, 4 единицы ресурса второго вида и 4 единицы третьего. В ценах у₁, у₂, у₃ наши затраты составят 3у₁ + 4у₂ + 4у₃, т.е. столько заплатит предприятие «КПО» за все ресурсы, идущие на производство единицы первой продукции. На рынке за единицу первой продукции мы получили бы прибыль 30. Следовательно, мы можем согласиться с предложением предприятия «КПО» только в том случае, если он заплатит не меньше 30 :

3у₁ + 4у₂ + 4у₃  30.

Соответственные условия должны выполняться и для продукции других видов, т.е.

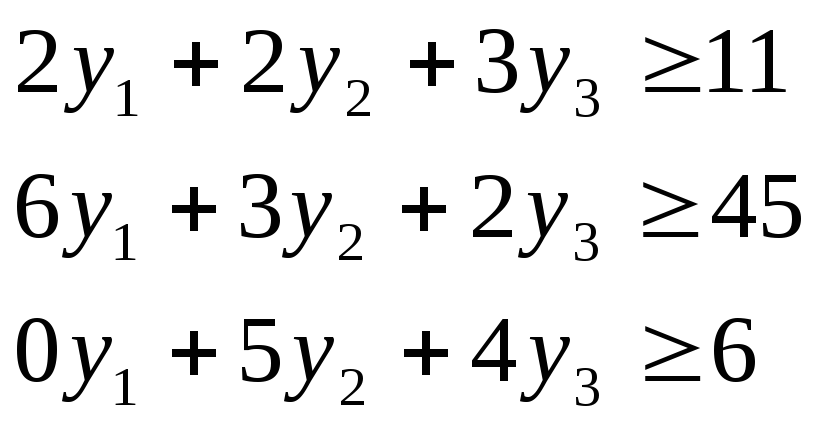
Но при продаже требуется учитывать и интересы покупателя. Естественным желанием покупателя является снижение расходов. Так как предприятие желает закупить весь объём имеющихся ресурсов, то его затраты при ценах y₁, y₂ и y₃ составят , где коэффициенты приy₁, y₂ и y₃ - количество имеющихся ресурсов. Таким образом:

→min

Кроме того, так как цены не могут быть отрицательными, то .

Решение полученной задачи легко найти с помощью второй основной теоремы двойственности, согласно которой для оптимальных решений х(х₁,х₂,х₃,x₄) и у(у₁,у₂,у₃) пары двойственных задач необходимо и достаточно выполнение условий:

x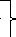₁ (3y₁ + 4y₂ + 4y₃ - 30) = 0 y₁ (3x₁ + 2x₂ + 6x₃ - 150) = 0

x ₂ (2y₁ + 2y₂ + 3y₃ - 11) = 0 y₂ (4x₁ + 2x₂ + 3x₃ + 5x₄ - 130) = 0

x ₃ (6y₁ + 3y₂ + 2y₃ - 45) = 0 y₃ (4x₁ + 3x₂ + 2x₃ + 4x₄ - 124) = 0 .

x ₄ ( + 5y₂ + 4y₃ - 6) = 0

Ранее (см. Задачу 1) было найдено, что в решении исходной задачи х₁>0 и х₃>0. Поэтому

3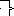y₁ + 4y₂ + 4y₃ - 30 = 0

6y₁ + 3y₂ + 2y₃ - 45 = 0

Учитывая, что 3-ой ресурс был избыточным, то, согласно теореме двойственности, его двойственная оценка , получим систему:

3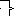y₁ + 4y₂ - 30 = 0

6y₁ + 3y₂ - 45 = 0 откуда следует у₁ = 6, у₂ = 3.

Таким образом, получили двойственные оценки ресурсов: у₁ = 6, у₂ = 3, у₃ = 0

причем общая оценка всех ресурсов равна 150*6+130*3+124*0=1290

Решение содержится в последней строке последней симплексной таблицы исходной задачи.

Экономический смысл двойственных оценок:

• двойственная оценка первого ресурса у₁=6 показывает, что добавление одной единицы первого ресурса обеспечит прирост максимальной прибыли в 6 единиц;

• двойственная оценка второго ресурса у₂=3 показывает, что добавление одной единицы второго ресурса обеспечит прирост прибыли в 3 единицы;

• оценка второй технологии Δ₂ = 7 показывает, что если произвести одну единицу продукции второго вида (она не входит в оптимальную производственную программу), то прибыль уменьшится на 7 единиц;

• оценка четвертой технологии Δ₄ = 9 показывает, что если произвести одну единицу продукции четвертого вида (она не входит в оптимальную производственную программу), то прибыль уменьшится на 9 единиц.