- Область устойчивости двойственных оценок, где

- вектор свободных членов системы ограничений из 1-ой задачи

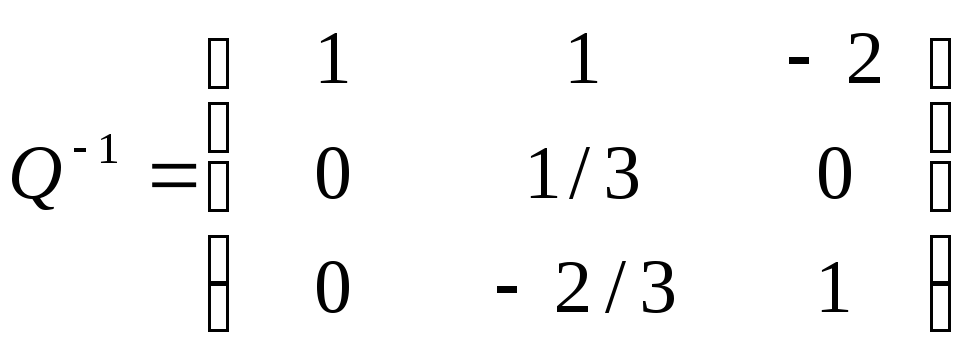- обращённый базис

- вектор дополнительных объемов ресурсов

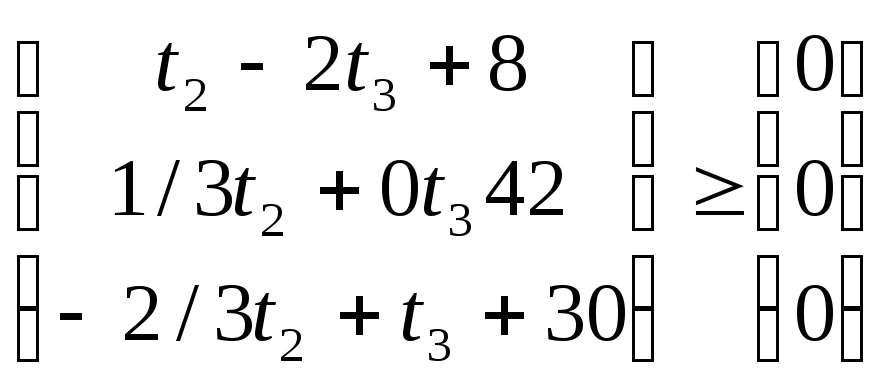
Кроме того, закупки ресурсов не могут превышать трети ресурсов уже находящихся на предприятии:

Так как 2-ой и 3-ий ресурсы расходуются полностью, то и больше 0.

Мы получили математическую модель задачи «расшивки узких мест»:

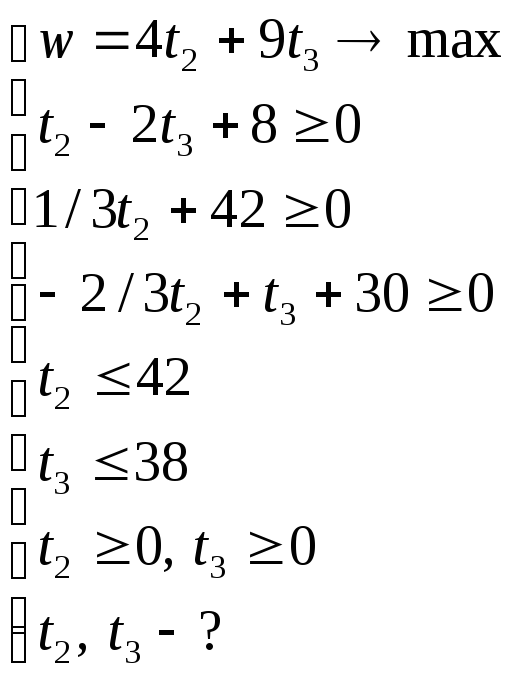
Решим задачу графически:

Так как , то можно исключить из системы:

где 1 - , 2 - , 3 - , 4 - 5 – градиент целевой функции , 6 – линия уровня, заштрихованная область – область допустимых решений, т.е. значения и , при которых выполняются ограничения. ОДР образует многоугольник. Передвигая линию уровня по направлению градиента, мы пройдём все вершины многоугольника ОДР. Последняя вершина будет соответствовать максимальному значению целевой функции. В данном случае это точка А с координатами (42;25) ( и ). Область устойчивости находится между и прямыми (двойная штриховка).

Программа расшивки имеет вид: (0, 42, 25), а прирост прибыли составляет

Задание №4

ТРАНСПОРТНАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Имеется 3 производителя однородной продукции, имеющие запасы этой продукции 65, 40 и 70 единиц соответственно. Также имеется 4 потребителя данной продукции. Их потребность составляет 30, 58, 32 и 43 единицы соответственно. Транспортная компания заключила контракт с поставщиками и потребителями на вывоз и поставку данной продукции от производителей к потребителям. При перевозке продукции от каждого производителя к каждому потребителю транспортная компания имеет определённые издержки на единицу продукции: 1 у.е. при перевозке от 1-ого производителя к 1-ому потребителю, 3 у.е. - от 1–ого производителя ко 2-ому потребителю, 2 у.е. – от 1-ого к 3-ему, 5 у.е. – от 1-ого к 4-ому, 4 у.е. – от 2-ого к 1-ому, 6 у.е. – от 2-ого ко 2-ому, 5 у.е. – от 2-ого к 3-ему, 9 у.е. – от 2-ого к 4-ому, 2 у.е. – от 3-его к 1-ому, 4 у.е. – от 3-его ко 2-ому, 1 у.е. – от 3-его к 3-ему, 3 у.е. – от 3-его к 4-ому. Так как естественным стремлением транспортной компании является максимизация прибыли, то требуется составить такой план перевозок, чтобы издержки были минимальными.

Можно записать эти издержки на единицу продукции в виде матрицы, где строка издержки при поставке от одного производителя к каждому потребителю, а столбец издержки при поставке к одному потребителю от каждого производителя:

Предложение производителей и спрос потребителей можно записать в виде векторов А и B соответственно:

и

Суммарное предложение не больше суммарного спроса. Для того, чтобы они были равны введём фиктивного потребителя с потреблением равным разнице между предложением и спросом.. Фактически эта потребность будет указывать на количество продукции, которая не будет вывозиться от производителя. Для того, чтобы введение фиктивного потребителя не повлияло на решение, затраты на перевозку единицы продукции к фиктивному потребителю приравняем к 0. В действительности это будет также, так как транспортная компания не будет нести издержки за товар, который она никуда не возит. Тогда вектор В и матрица С будут выглядеть так:

и

Мы получили так называемую «замкнутую» задачу.

Обозначим количество перевезённой продукции за x. Таким образом, количество перевезённой продукции от 1-ого производителя к 1-ому потребителю будет , а от 1-ого производителя ко 2-ому потребителю - и т.д. Мы получим матрицу одного размера с С:

Так как нам требуется найти план перевозок, т.е. такие x, чтобы суммарные издержки были минимальными, то выражение

,

значение которого и есть суммарные издержки (т.е. количество перевезённой продукции помноженное на соответствующие издержки на единицу продукции из матрицы С), должно быть минимальным.

С другой стороны, суммарные перевозки от одного производителя должны быть равны его запасам, а суммарные перевозки к одному потребителю должны быть равны его потреблению:

Кроме того, все количество перевозимой продукции по смыслу задачи должно быть положительной.

Итак, математическая модель нашей задачи:

Это задача линейного программирования. Решим её методом потенциалов. Составляется таблица, которая соответствует матрице X. Для решения требуется первое базисное решение. Найдем его с помощью метода минимальных издержек: выбирается 1-ая базисная переменная соответствующая минимальным издержкам, ей присваивается максимально возможное значение; потом выбирается по тому же критерию 2-ая базисная переменная среди оставшихся и т.д.

	30	58	32	43	12
65	30 1	35 3	-- 2	-- 5	-- 0
40	-- 4	23 6	-- 5	5 9	12 0
70	-- 2	-- 4	32 1	38 3	-- 0

где «--» соответствует свободным переменным, а числа в нижнем правом углу ячейки – соответствующим издержкам.

Пусть p и q – двойственные переменные, соответствующие строкам и столбцам таблицы. Если значения x, p и q - допустимые решения соответствующих двойственных задач, то при равенстве целевых функций эти решения – оптимальны. Для того чтобы целевые функции были равны требуется выполнение условий: для базисных переменных и для свободных переменных (). Таким образом, для нашей таблицы получим систему:

Пусть , тогда - это допустимое решение.

Тогда - решение не оптимально т.к. есть .

Так как решение не оптимально поменяем набор базисных переменных. Для этого выберем ячейку, которой соответствует максимальная симплекс-разница . Для того, чтобы не нарушить равновесия воспользуемся методом циклического пересчёта:

	30	58	32	43	12
65	30 1	35 3	-- 2	-- 5	-- 0
40	-- 4	23 6	+w--5	-w5 9	12 0
70	-- 2	-- 4	-w321	+w383	-- 0

где w=5. Таким образом, сумма в строках и столбцах осталась неизменной, а мы получили новое базисное решение:

	30	58	32	43	12
65	30 1	35 3	-- 2	-- 5	-- 0
40	-- 4	23 6	5 5	-- 9	12 0
70	-- 2	-- 4	27 1	43 3	-- 0

Проверим его на оптимальность:

- решение оптимально, так как все симплекс разницы

Ответ: при 12 единицах продукции оставшихся у 2-ого производителя.

Задача №5

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ. РАСПРЕДЕЛЕНИЕ КАПИТАЛЬНЫХ ВЛОЖЕНИЙ

Динамическое программирование - это вычислительный метод для решения задач управления определённой структуры. Данная задача с n переменными представляется как много шаговый процесс принятия решений. На каждом шаге определяется экстремум функции только от одной переменной.

Рассмотрим нелинейную задачу распределения ресурсов между предприятиями отрасли.

Имеются n пунктов, где требуется построить или реконструировать предприятия одной отрасли, для чего выделено b рублей. Обозначим через f_j(x_j) прирост мощности или прибыли на j-том предприятии, если оно получит x_j рублей капвложений. Требуется найти такое распределение (х₁, х₂, ..., х_n) капвложений между предприятиями, которое максимизирует суммарный прирост мощности или прибыли

Z=f₁(x₁)+f₂(x₂)+...+f_n(x_n)

при ограничении по общей сумме капвложений

х₁ + х₂ +...+х_n = b

причём будем считать, что все переменные x_j принимают только целые значения x_j =1,2,...

Функции f_j(x_j) мы считаем заданными, заметив, что их определение - довольно трудоёмкая экономическая задача.

Воспользуемся методом динамического программирования для решения этой задачи.

Введём параметр состояния и определим функцию состояния. За параметр состояния  примем количество рублей, выделяемых нескольким предприятиям, а функцию состояния F_k() определим как максимальную прибыль на первых k предприятиях, если они вместе получат  рублей. Параметр  может меняться от 0 до b. Если из  рублей k-ое предприятие получит Х_к рублей, то каково бы ни было это значение, остальные -Х_к рублей естественно распределить между предприятиями от 10-го до (к-1)-го предприятия, чтобы была получен максимальная прибыль F_k-1(-x_k). Тогда прибыль k предприятий будет равна f_k(x_k) + F_k-1(-x_k). Надо выбрать такое значение x_k между 0 и , чтобы эта сумма была максимальной, и мы приходим к рекуррентному соотношению:

F_k() = max {f_k(x_k) + F_k-1(-x_k)}

0  X  

для k=2,3,....,n .Если же k=1 ,то

F₁()=f₁().

Рассмотрим конкретный пример. Пусть производственное объединение состоит из 4-х предприятий (n=4).Общая сумма капвложений равна 700 тыс. рублей (b=700) , выделяемые предприятиям суммы кратны 100 тыс. рублей.

Значения функций f_j(x_j) приведены в табл. 1.

Таблица 1.

Xj	0	100	200	300	400	500	600	700
f1(xj)	0	5	10	14	17	19	21	22
f2(xj)	0	20	34	45	50	48	40	40
f3(xj)	0	15	24	30	38	46	52	53
f4(xj)	0	26	30	35	40	45	48	50

Прежде всего заполняем табл.2. Значения f₂(x₂) складываем со значениями F₁(-x₂)=f₁(-x₂) и на каждой северо-восточной диагонали находим наибольшее число, которое помечаем звёздочкой и указываем соответствующее значение ₂ (). Заполняем табл .3.

Таблица 2.

х2	-х2	0	100	200	300	400	500	600	700
	F1(-x2) f2(x2)	0	5	10	14	17	19	21	22
0	0	0	5	10	14	17	19	21	22
100	20	20*	25	30	34	37	39	41	---
200	34	34*	39	44	48	51	53	---	---
300	45	45*	50*	55*	59	62	---	---	---
400	50	50*	55*	60*	64*	---	---	---	---
500	48	48	53	58	---	---	---	---	---
600	40	40	45	---	---	---	---	---	---
700	40	40	---	---	---	---	---	---	---

Таблица 3.

	0	100	200	300	400	500	600	700
F2()	0	20	34	45	50	55	60	64
x2()	0	100	200	300	300	400	400	400

Продолжая процесс, табулируем функции F₃(), x₃() и т.д.

Таблица 4.

x3	-х3	0	100	200	300	400	500	600	700
	F2(-x3) f3(x3)	0	20	34	45	50	55	60	64
0	0	0	20*	34	45	50	55	60	64
100	15	15	35*	49*	60*	65	70	75	---
200	24	24	44	58	69*	74	79	---	---
300	30	30	50	64	75*	80	---	---	---
400	38	38	58	72	83*	---	---	---	---
500	46	46	66	80	---	---	---	---	---
600	52	52	72	---	---	---	---	---	---
700	53	53	---	---	---	---	---	---	---

Таблица 5.

	0	100	200	300	400	500	600	700
F3()	0	20	35	49	60	69	75	83
x3()	0	0	100	100	100	200	300	400

В табл.6 заполняем только одну диагональ для значения =700.

Таблица 6.

x4	-х4	0	100	200	300	400	500	600	700
	F4(-x4) f4(x4)	0	20	35	49	60	65	75	83
0	0								83
100	26							101	---
200	30						99	---	---
300	35					95	---	---	---
400	40				89	---	---	---	---
500	45			80	---	---	---	---	---
600	48		68	---	---	---	---	---	---
700	50	50	---	---	---	---	---	---	---

Наибольшее число на этой диагонали:

P_max = 101 тыс. руб.,

Причем четвертому предприятию должно быть выделено:

х^*₄ = ₄ (700) = 100 тыс. руб.

На долю остальных трех предприятий остается 600 тыс. руб. Из табл. 5 видно, что третьему предприятию должно быть выделено

x^*₃ = ₃ (700-x^*₄) = ₃ (600) = 300 тыс. руб.

Продолжая обратный процесс, находим

x*₂ = ₂ (700 - x*₄ - x*₃) = ₂ (300) = 300 тыс. руб.

На долю первого предприятия остается

x*₁ = 700 - x*₄ - x*₃ - x*₂ = 0 тыс. руб.

Оптимальная программа:

Х1*=0; Х2*=100; Х3*=300; Х4*=300

P_max(X1*;... X4*) = 0+45+30+26 = 101,

так как выполнилось равенство, эта программа оптимальна.

Ответ: оптимальная производственная программа имеет вид:

Х1* = 0; Х2* = 100; Х3* = 300; Х4* = 300 , при этом максимальная прибыль составляет 35 тыс. руб.

Задание №6

АНАЛИЗ ДОХОДНОСТИ И РИСКА ФИНАНСОВЫХ ОПЕРАЦИЙ

Финансовой называется операция, начальное и конечное состояния которой имеют денежную оценку и цель проведения которой заключается в максимизации дохода – разности между конечной и начальной оценками.

Почти всегда финансовые операции проводятся в условиях неопределенности, и потому их результат невозможно предсказать заранее. Поэтому финансовые операции рискованны, т.е. при их проведении возможны как прибыль, так и убыток.

Существует несколько разных способов оценить операцию с точки зрения ее доходности и риска. Наиболее распространенным является представление дохода операции как случайной величины и оценка риска операции как среднего квадратического отклонения этого случайного дохода.

Рассмотрим какую-нибудь операцию, доход которой есть случайная величина . Средний ожидаемый доход – это математическое ожидание с.в. : , где есть вероятность получить доход . А среднее квадратическое отклонение (СКО) – это мера разбросанности возможных значений дохода вокруг среднего ожидаемого дохода. Вполне разумно считать количественной мерой риска операции и обозначать . Таким образом, здесь предлагается новый количественный измеритель риска операции. В финансовой математике этот измеритель считается основным. Напомним, что дисперсия с.в.:

.

Рассмотрим четыре операции . Найдем средние ожидаемые доходы и риски операций.

Ряды распределения, средние ожидаемые доходы и риски:

QQ1:	00	88	116	220
	11/2	11/8	11/8	11/4

₁ =8 r₁ = 8,71

QQ2:	22	112	118	222
	11/2	11/8	11/8	21/4

₂ =10,25 r₂ = 8,74

QQ3:	00	44	110	114
	11/4	11/4	11/4	21/4

₃ = 7 r₃ = 5,38

QQ4:	22	16	512	120
	11/4	21/4	11/4	11/4

₄ = 10 r₄ = 6,78

Напомним, как находить и r.

= 0*1/2+8*1/8+16*1/8+20*1/4=8

r₁² = 0*1/2+64*1/8+256*1/8+400*1/4=140

r₁ = √140-64 = 8,71

Нанесем средние ожидаемые доходы и риски r на плоскость.

Получили 4 точки. Чем выше точка , тем более она рисковая операция, чем точка правее – тем более она доходная. Значит, нужно выбирать точку правее и ниже. Точка доминирует точку , если и и хотя бы одно из этих неравенств строгое.

Точка, не доминируемая никакой другой, называется оптимальной по Парето, а множество всех таких точек называется множеством оптимальности по Парето. Легко видеть, что если из рассмотренных операций надо выбирать лучшую, то ее обязательно надо выбрать из операций по Парето.

Для большей достоверности можно применить подходящую взвешивающую формулу. Например, пусть взвешивающая формула есть прежняя . Тогда получаем:

φ(Q₁) = 2*8-8,71= 7,29; φ(Q₂) = 11,76; φ (Q₃) = 8,62; φ (Q₄) = 13,22. Видно, что 4-я операция – лучшая, а 1-я – худшая.

Задание №7

ЗАДАЧА ФОРМИРОВАНИЯ ОПТИМАЛЬНОГО ПОРТФЕЛЯ ЦЕННЫХ БУМАГ

На финансовом рынке обращается, как правило, множество ценных бумаг. Из характеристик ценных бумаг наиболее значимы две: эффективность и рискованность. Эффективность Е есть некоторый обобщенный показатель дохода и прибыли. Будем считать Е случайной величиной, ее математическое ожидание есть m_E.

При исследовании финансового рынка дисперсию обычно называют вариацией V и рискованность обычно отождествляется со Средним Квадратическим Отклонением. Т.о., V=D[E] =M[(E - m_E )² и = √V

Сформировать оптимальный портфель заданной эффективности из трех видов ценных бумаг: безрисковых эффективности 2 и некоррелированных рисковых ожидаемой эффективности 4 и 6 и рисками 6 и 8.

x_i - доля капитала, потраченная на закупку ценных бумаг i-го вида,

m₀ - эффективность безрисковых бумаг

x₀ - доля капитала, вложенного в безрисковые бумаги

m_r - средняя ожидаемая эффективность рисковой части портфеля

(1-x₀) - вложено в рисковую часть портфеля всего капитала

m_p =x₀ m₀ +(1-x₀ )m_{r -} ожидаемая эффективность всего портфеля

x₀ m₀ + = m_p x₀ + =1

V - матрица ковариаций рисковых видов ценных бумаг,

X=(x_i), M=(m_i) - векторы-столбцы долей x_i капитала, вкладываемых в i-й вид рисковых ценных бумаг и ожидаемых эффективностей этого вида, i=1,.., n;

I - n-мерный вектор-столбец, компоненты которого есть 1.

Тогда оптимальное значение долей x_i есть

.

m₀ =2, M= 4 , V= 36 0 m_p - эффективность портфеля

6 0 64

Теперь надо найти обратную матрицу к матрице V:

обратная матрица к матрице V: V^-1 = 1/36 0

0 1/64

Знаменатель матрицы:

V^-1 (M– m₀I)= 1/36 0 * 2 = 1/18

0 1/64 4 1/16

(M– m₀I)^T V^-1 (M– m₀I)=(2 4)* 1/18 = 13/36

1/16

вектор долей рисковых бумаг X^* =(36(m_р - 2)/13) 1/18

1/16

Рисковые доли должны быть одинаковы и каждая из них равна (36(m_р - 2)/13). Следовательно, x₀* = 1 - (36(m_р - 2)/13).

Необходимость в операции "short sale" возникнет, если x^*₀ < 0, т.е. когда m_р > 2,36 .

Риск оптимального портфеля в зависимости от его доходности при наличии безрисковых бумаг равен , где

Таким образом, d =√13/36 = 0,6, а риск r = (m_р - 2)/ 0,6.

24