Математический маятник

 

Математический маят­ник — это материальная точка, подвешенная на невесомой и нерас­тяжимой нити, находящейся в поле тяжести Земли. Математический маятник — это идеализированная модель, правильно описывающая реальный маятник лишь при определенных условиях. Реальный ма­ятник можно считать математическим, если длина нити  много больше размеров подвешенного на ней тела, масса нити ничтожна мала по сравнению с массой тела, а деформации нити настолько малы, что ими вообще можно пренебречь.

Колебательную систему в данном случае образуют нить, присо­единенное к ней тело и Земля, без которой эта система не могла бы служить маятником.

,

где а_х – ускорение, g – ускорение свободного падения, х - смещение, l – длина нити маятника.

Это уравнение называется урав­нением свободных колебаний математического маятника.  Оно правильно описывает рассматриваемые колебания лишь тогда, когда выполнены следующие предположения:

1)  будем считать, что силы трения, действующие на тело, пре­небрежимо малы и потому, их можно не учитывать;

2)   рассматриваются лишь малые колебания маятника с небольшим углом размаха.

Свободные колебания любых систем во всех слу­чаях описываются аналогичными уравнениями.

Причинами свободных колебаний математическо­го маятника являются:

1.  Действие на маятник силы натяжения и силы тяжести, пре­пятствующей его смещению из положения равновесия и заставляю­щей его снова опускаться.

2. Инертность маятника, благодаря которой он, сохраняя свою скорость, не останавливается в положении равновесия, а проходит через него дальше.

Период свободных колебаний математического ма­ятника

.

Период свободных колебаний математического маятника не за­висит от его массы, а определяется лишь длиной нити и ускорением свободного падения в том месте, где находится маятник.

 

 

Превращение энергии при гармонических колебаниях

 

При гармонических колебаниях пружинного маятника проис­ходят превращения потенциальной энергии упруго деформированного телав его кинетическую энергию , гдеk – коэффициент упругости,х - модуль смещения маятника из поло­жения равновесия,m- масса маятника,v- его скорость. В соот­ветствии с уравнением гармонических колебаний:

, .

Полная энергия пружинного маятника:

.

Полная энергия для математического маятника:

В случае математического маятника

Превращения энергии при колебаниях пружинного маятника происходи в соответствии с законом сохранения механической энергии (). При движении маятника вниз или вверх от положения равновесия его потенциальная энергия увеличивается, а кинетическая - уменьшается. Когда маятник проходит положение равно­весия (х = 0), его потенциальная энергия равна нулю и кинетическая энергия маятника имеет наибольшее значение, равное его полной энергии.

Таким образом, в процессе свободных колебаний маятника его потенциальная энергия превращается в кинетическую, кинетическая в потенциальную, потенциальная затем снова в кинетическую и т. д. Но полная механическая энергия при этом остается неизменной.

 

Вынужденные колебания. Резонанс.

 

Колебания, происходящие под действием внеш­ней периодической силы, называются вынужден­ными колебаниями. Внешняя периодическая си­ла, называемая вынуждающей, сообщает колеба­тельной системе дополнительную энергию, которая идет на восполнение энергетических потерь, проис­ходящих из-за трения. Если вынуждающая сила изменяется во времени по закону синуса или коси­нуса, то вынужденные колебания будут гармониче­скими и незатухающими.

В отличие от свободных колебаний, когда система получает энергию лишь один раз (при выведении системы из со­стояния равновесия), в случае вынужден­ных колебаний система поглощает эту энергию от источника внешней периоди­ческой силы непрерывно. Эта энергия восполняет потери, расходуемые на пре­одоление трения, и потому полная энергия колебательной системы no-прежнему ос­тается неизменной.

Частота вынужденных колебаний равна часто­те вынуждающей силы. В случае, когда частота вынуждающей силы υ совпадает с собственной ча­стотой колебательной системы υ₀, происходит рез­кое возрастание амплитуды вынужденных колеба­ний — резонанс. Резонанс возникает из-за того, что при υ = υ₀  внешняя сила, действуя в такт со свободными колебаниями, все время сонаправлена со скоростью колеблющегося тела и совершает по­ложительную работу: энергия колеблющегося те­ла увеличивается, и амплитуда его колебаний ста­новится большой. График зависимости амплитуды вынужденных колебаний А_т от частоты вынужда­ющей силы υ  представлен на рисунке, этот график называется резонансной кривой:

 

 

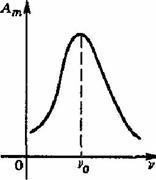
Явление резонанса играет большую роль в ря­де природных, научных и производственных про­цессов. Например, необходимо учитывать явление резонанса при проектировании мостов, зданий и других сооружений, испытывающих вибрацию под нагрузкой, в противном случае при определенных условиях эти сооружения могут быть разрушены.