- •Структура рабочей тетради
- •Введение Пояснительная записка
- •Тематический план
- •Рекомендации по работе с математическим текстом
- •Рекомендации по конспектированию
- •Рекомендации по решению задач
- •Раздел 1. Теория пределов
- •Предел функции
- •Первый и второй замечательные пределы.
- •- Второй замечательный предел
- •Непрерывность функции Непрерывность функции в точке
- •Односторонние пределы функции*
- •Точки разрыва и их классификация*
- •Устранимый разрыв
- •Вопросы для самоконтроля
- •Контрольные задания
- •Раздел 2. Дифференциальное исчисление функции одной переменной
- •Производная функции одной переменной. Правила дифференцирования. Производная сложной функции
- •Геометрический смысл производной
- •Механический смысл производной
- •Правила дифференцирования
- •Формулы дифференцирования
- •Производная сложной функции
- •Дифференциал
- •Производные и дифференциалы высших порядков
- •Исследование функции при помощи дифференциального исчисления
- •Вопросы для самоконтроля
- •Контрольное задание
- •Раздел 3. Интегральное исчисление функции одной переменной
- •Первообразная функции. Неопределенный интеграл и его свойства.
- •Приемы интегрирования
- •Вопросы для самоконтроля
- •Контрольное задание
- •Определенный интеграл
- •Геометрические приложения определенного интеграла
- •Вопросы для самоконтроля
- •Контрольное задание
- •Раздел 4. Ряды
- •Основные понятия
- •Необходимый признак сходимости ряда. Достаточные признаки сходимости рядов с положительными членами.
- •Знакопеременные и знакочередующиеся ряды. Абсолютная и условная сходимость. Признак Лейбница для знакочередующихся рядов.
- •Вопросы для самоконтроля
- •Контрольное задание
- •Раздел 5. Основы теории вероятностей и математической статистики.
- •Основные понятия комбинаторики
- •Вопросы для самоконтроля
- •Контрольное задание
- •Классическое определение вероятности
- •Вопросы для самоконтроля
- •Контрольное задание
- •Случайные величины
- •Числовые характеристики случайной величины
- •Вопросы для самоконтроля
- •Контрольное задание
- •Литература
Предел функции
Определение предела функции в точке
Сформулируем определение предела функции в точке.
Определение. Пусть функция f(x) определена в некоторой окрестности точки а, кроме, может быть, самой точки а, Число В называется пределом функции f(x) в точке а (или при х, стремящемся к а), если для любой последовательности значений аргумента хп ¹ а, п Î N, сходящейся к а, последовательность соответствующих значений функции f(xп), п Î N, сходится к числу В.
В этом случае пишут:![]() или
или
![]() при
при
![]() .
.
Если же для некоторой последовательности значений аргумента, сходящейся к а, соответствующая последовательность значений функции не является сходящейся, то функция в данной точке не имеет предела. То же заключение можно сделать, если для двух различных последовательностей значений аргумента последовательности соответствующих значений функции имеют различные пределы.
Очевидно, число Вявляется пределом
функции
![]() при
при![]() тогда и только тогда, когда
тогда и только тогда, когда
![]() можно представить в виде:
можно представить в виде:
![]() =В+
=В+
![]() ,
где
,
где
![]() при
при![]() .
.
Отметим,
что точка а, в которой рассматривается
предел функции
![]() ,
может принадлежать области определения
функции
,
может принадлежать области определения
функции
![]() ,
а может и не принадлежать. При нахождении
предела функции в точке не рассматривается
значение функции в этой точке.
,
а может и не принадлежать. При нахождении
предела функции в точке не рассматривается
значение функции в этой точке.
Пример.Докажем справедливость следующих равенств:
1)
![]() ,
при
,
при
![]() = с; 2)
= с; 2)
![]() при
при
![]() .
.
Решение.
Пусть
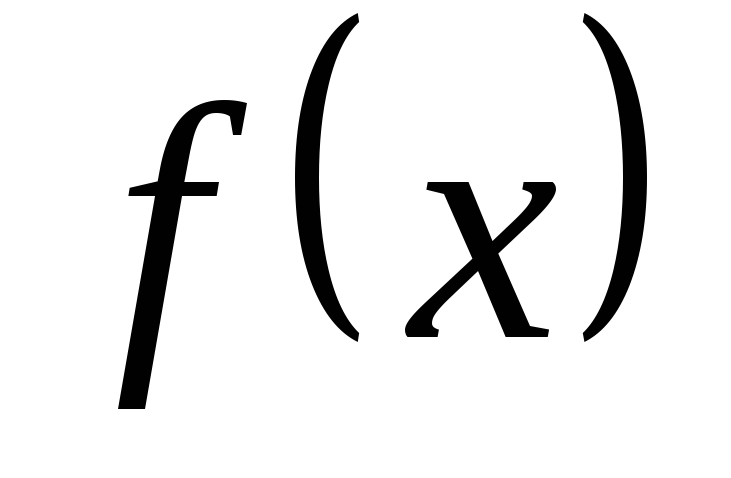 =сдля всеххиз некоторого
интервала, содержащего точкуа.
Тогда для любой последовательности(хn)такой, чтохn
® априn®¥, имеем
=сдля всеххиз некоторого
интервала, содержащего точкуа.
Тогда для любой последовательности(хn)такой, чтохn
® априn®¥, имеем
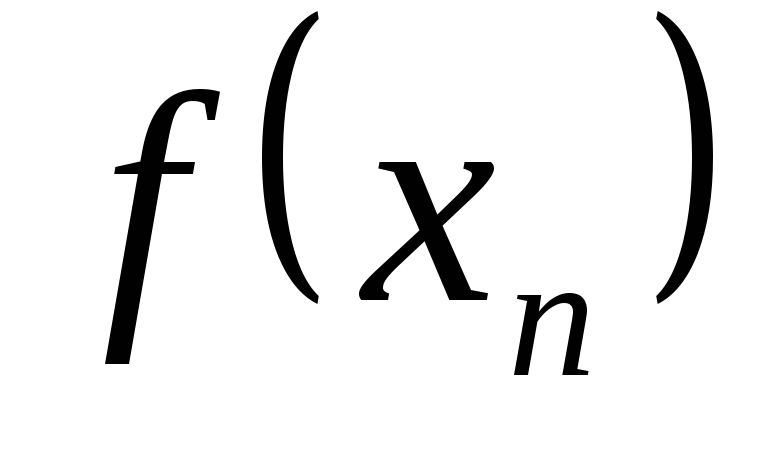 =си
=си
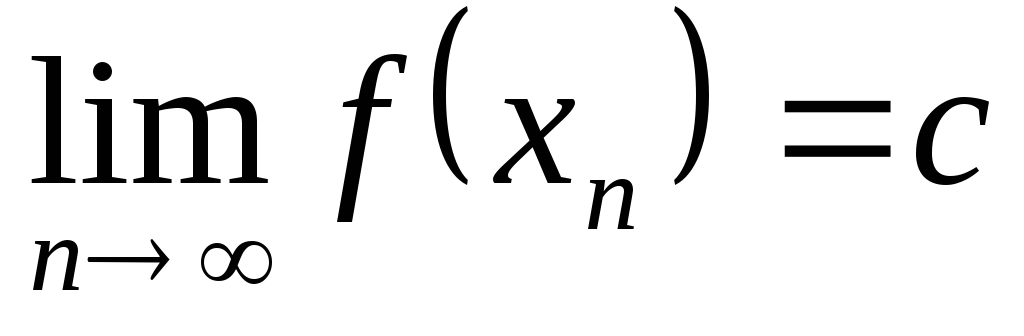 .
.
Следовательно
![]() .
.
Для любой последовательности (хn)такой, чтохn ® априn®¥, имеем
![]() .
.
Следовательно, согласно определению
предела
![]() .
.
Свойства пределов функций
Основные свойства пределов функций аналогичны теоремам о пределах числовых последовательностей:
1) Предел суммы (разности) функций равен
сумме (разности) их пределов, если
последние существуют:
![]() .
.
2) Предел произведения функций равен
произведению их пределов, если последние
существуют:
![]() .
.
Следствие.Постоянный множитель
можно выносить за знак предела:
![]() ,
если
,
если
![]() существует.
существует.
3) Предел отношения двух функций равен
отношению их пределов, если последние
существуют и предел делителя отличен
от нуля:
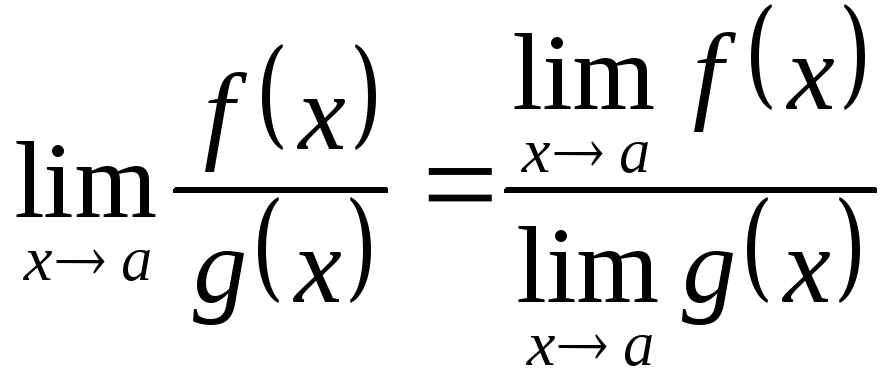 ,
если
,
если
![]() .
.
При изучении пределов функций иногда полезно использовать следующую «теорему о пределе промежуточной функции».
Теорема.Если
![]() ,
,
![]() и в некоторой окрестности точкиа,
кроме, быть может, самой точкиа,
выполняются неравенства
и в некоторой окрестности точкиа,
кроме, быть может, самой точкиа,
выполняются неравенства![]() ,
то
,
то
![]() .
.
Пример.Вычислите пределы фукций:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)![]() .
.
Решение.
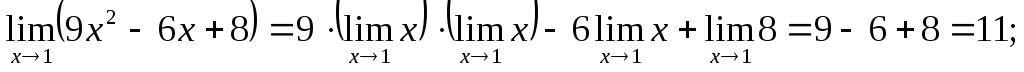
Поскольку предел знаменателя равен 0, то воспользоваться теоремой о пределе частного невозможно. Поэтому первоначально сократим дробь, разложив числитель на множители:
![]()
Ответ.1) 11, 2) –1, 3) 2.
Задание. Вычислите пределы функций:
1).![]()
Решение:
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Ответ:-1
2).![]()
Решение:
______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________Ответ:-6.
Определение предела функции на бесконечности
При изучении свойств функции приходится рассматривать предел функции в бесконечности, бесконечный предел функции в точке, а также бесконечный предел в бесконечности.
Рассмотрим
более подробно предел функции в
бесконечности, т.е. при
![]() и при
и при![]() .
.
Определение. Пусть функция
f(x)
определена на всей числовой прямой.
Число В называется пределом
f(x)
при
![]() ,
если
,
если
![]() для любой последовательности (хп)
такой, что
для любой последовательности (хп)
такой, что
![]() .
.
В этих случаях пишут, что
![]() .
Аналогично,
.
Аналогично,
![]() ,
если
,
если
![]() для любой последовательности (хп)
такой, что
для любой последовательности (хп)
такой, что
![]() .
.
Пример.Докажем, что
![]()
Решение.
Рассмотрим произвольную последовательность (хп) такую, что
![]() .
.
Так как последовательность
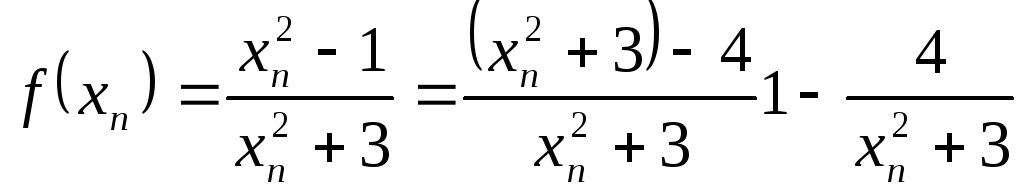 ,
гдеn Î N,
сходится к 1, то согласно определению
,
гдеn Î N,
сходится к 1, то согласно определению
![]() .
Легко видеть, что и
.
Легко видеть, что и
![]() .
.
Кроме рассмотренного случая конечного
предела функции f(x)
прих®∞ (или иначех®±¥)
используется понятие бесконечного
предела. Например, функция![]() ,
определенная для всехх¹0, принимает сколь угодно большие значения
прих®0. В этом случае говорят, что функция в
точкех= 0 имеет своим пределом
бесконечность, и пишут
,
определенная для всехх¹0, принимает сколь угодно большие значения
прих®0. В этом случае говорят, что функция в
точкех= 0 имеет своим пределом
бесконечность, и пишут![]() .
.
Определение. Если для любой
последовательности значений аргумента
(хп)
такой, что хп ¹ 0
и
![]() ,
имеет место
,
имеет место
![]() ,
то говорят, что предел функции f(x)
в точке а есть бесконечность,
и пишут
,
то говорят, что предел функции f(x)
в точке а есть бесконечность,
и пишут
![]() .
.
Пример. Найдите пределы функций:
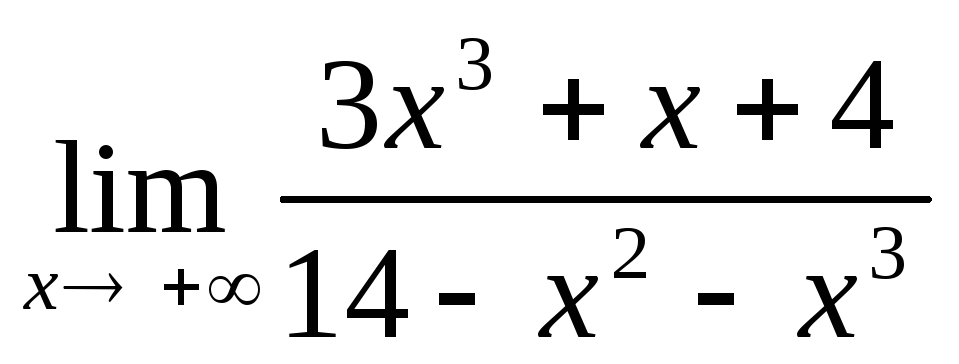 ;2)
;2)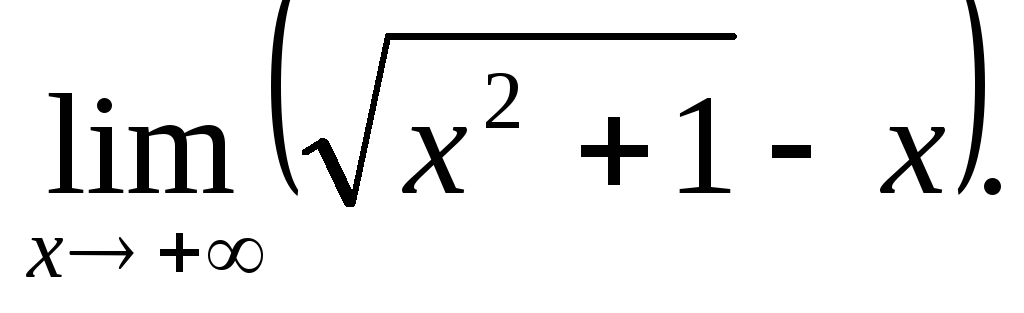
Решение. При определении значений предела функции на бесконечности воспользуемся тем же приемом, что и в случае последовательности:
Ответ.1) -3, 2) 0.
Задание. Вычислите предел функции на бесконечности:
![]()
Решение:
____________________________________________________________________________________________________________________________________
Ответ:-1.