Приклади дискретних розподілів.
1. Біноміальний розподіл.
Нехай
зроблено n
незалежних випробувань. У кожному
випробуванні настає або подія А, або
відповідно з ймовірностями р, 1 -р.
Розглянемо випадкову величину
- число появ події А в послідовності
випробувань.
Закон розподілу цієї випадкової величини можна записати таким чином
Р
(
= m) =
,
m=0,1,2,…n...
(4)
Дійсно, розглянемо вираз (p + q)n =1 , розкладемо двочлен (p + q)n за формулою бінома Ньютона. Одержимо
тобто сума ймовірностей значень випадкової величини дорівнює одиниці, отже (4) є законом розподілу.
Знайти
математичне сподівання
за
означенням, тобто за формулою
M
()
=
,
дуже складно.
Тому розглянемо випадкові величини 1, 2, … n , с однаковим законом розподілу :
k
=
де k = 1,2,...n . Тоді
= 1 + 2 + … + n...
Використовуючи властивості математичного сподівання одержимо:
М () = М (1 + 2 + … + n) = М (1) + М (2) +…+М (n) .
Знайдемо математичне сподівання k ,
М
(k)
= 0 · (1 - p) + 1· p = р,
, тоді
М () = np
Аналогічно знайдемо дисперсію:
D () = D (1 + 2 + … + n) = D (1) + D (2) +…+ D (n)
D (k) = (0 – p)2 (1 – p) + (1 – p)2 p = p2 (1 – p) + (1 – p)2 p = p (1 - p) (p + 1 - p) = p (1 - p) = p q
D () = n p q,
2. Розподіл Пуассона.
Нехай зроблено нескінченне число випробувань. Розглянемо випадкову величину -число появ події А.
Закон розподілу в цьому випадку має вигляд:
p
(
=m) =
,
λ > 0 - параметр розподілу, m = 0, 1, 2,
... (5)
Покажемо, що сума ймовірностей дорівнює одиниці.
.
Аналогічно
можна показати, що математичне сподівання
й дисперсію відповідно рівні
,
М
()
=
,D ()
=
.
Закон Пуассона називають законом рідких подій.
Лекція 7,8.
Неперервні випадкові величини.
Щільність розподілу .
Щільність
розподілу ймовірностей f(x) характеризує
ймовірність попадання випадкової
величини в деякий інтервал. Ця ймовірність
дорівнює площі фігури, розташованої
між віссю абсцис і графіком функції
f(x) на інтервалі
(
Рисунок 8). Зазначимо, що функція f(x)
=
.
Рисунок 8. Щільність розподілу ймовірностей f(x)
Щільність розподілу має наступні властивості:
1. f (x) >0
2.
3.
p( a
4.
f(x) =
в точках неперервності функції f(x).
Поняття функції розподілу, математичного сподівання й дисперсії мають такий же смисл, як у дискретному випадку, а обчислюються відповідно за формулами (6) - (8).
(6)
M
()
=
(7)
D()
=
(8)
Приклад
13. Випадкова величина
,
що розподілена за законом , який
визначається щільністю розподілу
ймовірностей виду
f
(x) =
Знайти параметр a, F(x), M () , D() .
Параметр
a
знайдемо із властивості
,
інтеграл
розіб'ємо
на суму трьох інтегралів
Намалюємо графік щільності розподілу f (x) (Рисунок 9)
Рисунок 9. Графік щільності розподілу f (x)
Обчислимо
функцію розподілу, для цього розглянемо
інтервали
.
1.
х
(- ∞, 0)
,
2.
х
[0, 2]
,
3.
х
(2,
)
.
Графік функції наведений на Рисунку 10.
Обчислимо математичне сподівання й дисперсію:
Рисунок 10. Графік функції розподілу.
Модою випадкової величини неперервного типу Md, називається дійсне число - точка максимуму щільності розподілу ймовірностей f(x).
Медіаною випадкової величини неперервного типу Mn називається дійсне число, що задовольняє рівняння
F(x)
=
.
Квантилью
порядка р
розподілу
випадкової величини
неперервного типу називається дійсне
число
,
що задовольняє рівняння р
= р
Приклади розподілів безперервної випадкової величини.
Рівномірний розподіл.
Випадкова величина неперервного типу називається розподіленою рівномірно на відрізку [a,b], якщо її щільність розподілу має від:
f(x)
=
(9)
Обчислимо
математичне сподівання й дисперсію:
,
=
Розглянутий в Прикладі 13 розподіл є рівномірним при a = 0 і b = 1.
2. Показниковий (експонентний) розподіл:
Випадкова
величина
називається розподіленою за показниковим
(експонентним)
законом з параметром
>0,
якщо вона неперервного типу і її щільність
розподілу задається формулою
f(x)
=
(10)
Графік функції наведений на Рисунку11.
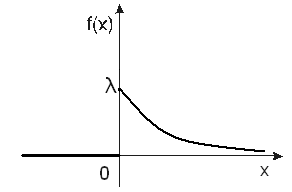
Рисунок 11. Щільність показового (експонентного) розподілу
Математичне сподівання й дисперсія відповідно рівні:
M
()
=
,D ()=
3. Закон нормального розподілу.
Випадкова
величина називається розподіленою за
нормальним законом з параметрами а
й
>0,
якщо щільність розподілу ймовірностей
має вигляд
f(x)
=
,
(11)
Для того, щоб побудувати графік цієї функції, проведемо її дослідження. Обчислимо похідну
.
При
x < a
>
0, отже на інтервалі
функція зростає, а при x >a
< 0, - функція спадає. У точці x =a
– функція
має максимум.
Графік
функції наведений на Рисунку 12.
Важливе
значення в прикладних задачах має
окремий випадок щільності нормального
розподілу при a
= 0 і
=1
.
(12)
Це, так званий, стандартний нормальний розполіл. Функція (12) - парна , тобто
(-x)
=
(x).
Для значень цієї функції є таблиці ( Додаток 1).
Рисунок 12. Щільність нормального розподілу.
Обчислимо математичне сподівання й дисперсію:
;
;
.
При обчисленні інтегралів використані властивості:
1)
=
0, як інтеграл від непарної функції в
симетричних межах;
2)
=1, як інтеграл від щільності нормального
розподілу з параметрамиa
= 0 і
=
1 ( властивість 2 функції щільності
розподілу).
Аналогічно
можна показати, що D ()
=
2
. Параметри a і
збігаються з основними характеристиками
розподілу. Надалі, якщо щільність
розподілу випадкової величини має
вигляд (11), то для стислості будемо
записувати
~ N (
).
Ймовірність
попадання випадкової величини
в інтервал
обчислюється за формулою
,
(13)
де
-
функція Лапласа
,
(14)
функція нормального розподілу N(0,1), для цієї функції є таблиці (Додаток 2).
Відзначимо, що
Ф(-x) = 1 - Ф(x) (15)
Приклад 14. Коробки із шоколадом упаковують автоматично. Їхня середня маса дорівнює 1,06 кг. Відомо, що 5 % коробок мають масу менше 1 кг. Який відсоток коробок, маса яких перевищує 940 р. (вага коробок розподілена нормально)?
В
умовах задачі параметр а
= 1,06, параметр
-невідомий.
Розглянемо випадкову величину (
- маса коробок. Потрібно визначити
p
(
> 0,94), тобто p (
> 0,94) = p (0,94 <
< + ∞)
З
таблиці Додатка
2 визначимо
,за формулою
(14) маємо
=
1-
, тоді p (0,94 <
< + ∞)
1-1+
=
.
Параметр
знайдемо з умови р (
< 1) = 0,5
тобто
1-
звідки одержимо
)
= 0,95.
За
таблицею Додатка 3 визначимо
= 1,645, тоді з рівності
знайдемо значення
.
Остаточно одержимо
.