Випадкові події Стохастичний експеримент, простір елементарних наслідків

Вихідними поняттями теорії ймовірностей є поняття стохастичного експерименту, випадкової події та імовірності випадкової події. Стохастичними називаються експерименти, можливі наслідки яких відомі, але заздалегідь угадати, який з них буде мати місце не можна. Множину всіх можливих наслідків експерименту називають простором елементарних наслідків і позначають =.

Таким чином, розглянутому експерименту поставлена у відповідність деяка множина , елементами якої є взаємовиключні елементарнінаслідки . Результатом експерименту є один і тільки один результат. Розглянемо приклади.

1. Один раз кидають монету. Множина , де буква Г означає появу герба, буква Р-поява решки.

2. Один раз кидають гральний кубик. Можливі наслідки цього експерименту - випадання числа очок, рівного 1, 2, 3, 4, 5, 6, тобто

= {1, 2, 3, 4, 5, 6} .

3. Монету кидають двічі,

,

тут ГГ означає , що обидва рази з'явиться герб,

ГР- при першому киданні з'явиться герб, а при другому -решка,

РГ- при першому киданні з'явиться решка, при другому -герб,

РР- обидва рази з'явиться решка.

4. Монету кидають до першої появи герба. Можливі наслідки експерименту:

Г- герб випаде з першого разу,

РГ- герб випаде при другому киданні,

РРГ- герб випаде при третьому киданні і т. д

Теоретично експеримент може тривати нескінченно довго. Простором елементарних подій такого експерименту є нескінченна множина

5. Дві особи А і В умовилися зустрітися в інтервалі часу [0,T]. Позначимо

x - час приходу особи А_,

_{Y -} час приходу особи В.

Геометрично цей простір представляє квадрат, зображений на Рисунок.1

Рисунок 1. Простір елементарних наслідків експерименту 4.

Множину називають простором елементарнихнаслідків (подій). Наведені приклади показують, що множина може бути дискретною і неперервною. До дискретних відносяться скінченні або зліченні множини елементарних наслідків, до неперервних - множини типу континуума (будь-який скінченний або нескінченний інтервал на числовій прямій являє приклад множини типу континуума ).

Простір елементарних наслідків залежить від умов, в яких відбувається випадковий експеримент. Надалі будемо розглядати умови, за яких наслідки експерименту рівно можливі, тобто ніякий результат експерименту не має об'єктивної переваги перед іншими.

У розглянутих вище прикладах передбачається, що експерименти відбуваються в ідеальних умовах (ідеальна монета кидається на ідеально гладку поверхню й т.д.).

Визначення випадкової події.

Елементарні наслідки експерименту - це найпростіші випадкові події й визначенню не підлягають. Однак у кожному випадковому експерименті крім елементарних можуть відбуватися й інші випадкові події . Так, наприклад, у прикладі 2 можна розглянути події:

А - випадання парного числа очок,

В - випадання числа очок, не менше 4,

С - випадання непарного числа очок і т.д.

Подія А відбудеться, якщо буде мати місце один з наслідків експерименту: випаде число очок, рівне 2 або 4 або 6. Таким чином,

А = {2, 4, 6} , В = {4, 5, 6}, C = {1, 3, 5} .

У прикладі 3 можуть відбутися події:

А - хоча б один раз випаде герб,

В - герб випаде при першому киданні,

С - хоча б один раз випаде решка і т.д.

А = {ГГ, ГР, РГ}, В = {ГГ,ГР}, С = {РР,РГ,ГР}.

Нехай у прикладі 4 подія А полягає в тому, що буде зроблено не більше трьох кидань. Тоді

А = .

Розглянемо задачу про зустріч (приклад 5). Припустимо, що кожна з осіб А и В очікує іншого час, не більш ніж t ,<t <Т. Нехай С - подія, яка полягає в тому, що зустріч відбудеться. Тоді

С ={(x, y) : }

(Рисунок 2) .

Рисунок 2. Подія С- зустріч відбудеться

Ті елементарні наслідки, за яких подія А настає, називають сприятливими події А.

Отже, випадкова подія А – це деяка підмножина , що складається із всіх тих елементів- елементарних подій, які сприяють події А.

Лекція 2 .

Алгебра подій .

Подія називається неможливою, якщо вона в експерименті напевно не наступить і позначається Подія називаєтьсядостовірною, якщо вона в експерименті напевно наступить і позначається . Сама множинає достовірною подією, оскільки один з його наслідків обов'язково відбудеться. Так , у прикладі 2 подія - « випадіння числа очок, рівного 7», є в цьому випадку неможливою , а подія - «випадання числа очок, не більше 6», - достовірна подія.

Якщо у випадковому експерименті з настання події А випливає настання події В, то говорять, що А тягне за собою В( АВ ).

Якщо А В , а ВА, то говорять , що події А и В рівносильні ( А = В ).

Сумою двох подій А и В називають подію А + В (АВ), що відбувається тоді й тільки тоді, коли відбувається або подія А , або подія В. Сума подій відповідає об'єднанню множин (Рисунок 3).

Рисунок 3. Сума двох подій.

У Прикладі 2 А + В= { 2, 4, 5, 6}.

Аналогічний зміст має сума будь-якого числа подій. Якщо I-довільна множина значень деякого індексу i, A- деяка множина подій то сума є подію , що відбувається тоді й тільки тоді, коли відбувається хоча б одна подія A.

Добутком двох подій А и B (подій A, i) називають подію AВ (АВ), що відбувається тоді й тільки тоді, коли відбувається й подія А, і подія В ( всі події A, i) .

Добуток подій відповідає перетину множин (Рисунок 4).

Рисунок 4. Добуток двох подій.

Для подій із приклада 2 АВ = { 4, 6 }.

Різниця А \ В двох подій А и В є подія, що відбувається тоді й тільки тоді. коли відбувається А , але не відбувається В. Різниця подій відповідає різниці множин (Рисунок 5)

Рисунок 5. Різниця двух подій.

У прикладі 2 А \ В = {2}.

Подія називаєтьсяпротилежною події А, якщо воно відбувається тоді й тільки тоді, коли не відбувається А (відповідає доповненню множин) Рисунок 6.

Рисунок.6. Протилежна подія.

У прикладі 2 = {1, 3, 5 }.

Операції додавання й множення подій мають наступні властивості :

а) А+В = В+А , АВ = ВА (комутативність);

б) (А+В)+С =А+(В+С) , А(ВС)=(АВ)С (асоциативність);

в) (А+В)С=АС+ВС) (дистрибутивність множення відносно додавання).

Відзначимо ще деякі очевидні співвідношення:

А, А,,.

Дві події А і В називаються неспільними, якщо неможливо їхнє спільне наставання, іншими словами АВ = . Прикладом неспільних подій є А и.

Сукупність подій А,А, … , Астановитьповну групу попарно несумісних подій , якщо:

1. хоча б одна із цих подій неодмінно відбувається;

2. будь-яка пара подій несумісна , АА=,i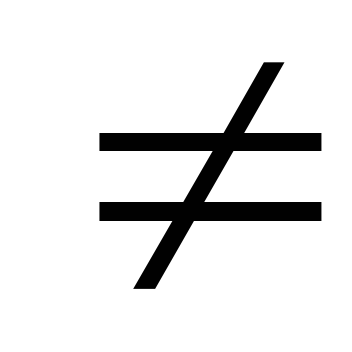j, i,j=.

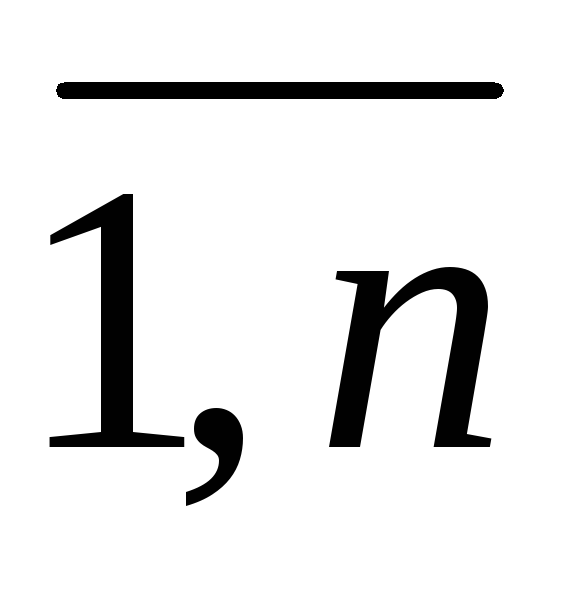Класичне означення ймовірності.

Імовірність - це кількісна оцінка можливості настання випадкової події. За класичним означенням, імовірністю випадкової події Р(А) називається відношення числа m сприятливих наслідків до загального числа n рівноможливих наслідків експерименту

Р(А) =

Класична ймовірність має наступні властивості:

1. Р(А)0.

2. Імовірність достовірної події дорівнює 1:

Р()=1.

3. Якщо подія С = А+В, причому А и В несумісні, то

Р(С) = Р(А)+Р(В).

4. Імовірність протилежної події дорівнює

Р()=1- Р(А).

5. Імовірність неможливої події дорівнює нулю

Р() = 0.

5. Якщо АВ, то Р(А)Р(В).

6. Імовірність будь-якої події міститься між нулем і одиницею

0Р(А)1.

Розглянемо приклади на обчислення ймовірностей.

Приклад 1. Один раз підкидають монету. Чому дорівнює ймовірність випадання герба?

Тут , причому наслідки експерименту рівно можливі , А={Г} , у такий спосіб m=1, n=2, P(A) = .

Приклад 2. Один раз підкидають гральний кубик. Чому дорівнює ймовірність того, що випаде число очок, не менш чотирьох ?

- рівноможливі, А={4,5,6}, m=3, n=6, P(A) = .

У більш складних задачах не представляється можливим явно записати всі наслідки експерименту, а також сприятливі випадковій події наслідки. У таких випадках застосовуються комбінаторні методи підрахунку чисел m і n.

Приклад 3. У ящику знаходиться 10 деталей, серед яких 3 бракованих. З ящика навмання витягають 5 деталей. Знайти ймовірність того, що серед них виявиться дві браковані.

Подія А - серед 5-ти витягнутих деталей 2 бракованих, а 3 якісних.

Для підрахунку m і n використаємо правило сполучень:

n =, P(A) ===.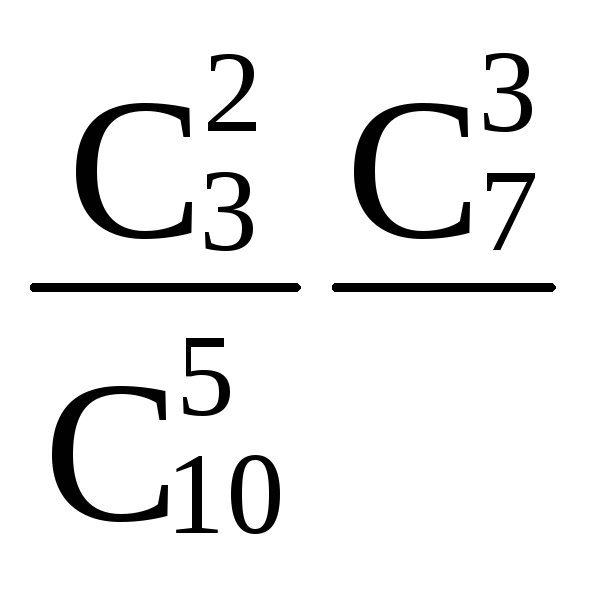

Відзначимо недоліки класичного означення ймовірностей:

1. Класичне означення неможливо застосувати у випадку нескінченного простору елементарних наслідків.

2. Існує проблема знаходження розумного способу виділення «рівноможливих випадків». Наприклад, як визначити ймовірність того, що народжена дитина виявиться хлопчиком?

По мірі розвитку теорії ймовірностей з'явилися інші означення ймовірності, які усували недоліки класичного. Розглянемо ще один підхід до означення ймовірності.

Статистична оцінка ймовірності.

Тривалі спостереження над появою або не появою події А при великій кількості незалежних випробувань у ряді випадків показують, що число появ події А підкоряється стійким закономірностям. Позначимо

- число появ події А,

n - число випробувань,

- частота появи події А при досить великому n зберігає майже постійну величину.

Таким чином, під статистичною ймовірністю розуміється відносна частота появи події А в n зроблених експериментах.

Статистична ймовірність має ті ж властивості, що й класична ймовірність, але при цьому не потрібно рівно можливості наслідків . Найбільш загальним є аксіоматичне оизначення ймовірності, що сформулював радянський математик Колмогоров А.Н. в 1933 р. Однак розгляд цього означення виходить за рамки даного курсу лекцій.

Лекції 3,4.