Тема 6. Перевірка гіпотези про розподіл за критерієм (хі-квадрат). Завдання 6

Ціль завдання – освоїти процедуру обчислень при вивченні закону розподілу випадкової величини .

Зміст завдання. По даному статистичному ряді:

1. Побудувати гістограму частот.

2. Сформулювати гіпотезу й види розподілу.

3. Знайти оцінки параметрів розподілу.

4. На рівні значимості = 0,05 перевірити гіпотезу про розподіл випадкової величини.

Всі проміжні обчислення поміщати у відповідні таблиці. Варіанти наведені в Таблиці 15.

Приклад виконання завдання.

Номер інтервалу i	Границі інтервалу	Частота m
1	14 - 23	2
2	23 - 32	3
3	32 -41	6
4	41 -50	17
5	50 -59	10
6	59 -68	9
7	68 -77	3

Розглянемо вибірку, у нагляді статистичного ряду, наведеного в Таблиці 11.

Таблиця 11. Статистичний ряд.

. Перевіримо на рівні значущості = 0,1 гіпотезу про нормальний розподіл вибірки. Побудуємо гістограму частот.

Рисунок 5. Гістограма частот.

Обчислимо спочатку оцінку математичного сподівання й оцінку дисперсії, для цього складемо Таблицю 12.

Таблиця 12. Допоміжні обчислення, для оцінки математичного сподівання й оцінки дисперсії

Номер інтервалу i	Границі інтервалу	Середина інтервалу x	Частота m	xm	xm
1	14 – 23	18,5	2	37,0	684,50
2	23 – 32	27.5	3	82,5	2268,75
3	32 -41	31,5	6	219,0	7993,50
4	41 -50	45,5	17	773,5	35194,25
5	50 -59	54,5	10	545,0	29702,50
6	59 -68	63,5	9	571,5	36290,25
7	68 -77	72,5	3	217,5	15768,75
	-	-	50	2453,0	127902,50

n = = 50 , k = 7 ,=== 49,06

==

= = 12,30

Ймовірності = P() обчислимо за формулою

= P()=, i=1,2,..,7,

де - відповідно нижня й верхня границі інтервалів, а значенняберуться з таблиці Додатка 2.

Складемо нову Таблицю 13, розширивши перший і останній інтервали.

Таблиця 13. Обчислення ймовірностей = P()

Номер інтер- валу i	Границі інтервалу	Частота m
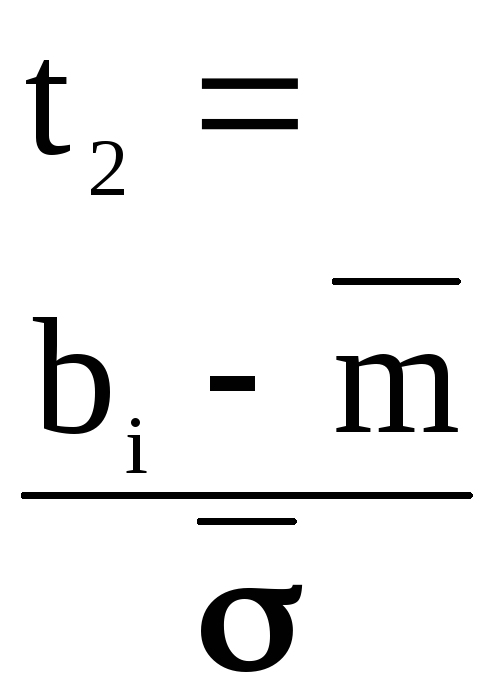
1	- 23	2		-2,12	0	0,0170	0,0170
2	23 – 32	3	-2,12	-1,39	0,017	0,0823	0,0653
3	32 -41	6	-1,39	-0,66	0,0823	0,2546	0,1723
4	41 -50	17	-0,66	0,08	0,2546	0,5319	0,2773
5	50 -59	10	0,08	0,81	0,5319	0,7910	0,2591
6	59 -68	9	0,81	1,54	0,7910	0,9382	0,1472
7	68 -	3	1,54		0,9382	1	0,0618

Обчислимо вибірково значення статистики по формулі

Для обчислення складемо ще одну таблицю , об’єднуючи при цьому перший інтервал із другим і сьомий інтервалом із шостим.

Таблиця 14.Обчислення

Номер інтер- валу i		n
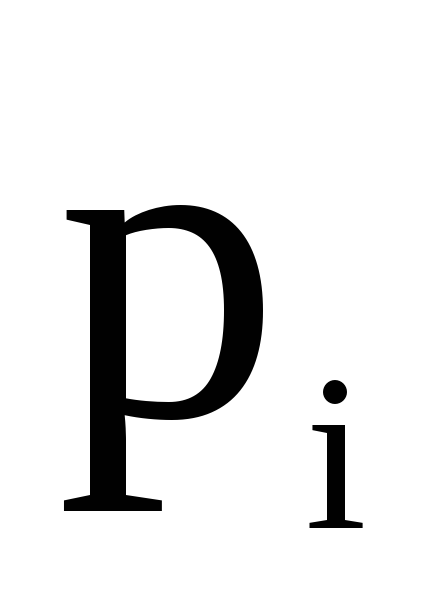
1 2	0,0823	4,1154	5	0,25
3	0,1723	8,6159	6	1,00
4	0,2773	13,86514	17	0,64
5	0,2591	12,95513	10	0,69
6 7	0,2090	10,45010	12	0,40
Сума				2,98

Сума чисел остатнього стовпця є вибіркове значення критерію, = 2,98. За таблицею квантилей розподілу знайдемо . Після об’єднання , число інтервалів k=5, число параметрів нормального розподілу r=2,. Тоді== 4,61. Вибіркове значення статистики критерію дорівнює 2,98 і це значення менше, ніж=0,64, отже гіпотеза про нормальний розподіл вибірки приймається.