Тема 2. Випадкові величини. Функція розподілу випадкової величини.

Числові характеристики випадкових величин.

Завдання № 2

Ціль завдання – закріплення знань основних понять , що стосуються дискретних і неперервних випадкових величин. Придбання навичок у рішенні практичних завдань по побудові функції розподілу й обчисленню математичного сподівання й дисперсії.

Завдання містить дві задачі. Варіанти наведені в Таблиці 3.

Задача 1. Виробляються послідовні незалежні випробування N приладів на надійність. Кожний наступний прилад випробовується тільки в тому випадку, якщо попередній виявився надійним. Імовірність витримати випробування для кожного приладу дорівнює p . Знайти:

а) ряд розподілу випадкового числа випробуваних приладів;

б) функцію розподілу й побудувати її графік;

в) математичне очікування й дисперсію.

Задача 2. Щільність розподілу ймовірностей задана таким способом:

f(x) =

Обчислити:

а) коефіцієнт А ;

б) функцію розподілу ;

в) математичне очікування й дисперсію;

г) імовірність того, що випадкова величина прийме значення з

інтервалу ( ).

Приклад виконання завдання.

1. Розв’яжемо задачу при N = 3, p = 0,8.

а) Дискретна випадкова величина - число випробуваних приладів. Можливі значення цієї випадкової величини :Знайдемо ймовірності цих значень. Позначимо події:- i-ий випробуваний прилад виявився надійним,- i-ий випробуваний прилад виявився ненадійним. Тоді

= P(=1) =P() = 1- 0,8 = 0,2,

= P(=2) =P() = 0,8· 0,2 =0,16,

= P(=3) =P() = 0,8·0,8·0,2 + 0,8· 0,8·0,8 = 0,64.

Закон розподілу має вигляд (Таблиця 2):

Таблиця 2. Закон розподілу дискретної випадкової величини.

	1	2	3
	0,2	0,16	0,64

б) Функцією розподілу F(x), яка визначена для будь-якого дійсного x, називається ймовірність того, що випадкова величина  прийме значення менше x, тобто де. Оскільки функція F(x) визначена для всіх дійсних значень x, то розглянемо послідовно інтервали:

1) х  (- ∞, 1], F (x) = P ( < x) = 0, тому що подія ( < x) для такого x є неможливою подією.

2) х  (1, 2], F (x) = P( = 1) = 0,2 , тут нерівності  < x задовольняє єдине значення  = 1

3) х  (2, 3], F (x) = P( = 1) + P ( = 2) = 0,2 + 0,16 = 0,36 , тут нерівності  < x задовольняють два значення  = 1 і  = 2.

4) x (3, ), F (x) = P( = 1) + P ( = 2) + P ( = 3) = 0,2 + 0,16 + 0,64 = 1, тут нерівності  < x задовольняють всі значення . Таким чином,

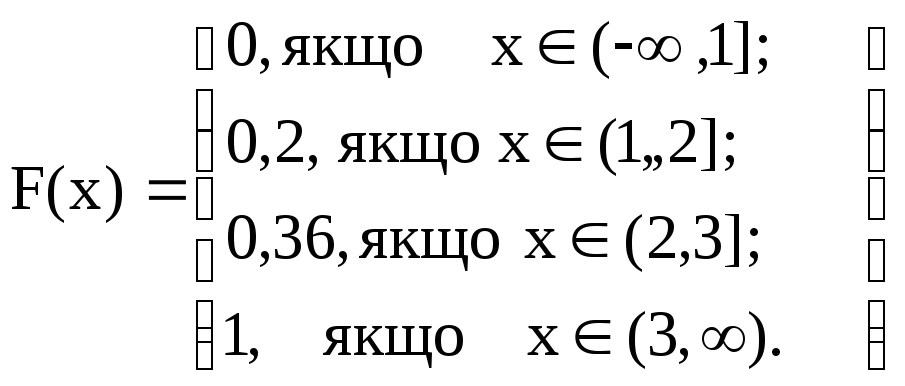
График функції розподілу наведен на Рисунку 1.

Рисунок 1. Графік розподілу випадкової величини Задачи 1..

в) Знайдемо математичне сподівання та дисперсію.

=1· 0,2 + 2 · 0,16 + 3 · 0,64 = 2,44,

1· 0,2 + 4 · 0,16 + 9 · 0,64 - (2,44)² = 0,6464.

2. Випадкова величина розподілена за законом , який обумовлений щільністю розподілу ймовірностей виду

f (x) =

Знайти параметр a, F(x), M () , D() .

Параметр a знайдемо із властивості , інтегралрозіб'ємо на суму трьох інтегралів

Намалюємо графік щільності розподілу f (x) (Рисунок 2)

Рисунок 2. Графік щільності розподілу f (x)

Обчислимо функцію розподілу, для цього розглянемо інтервали .

1. х  (- ∞, 0) ,

2. х  [0, 2] ,

3. х (2,) .

Графік функції наведений на Рисунку 3.

Обчислимо математичне сподівання й дисперсію:

Рисунок 3. Графік функції розподілу неперервної випадкової величини.